
2007-2008学年度淄川第二学期初三期末考试
数学试卷
一、精心选一选(本题共13小题,在每小题所给出的四个选项中。只有一个是正确的,请选出你认为唯一正确的答案,每小题3分,计39分).
1.下列函数表达式中,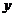 不是
不是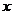 的反比例函数的是 ( )
的反比例函数的是 ( )
A.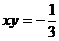 B.
B.
C.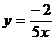 D.
D. (
(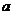 为常数,
为常数,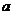 ≠0)
≠0)
2.方程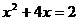 的正根为 ( )
的正根为 ( )
A.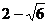 B.2+
B.2+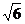 C.
C.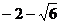 D.
D.
3.下列命题中,假命题是 ( )
A.一条直角边和另一条直角边上的中线对应相等的两个直角三角形全等
B.两条直角边对应相等的两个直角三角形全等
C.两个锐角对应相等的两个直角三角形全等
D.斜边及一锐角对应相等的两个直角三角形全等
4.小明和小亮的口袋里都装有五张不同的2008 北京奥运会福娃纪念卡,小明从口袋里摸出一张福娃贝贝,小亮从口袋里摸出一张福娃也是贝贝的概率是 ( )

A.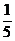 B.
B.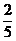 C.
C.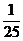 D.
D.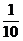
5.已知四边形ABCD中,∠A=∠B=∠C=90°,如果再添加一个条件,即可推出该四边形是正方形。那么这个条件可以是 ( )
A.∠D=90° B.BC=CD C.AD=BC D.AB=CD
6.在淄川区开展的读书节活动中,某学校购进4000本相同开本的图书,有数学类图书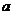 本.今分10次各抽取100本图书进行抽查,平均有数学类图书20本.对
本.今分10次各抽取100本图书进行抽查,平均有数学类图书20本.对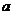 的叙述正确的是 ( )
的叙述正确的是 ( )
A.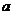 =800 B.
=800 B.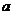 ≠800
≠800
C.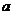 的值应在800左右 D.无法确定
的值应在800左右 D.无法确定
7.如图,在周长为
A.
8.矩形和等腰梯形共有的性质是 ( )
A.对角线互相平分 B.对边平行 C.对角线相等 D.对角相等
9.下列一元二次方程中,没有实数根的方程是 ( )
A.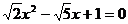 B.
B.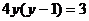
C.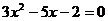 D.
D.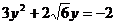
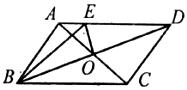
10.已知:如图,AB=CD,BE=DF,∠B=∠D.则下列结论:
①AE=CF;②∠AFE=∠CEF:③△ABF≌△CDE;④四边形AECF是平行四边形.其中结论正确的有 ( )
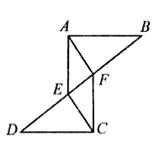
A.4个 B.3个 C.2个 D.1个
11.如图,在△ABC中,∠ACB=90°,CD⊥AB于D,CE是AB边上的中线,∠BCD=3∠DCA,图中与∠3相等的角是 ( )
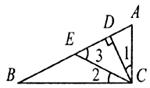
A.∠1 B.∠
12.若关于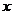 的一元二次方程
的一元二次方程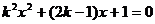 有实数根,则下列结论正确的是
( )
有实数根,则下列结论正确的是
( )
A.当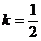 时方程两根互为相反数 B.当
时方程两根互为相反数 B.当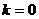 时方程的根是
时方程的根是
C.当 =±1时方程两根互为倒数 D.当
=±1时方程两根互为倒数 D.当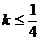 且
且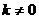 时方程有实数根
时方程有实数根
13.已知平面直角坐标系中的点M(2,1),N(2,6),反比例函数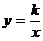 与线段MN相交,过反比例函数
与线段MN相交,过反比例函数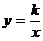 上任意一点P作
上任意一点P作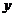 轴的垂线JPG,G为垂足,O为坐标原点,则△OPG的面积S的取值范围是 ( )
轴的垂线JPG,G为垂足,O为坐标原点,则△OPG的面积S的取值范围是 ( )
A.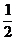 ≤S≤3
B.1≤S≤
≤S≤3
B.1≤S≤
二、细心填一填(本题共7小题,满分28分,只要求填写最后结果,每小题填对得4分).
14.把方程 写成
写成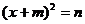 的形式,则
的形式,则 = ,
= ,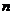 = .
= .
15.平面直角坐标系中有六个点:A(1,5),B(-3,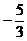 ),C(-5,-1),D(-2,
),C(-5,-1),D(-2,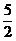 ), E(3,
), E(3,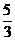 ),F(
),F(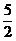 ,2),其中有五个点在同一个反比例函数的图象上,那么不在这个反比例函数图象上的点是
.
,2),其中有五个点在同一个反比例函数的图象上,那么不在这个反比例函数图象上的点是
.
16.连掷两个均匀的小立方体(每个面上分别标有1,2,3,4,5,6),它们朝上的数字 相同的概率是 .
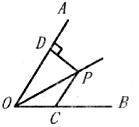
17.如图,点P是△AOB的角平分线上的一点,过P作交OB于点C.若∠AOB=60°,OC=4,则点P到OA的距离PD等于 。
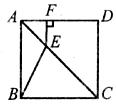
18.如图,E是正方形ABCD的对角线AC上的点,EF⊥AD,F是垂足,EF=6,BE=10,则正方形ABCD的面积为 .
19.如图,在梯形ABCD中,AD//BC,CD⊥BC,∠B=60°,AD=CD=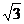 cm,则梯形的中位线EF的长为
cm.
cm,则梯形的中位线EF的长为
cm.

20.若一元二次方程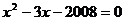 的两实数根分别为
的两实数根分别为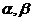 ,则代数式
,则代数式 的值是
.
的值是
.
三、耐心做一做,相信你能写出正确的解答过程(共53分,注意审题要细心,书写要规范和解答要完整).
21.完成下列各题(本题满分24分,每小题6分)
(1)解方程: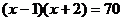 .
.
(2)解方程: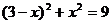 .
.
(3)在摸牌游戏中,如果每组3张牌,它们的牌面数字分别是1,2,3,那么从每组牌中各随机摸出一张牌,两张牌牌面数字的和为几的概率最大?最大的概率是多少?通过树状图或表格说明.
(4)已知关于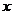 的一元二次方程
的一元二次方程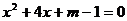 .
.
①请你为 选取一个合适的整数,使得到的方程有两个不相等的实数根:
选取一个合适的整数,使得到的方程有两个不相等的实数根:
②设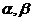 是(1)中你所得到的方程的两个实数根,求
是(1)中你所得到的方程的两个实数根,求 的值.
的值.
22.(本题满分6分)
已知:如图,在菱形ABCD中,∠A=72°,请你设计三种不同的方案,将菱形ABCD分割成四个三角形,使每个三角形都是等腰三角形.(画图工具不限,要求画出分割线段;标出每个三角形各内角的度数)'两种分割方案只要有一条分割线不同就认为是两种不同的分割方案.
23.(本题满分7分)
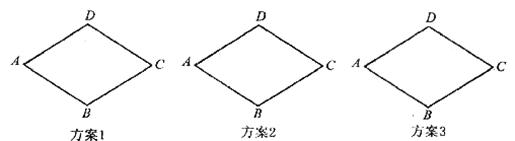
已知:如图,在△ABD中,AC⊥BD,垂足为点C,BE与AC相交于点F,且AC=BC,CD=CF.
求证:(1)∠DBF=∠CAD;(2)BE⊥AD.
24.(本题满分8分)
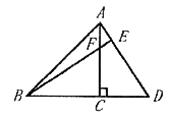
如图,点M是矩形ABCD的边AD的中点,点P是BC边上的一个动点.PE⊥MC,PF⊥BM,垂足分别为E,F.
(1)当矩形的长与宽满足什么条件时,四边形PEMF为矩形?猜想并证明;
(2)在(1)的条件下,当点P运动到什么位置时,矩形PEMF变为正方形,并证明.
25.(本题满分8分)
已知:如图,点(1,3)在函数 的图象上。矩形ABCD的边BC在
的图象上。矩形ABCD的边BC在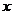 轴上.E是对角线BD的中点,函数
轴上.E是对角线BD的中点,函数 的图象经过A,E两点,点E的横坐标为m.
的图象经过A,E两点,点E的横坐标为m.
(1)求 的值;
的值;
(2)求点C的横坐标(用含 的代数式表示);
的代数式表示);
(3)当∠ABD=45°时,求m的值.


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com