
2007-2008学年度第二学期八年级期中质量检测
数学试卷
一、选择题:(3分×10=30分)
1.已知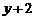 与
与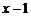 成正比例,且
成正比例,且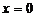 时,
时,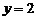 ,则
,则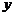 与
与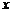 的函数关系式是( ).
的函数关系式是( ).
A.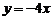 B.
B.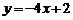 C.
C.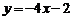 D.
D.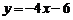
2.如图,已知,AC平分∠PAQ,点B、B′分别在AP、AQ上,如果添加一个条件,即可推出AB=AB′,那么这个条件不可以是( ).
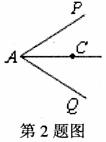
A.BB′⊥AC B.∠ABC=∠AB′C C.∠ACB=∠ACB′ D.BC=B′C
3.已知函数:①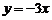 ;②
;②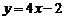 ;③
;③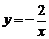 ;④
;④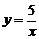 ,当
,当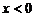 时,
时,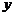 随
随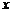 的增大而减小的函数是( ).
的增大而减小的函数是( ).
A.①② B.①④ C.②③ D.②④
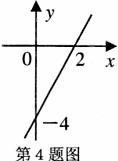
4.已知一次函数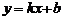 图象如图所示,当
图象如图所示,当 时,
时,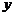 的取值范围是( ).
的取值范围是( ).
A.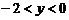 B.
B.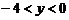 C.
C.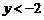 D.
D.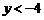
5.如图,小手盖住的点的坐标可能为( ).
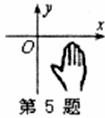
A.(5,2) B.(―6,3) C.(―4,―6) D.(3,―4)
6.打开某洗衣机开关,在洗涤衣服时(洗衣机内无水),洗衣机经历了进水、清洗、排水、脱水四个连续过程,其中进水、清洗、排水时洗衣机中的水量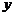 (升)与时间
(升)与时间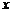 (分钟)之间满足某种函数关系,其函数图象大致为( ).
(分钟)之间满足某种函数关系,其函数图象大致为( ).
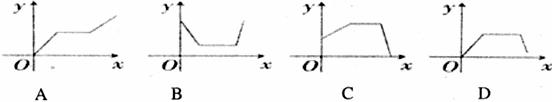
7.如图,在△ABC中,BC=
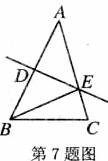
A.
8.两条直线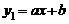 与
与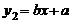 在同一直角坐标系中的图象可能是( )
在同一直角坐标系中的图象可能是( )

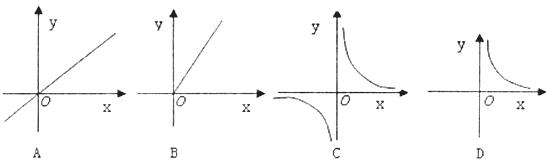
9.一矩形的面积是8,则这个矩形的一组邻边长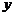 与
与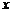 的函数关系的图像大致是( ).
的函数关系的图像大致是( ).
10.在平面直角坐标系中,平行四边形ABCD的顶点A、B、D的坐标分别是(0,0),(5,0),(2,3),则顶点C的坐标是( ).
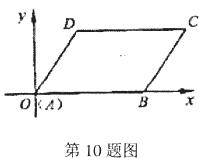
A.(3,7) B.(5,3) C.(7,3) D.(8,2)
二、填空题:(3分×10=30分)
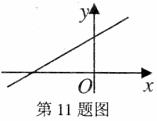
11.已知一次函数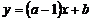 的图象如图所示,那么a的取值范围是________.
的图象如图所示,那么a的取值范围是________.
12.在平面直角坐标中,点A(2,―3)关于原点对称的点的坐标是________.
13.在函数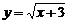 中,自变量
中,自变量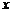 的取值范围是________.
的取值范围是________.
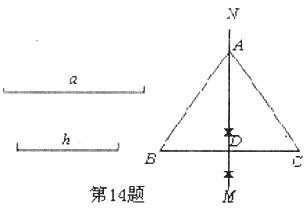
14.如图,已知线段a、h,作等腰△ABC,使AB=AC,且BC=a,BC边上的高AD=h.张红的作法是:(1)作线段BC=a;(2)作线段BC的垂直平分线MN,MN与BC相交于点D;(3)在直线MN上截取线段h;(4)连结AB,AC,△ABC为所求的等腰三角形.上述作法的四个步骤中,有错误的一步你认为是________.(填步骤序号.)
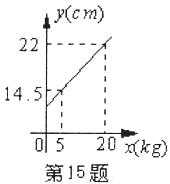
15.如图,弹簧总长 (cm)与所挂物体质量
(cm)与所挂物体质量 (kg)之间是一次函数关系,则该弹簧不挂物体时的长度为________cm.
(kg)之间是一次函数关系,则该弹簧不挂物体时的长度为________cm.
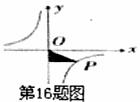
16.如图,P是双曲线上的一点,且图中的阴影部分的面积为5,则此反比例函数的解析式为________.
17.下列有关命题、公理、定理的说法:(1)公理是命题; (2)定理是由公理或其它定理定义推出的正确的命题; (3)真命题是公理; (4)命题是被证明是正确的公 理.正确的有________.(填序号.)
18.从地面到高空11千米之间,气温随着高度的升高而下降,每升高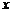 千米
千米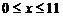 处的气温为
处的气温为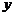 ℃,则
℃,则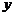 与
与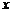 的函数关系是________.
的函数关系是________.
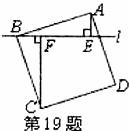
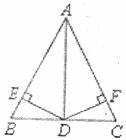
19.如图,过正方形A曰CD的顶点B作直线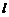 ,过A、C作
,过A、C作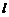 的垂线,垂足分别为E、F.若AE=1,CF=3,则AB的长度为________.
的垂线,垂足分别为E、F.若AE=1,CF=3,则AB的长度为________.
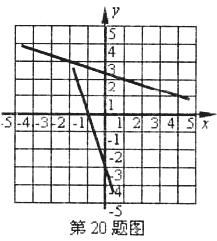
20.如图,是在同一坐标系内作出的一次函数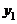 、
、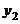 的图象
的图象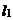 、
、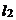 ,设
,设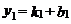 ,
,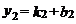 ,则方程组
,则方程组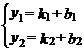 的解是________.
的解是________.
三、解答题(本题共7小题,共60分.要求证明过程中重要依据要写出)
21.(本题满分8分)
如图,已知△ABC为等边三角形,D、E、F分别在边BC、CA、AB上,且△DEF也是等边三角形.除已知相等的边以外请你猜想还有哪些相等线段,并证明你的猜想是正确的;
22.(本题满分8分)
某产品每件成本10元,试销阶段每件产品的销售价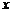 (元)与产品的日销量
(元)与产品的日销量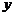 (件)之间的关系如下表:
(件)之间的关系如下表:
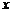 (元)
(元)
15
20
25
……
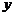 (件)
(件)
25
20
15
……
若日销售量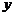 是销售价
是销售价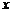 的一次函数.
的一次函数.
(1)求出日销售量 (件)与销售价
(件)与销售价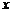 (元)的函数关系式;
(元)的函数关系式;
(2)求销售价定为30元时,每日的销售利润.
23.(本题满分8分)
我们知道,两边及其中一边的对角分别对应相等的两个三角形不一定全等.那么在什么情况下,它们会全等?
24.(本题满分8分)
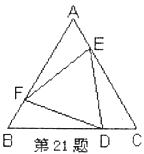
如图,在△ABC中,AB=AC,D是BC的中点,连接AD.DE⊥AB,DF⊥AC,E、F是垂足.图中共有多少对全等三角形?请直接用“≌”符号把它们分别表示出来.并选出其中一组加以证明。
25.(本题满分8分)
如图,已知直线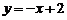 与
与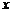 轴、
轴、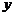 轴分别交于点A和点B,
轴分别交于点A和点B,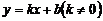 经过点C(1,0),且把△AOB分成两部分,若△AOB被分成的两部分面积相等,求k和b的值.
经过点C(1,0),且把△AOB分成两部分,若△AOB被分成的两部分面积相等,求k和b的值.
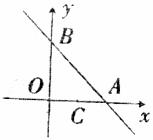
26.(本题满分8分)
如图,已知△ADF和△BCE中,∠A=∠B,点D、E、F、C在同一直线上,有如下三个关系式:①AD=BC;②DE=CF;③BE∥AF.
(1)请用其中两个关系式作为条件,另一个作为结论,写出所有你认为正确的命题.(用序号写出命题,书写形式如:如果①、②,那么③)
(2)选择(1)中你写出的一个命题,说明它正确的理由.
27.(本题满分12分)
为了预防一种流行性传染病,某学校对教室采用药熏消毒法进行消毒,如图所示,已知药物燃烧时,室内每立方米空气中的含药量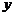 (mg)与时间
(mg)与时间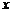 (min)成正比例,药物燃烧完成后,
(min)成正比例,药物燃烧完成后,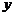 与
与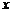 成反比例.现测得药物8min燃毕,此时室内空气中每立方米的含药量为6mg.请根据题中所提供的信息,解答下列问题:
成反比例.现测得药物8min燃毕,此时室内空气中每立方米的含药量为6mg.请根据题中所提供的信息,解答下列问题:

(1)药物燃烧时,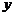 关于
关于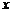 的函数关系式为________,自变量
的函数关系式为________,自变量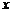 的取值范围是________;药物燃烧完后,
的取值范围是________;药物燃烧完后,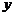 关于
关于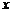 的函数关系式为________.
的函数关系式为________.
(2)研究表明,当空气中每立方米的含药量低于1.6mg时学生方可进教室,那么从消毒开始,至少需要经过________min后,学生才能回到教室;
(3)研究表明,当空气中每立方米的含药量不低于3mg且持续时间不低于10min时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com