
2008-2009学年度荆州市公安县第一学期九年级期中考试
数学试卷
满分120分,考试时间120分钟
第Ⅰ卷
一、选择题(共30分)
1.下列式子总有意义的是
A.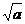 B.
B.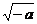 C.
C.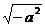 D.
D.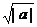
2.在二次根式①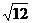 、②
、②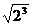 、③
、③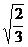 、④
、④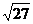 中与
中与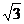 是同类二次根式的是
是同类二次根式的是
A.①和③ B.②和③ C.①和④ D.③和④
3.若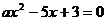 是一元二次方程,则不等式3
是一元二次方程,则不等式3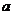 +6>0的解集是
+6>0的解集是
A.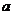 >―2 B.
>―2 B.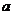 <―
<―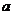 >一2且
>一2且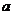 ≠0 D.
≠0 D.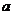 >
>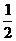
4.已知一元二次方程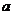
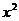 +b
+b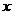 +c=0中二次项系数、一次项系数和常数项之和为零,那么方程必有一根为
+c=0中二次项系数、一次项系数和常数项之和为零,那么方程必有一根为
A.0 B.
5.观察下列用纸折叠成的图案,如下图所示。其中轴对称图形和中心对称图形的个数分别为
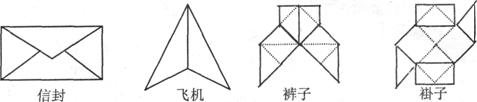
A.3、l B.2、
6.等腰三角形的底和腰是方程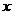 2―6
2―6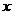 +8=0的两根,则这个三角形的周长为
+8=0的两根,则这个三角形的周长为
A.8 B.
7.如下图,将△ABC绕着点C按顺时针方向旋转20°,B点落在B’位置,A点落在A’位置,若AC⊥A’B’,则∠BAC的度数是
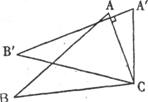
A.50° B.60° C.70° D.80°
8.如下图,⊙O的直径CD过弦EF的中点G,∠EOD=40°,则∠DCF等于
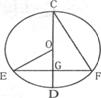
A.80° B.50° C.40° D.20°
9.如下图,8×8方格纸上的两条对称轴EF、MN相交于中心点O,对△ABC分别作下列变换:
①先以点A为中心顺时针方向旋转90°,再向右平移4格、向上平移4格;
②先以点O为中心作中心对称图形,再以点A的对应点为中心逆时针方向旋转90°;
③先以直线MN为轴作轴对称图形,再向上平移4格,再以点A的对应点为中心顺时针方向旋转90°,其中,能将△ABC变换成△PQR的是
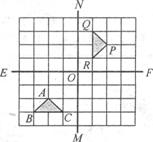
A.①② B.①③ C.②③ D.①②③
10.圆O的半径为
A.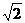 cm B.8
cm B.8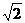 cm C.6
cm C.6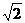 cm D.12cm
cm D.12cm
二、填空题(共l8分)
11.式子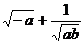 有意义,则点P(
有意义,则点P(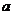 ,b)在_______________象限.
,b)在_______________象限.
12.若方程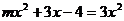 是关于
是关于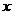 的一元二次方程,则m的取值范围是__________.
的一元二次方程,则m的取值范围是__________.
13.一种产品,原来每件售价是81元,由于求大于供,所以产品连续两次涨价,现售价是100元,则平均每次的增长率为__________. (精确到0.1个百分点)
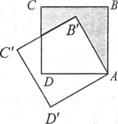
14.如下图,边长为l的正方形ABCD绕点A逆时针旋转30°到正方形A’B’C’D’,图中阴影部分的面积为_________.
15.定义运算“@”的运算法则为: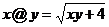 ,则 (2@6)@8=_________.
,则 (2@6)@8=_________.
16.已知,如下图:AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=45°。给出以下四个结论:①∠EBC=22.5°;②BD=DC;③劣弧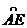 是劣弧
是劣弧 的2倍;④AE=BC。其中正确结论的序号是_________。
的2倍;④AE=BC。其中正确结论的序号是_________。
第Ⅱ卷
三、解答题(共72分)
17.(本题共两小题,每小题5分,满分l0分)
(1)计算: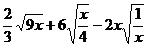
(2)解方程:(3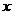 +2)(
+2)(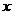 +3)=
+3)=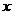 +14
+14
18.(6分)已知:(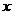 ―15)2=169,(y―1)3= ―0.125
―15)2=169,(y―1)3= ―0.125
求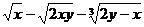 的值.
的值.
19.(6分)已知方程(m-2)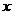 2―2(m―1)
2―2(m―1)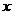 +
+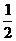 m2=0有一根为l,求m的值,并求这时方程的根。
m2=0有一根为l,求m的值,并求这时方程的根。
20.(7分)如下图,在网格中有一个四边形的图案.
(1)请你画出此图案绕点O顺时针方向旋转90°,180°,270°的图案,你会得到一个美丽的图案,千万不要将阴影位置涂错;
(2)若网格中每个小正方形的边长为1,旋转后点A的对应点依次为A1,A2,A3,求四边形AA1A2A3的面积;
(3)这个美丽图案能够说明一个著名结论的正确性,请直接写出这个结论。
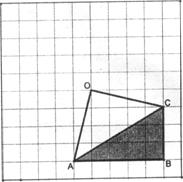
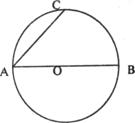
21.(7分)如下图,AB是⊙O的直径,AC是弦,AB=2,AC=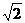 ,请你在图中画出弦AD,使AD=1,你能画出几条呢?画出图形后求∠CAD的度数.
,请你在图中画出弦AD,使AD=1,你能画出几条呢?画出图形后求∠CAD的度数.
22.(7分)如下图,AB是⊙O的直径,BC是弦,OD⊥BC于E,交弧BC于D。若BC=8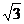 ,∠CBD=30°,求⊙D的半径。
,∠CBD=30°,求⊙D的半径。

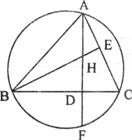
23.(7分)如下图,△ABC的高AD、BE,相交于H,AD的延长线交过△ABC三个顶点的圆于F。求证:DH=FD。
24.(10分)春秋旅行社为吸引市民组团去天水湾风景区旅游,推出了如下收费标准:

某单位组织员工去天水湾风景区旅游,共支付给春秋旅行社旅游费用27000元,请问该单位这次共有多少员工去天水湾风景区旅游?
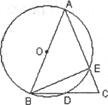
25.(12分)如下图,BC是⊙O的直径,点A在⊙O上,且AB=AC=4,P为AB上一点,过P作PE⊥AB分别交BC、OA于E、F
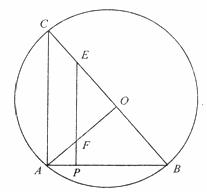
(1)设AP=1,求△EOF的面积;
(2)设AP=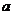 ,(0<
,(0<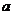 <2),△APF,△OEF的面积分别记为S1,S2;
<2),△APF,△OEF的面积分别记为S1,S2;
①若S1=S2,求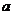 的值;
的值;
②若S=S1+S2,是否存在一个实数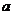 ,使S=
,使S= ,若存在就求出
,若存在就求出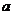 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com