
2008-2009学年度潍坊市昌邑第二学期八年级期中考试
数学试卷
考试时间:90分钟
一、选择题:(每小题3分,共36分.每小题四个选项中,只有一个是正确的。请将正确的选项序号填在右边的括号内.)
1.函数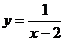 的自变量
的自变量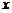 的取值范围是( )
的取值范围是( )
A.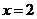 B.
B.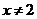 C.
C.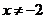 D.
D.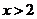
2.下列计算正确的是( )
A.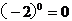 B.
B.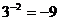
C.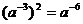 D.
D.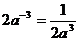
3.小明通常上学时走上坡路,途中速度为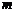 千米/时.放学时沿原路回家走下坡路,途中速度为
千米/时.放学时沿原路回家走下坡路,途中速度为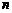 千米/时.则小明上学和放学路上的平均速度为( )
千米/时.则小明上学和放学路上的平均速度为( )
A.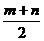 千米/时. B.
千米/时. B.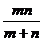 千米/时
千米/时
C.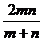 千米/时. D.
千米/时. D.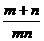 千米/时.
千米/时.
4.已知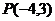 ,与
,与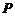 关于
关于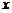 轴对称的点的坐标是( )
轴对称的点的坐标是( )
A.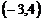 B.
B.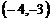 C.
C.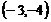 D.
D.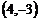
5.若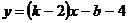 是正比例函数,则( )
是正比例函数,则( )
A.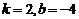 B.
B.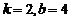 C.
C.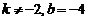 D.
D.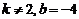
6.关于函数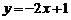 ,下列结论正确的是( )
,下列结论正确的是( )
A.图象必经过点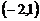 B.图象经过第一、二、三象限
B.图象经过第一、二、三象限
C.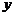 随
随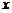 的增大而增大 D.当
的增大而增大 D.当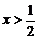 时,
时,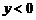
7.甲、乙两同学骑自行车从A地沿同一条路到B地,已知乙比甲先出发,他们离出发地的距离80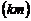 和骑行时间
和骑行时间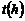 之间的函数关系如图所示,给出下列说法( )
之间的函数关系如图所示,给出下列说法( )
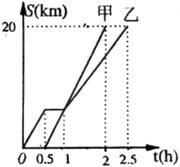
①他们都骑行了20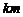 ; ②乙在途中停留了0.5h;
; ②乙在途中停留了0.5h;
③甲、乙两人同时到达目的地; ④相遇后,甲的速度小于乙的速度.
根据图象信息,以上说法正确的有
A.1个 B.2个 C.3个 D.4个
8.如图所示,点B是反比例函数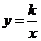 图象上一点,过点B分别作
图象上一点,过点B分别作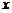 轴、
轴、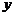 轴的垂线,如果构成的矩形面积是4,那么反比倒函数的解析式是( )
轴的垂线,如果构成的矩形面积是4,那么反比倒函数的解析式是( )
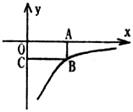
A.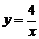 B.
B.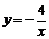 C.
C.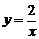 D.
D.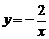
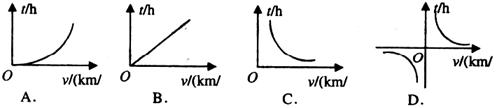
9.已知甲、乙两地相距 ,汽车从甲地匀速行驶到乙地,则汽车行驶的时间
,汽车从甲地匀速行驶到乙地,则汽车行驶的时间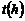 与行驶速度
与行驶速度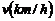 的函数关系图象大致是( )
的函数关系图象大致是( )
10.下列语句中不是命题的是( )
A.延长线段AB B.自然致也是整数
C.两个锐角的和一定是直角 D.同角的余角相等
11.如图,已知△ABC的六个元素,则下面甲、乙、丙三个三角形中和△ABC全等的图形是( )
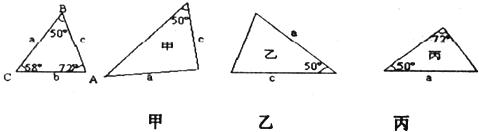
A.甲和乙 B.乙和丙 C.只有乙 D.只有丙
12.下列各组所述几何图形中,一定全等的是( )
A.―个角是45°的两个等腰三角形
B.两个等边三角形
C.腰长相等的两个等腰直角三角形
D.各有―个角是40°,腰长都为5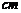 的两个等腰三角形
的两个等腰三角形
二、填空题(每小题3分,共24分)
13.用科学记数法表示:―0.00002005=__________.
14.若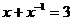 ,则
,则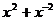 的值是__________.
的值是__________.
15.如果记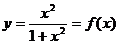 ,并且
,并且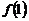 表示当
表示当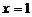 时
时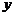 的值,即
的值,即 ;
;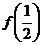 表示当
表示当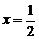 时
时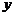 的值,即
的值,即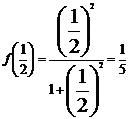 ,…那么
,…那么
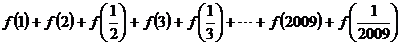 =__________.
=__________.
16.如图,一次函数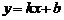 的图象与反比例函数
的图象与反比例函数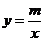 的图象交于A(-2,1),B(1,-2)两点,使一次函数的值大于反比例函数的值的
的图象交于A(-2,1),B(1,-2)两点,使一次函数的值大于反比例函数的值的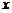 的取值范围__________.
的取值范围__________.
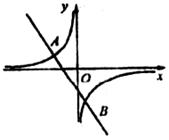
17.把直线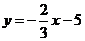 向__________平移__________个单位得到直线
向__________平移__________个单位得到直线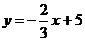 .
.
18.反比例函数 当
当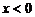 时,
时,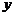 随
随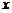 的增大而增大,则
的增大而增大,则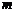 的取值范围是__________.
的取值范围是__________.
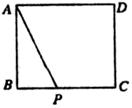
19.已知正方形ABCD的边长为6,如图所示,P为BC边上的一动点,设BP=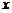 ,试求四边形APCD的面积
,试求四边形APCD的面积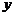 与
与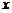
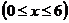 的函数关系式__________.
的函数关系式__________.
20.命题“平行于同一条直线的两条直线平行”的题设为_____________________________,结论为________________________________________.
三、解答题(共60分)
21.(每小题5分)化简与计算:
(1)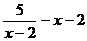
(2)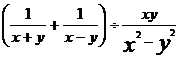
22.(6分)解分式方程: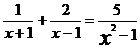
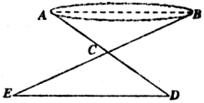
23.(6分)如图,有一池塘,要测量两端A,B的距离,可先在平地上取一个可以直接到达A和B的点C,连接AC并延长到D,使CD=CA.连接BC并延长到E,使CE=CB.连接DE,那么量出DE的长就是A,B的距离。为什么?
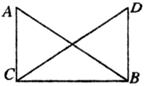
24.(7分)如图,已知AC⊥CB,DB⊥CB,AB=DC.
求证:∠ABD=∠ACD.
25.(8分)列方程解应用题
某校八年级学生由距敬老院10千米的学校出发前往敬老院做义工,一部分同学骑自行车先走,过了20分钟后,其余同学乘汽车出发,结果他们同时到达.已知汽车的速度是骑车同学速度的2倍,求骑车同学的速度.
26.(11分)某移动通讯公司开设两种业务,“全球通”:先缴50元月租费,然后每通话1跳次,再付0.4元;“神州行”:不缴月租费,每通话1跳次,付话费0.6元(本题的通话均指市内通话).若设―个月内通话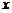 跳次,两种方式的费用分别为
跳次,两种方式的费用分别为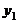 和
和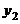 元.(跳次:1min为1跳次。不足1min按1跳次计算,如3.2min为4跳次)
元.(跳次:1min为1跳次。不足1min按1跳次计算,如3.2min为4跳次)
(1)分别写出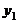 ,
,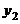 与
与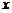 之间的函数关系式;
之间的函数关系式;
(2)一个月内通话多少跳次时,两种方式的费用相同?
(3)某人估计一个月内通话300跳次,应选择哪种合算?
27.(12分)如图,直线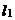 的解析表达式为
的解析表达式为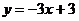 ,且
,且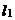 与
与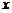 轴交于点D,直线
轴交于点D,直线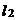 经过点A,B,直线
经过点A,B,直线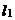 ,
,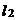 交于点C.
交于点C.
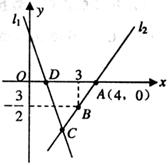
(1)求点D的坐标;
(2)求直线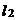 的解析表达式;
的解析表达式;
(3)求△ADC的面积;
(4)在直线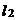 上存在异于点C的另一点P,使得△ADP与△ADC的面积相等,请直接写出点P的坐标.
上存在异于点C的另一点P,使得△ADP与△ADC的面积相等,请直接写出点P的坐标.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com