
2009年福州市初中毕业会考、高级中等学校招生考试
数学试卷(课改实验区)
一、选择题(共10小题,每题4分,满分40分;每小题只有一个正确的选项,请在答题卡的相应位置填涂)
1.2009的相反数是
A.-2009 B.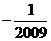 D.
D.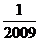
2.用科学记数法表示660 000的结果是
A.66×104 B.6.6×
3.已知∠1=30°,则∠1的余角度数是
A.160° B.150° C.70° D.60°
4.二元一次方程组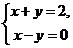 的解是
的解是
A.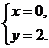 B.
B.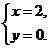 C.
C.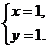 D.
D.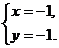
5. 图所示的几何体的主视图是
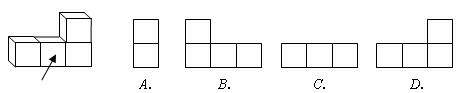
6.下列运算中,正确的是
A.x+x=2x B. 2x-x=
7.若分式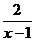 有意义,则x的取值范围是
有意义,则x的取值范围是
A.x≠1 B.x>
8.如图,正五边形FGHMN是由正五边形ABCDE经过位似变换得到的,若AB:FG=2:3,则下列结论正确的是

A.2DE=3MN, B.3DE=2MN, C.3∠A=2∠F D.2∠A=3∠F
9.将1、2、3三个数字随机生成的点的坐标,列成下表。如果每个点出现的可能性相等,那么从中任意取一点,则这个点在函数y=x图象上的概率是
(1,1)
(1,2)
(1,3)
(2,1)
(2,2)
(2,3)
(3,1)
(3,2)
(3,3)
A.0.3 B.0.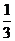 D.
D.
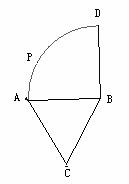
10.如图,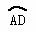 是以等边三角形ABC一边AB为半径的四分之一圆周, P为
是以等边三角形ABC一边AB为半径的四分之一圆周, P为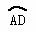 上任意一点,若AC=5,则四边形ACBP周长的最大值是
上任意一点,若AC=5,则四边形ACBP周长的最大值是
A. 15 B.
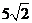 D.15+
D.15+
二、填空题(共5小题,每题4分,满分20分.请将答案填入答题卡的相应位置)
11.分解因式: =
=
12.请写出一个比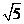 小的整数
小的整数
13. 已知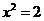 ,则
,则 的值是
的值是
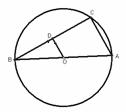
14. 如图,AB是⊙O的直径,点C在⊙O上 ,OD∥AC,若BD=1,则BC的长为
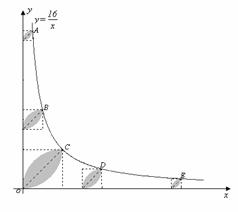
15.已知, A、B、C、D、E是反比例函数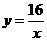 (x>0)图象上五个整数点(横、纵坐标均为整数),分别以这些点向横轴或纵轴作垂线段,由垂线段所在的正方形边长为半径作四分之一圆周的两条弧,组成如图所示的五个橄榄形(阴影部分),则这五个橄榄形的面积总和是 (用含π的代数式表示)
(x>0)图象上五个整数点(横、纵坐标均为整数),分别以这些点向横轴或纵轴作垂线段,由垂线段所在的正方形边长为半径作四分之一圆周的两条弧,组成如图所示的五个橄榄形(阴影部分),则这五个橄榄形的面积总和是 (用含π的代数式表示)
三、解答题(满分90分.请将答案填入答题卡的相应位置)
16.(每小题7分,共14分)
(1)计算:22-5×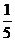 +
+
(2)化简:(x-y)(x+y)+(x-y)+(x+y)
17.(每小题8分,共16分)
(1)解不等式: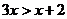 ,并在数轴上表示解集.
,并在数轴上表示解集.
(2)整理一批图书,如果由一个人单独做要花60小时。现先由一部分人用一小时整理,随后增加15人和他们一起又做了两小时,恰好完成整理工作。假设每个人的工作效率相同,那么先安排整理的人员有多少人?
18.(满分10分)
如图,已知AC平分∠BAD,∠1=∠2,求证:AB=AD

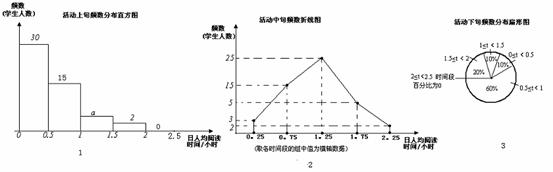
(1)从以上统计图可知,九年级(1)班共有学生 人;
(2)图1中a的值是 ;
20.(满分12分)
如图,在边长为1的小正方形组成的网格中,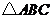 的三个顶点均在格点上,
的三个顶点均在格点上,
请按要求完成下列各题:
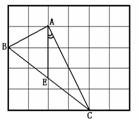
(1)用签字笔画AD∥BC(D为格点),连接CD;
(2)线段CD的长为 ;
(3)请你在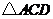 的三个内角中任选一个锐角,若你所选的锐角是 ,则它所对应的正弦函数值是
。
的三个内角中任选一个锐角,若你所选的锐角是 ,则它所对应的正弦函数值是
。
(4)若E为BC中点,则tan∠CAE的值是
21.(满分12分)
如图,等边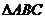 边长为4,
边长为4,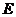 是边
是边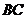 上动点,
上动点, 于H,过
于H,过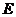 作
作 ∥
∥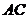 ,交线段
,交线段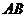 于点
于点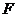 ,在线段
,在线段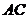 上取点
上取点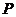 ,使
,使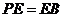 。设
。设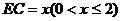 。
。

(1)请直接写出图中与线段 相等的两条线段(不再另外添加辅助线);
相等的两条线段(不再另外添加辅助线);
(2)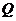 是线段
是线段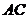 上的动点,当四边形
上的动点,当四边形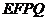 是平行四边形时,求 四边形EFPQ的面积(用含
是平行四边形时,求 四边形EFPQ的面积(用含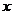 的代数式表示);
的代数式表示);
(3)当(2)中 的四边形EFPQ面积最大值时,以E为圆心,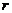 为半径作圆,根据⊙E与此时
为半径作圆,根据⊙E与此时 四条边交点的总个数,求相应的
四条边交点的总个数,求相应的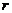 的取值范围。
的取值范围。
22.(满分14分)
已知直线l:y=-x+m(m≠0)交x轴、y轴于A、B两点,点C、M分别在线段OA、AB上,且OC=2CA,AM=2MB,连接MC,将△ACM绕点M旋转180°,得到△FEM,则点E在y轴上, 点F在直线l上;取线段EO中点N,将ACM沿MN所在直线翻折,得到△PMG,其中P与A为对称点.记:过点F的双曲线为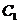 ,过点M且以B为顶点的抛物线为
,过点M且以B为顶点的抛物线为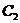 ,过点P且以M为顶点的抛物线为
,过点P且以M为顶点的抛物线为 .
.
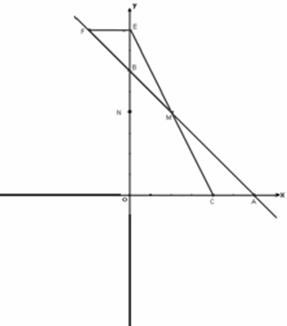
(1)如图,当m=6时,
①直接写出点M、F的坐标,
②求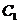 、
、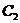 的函数解析式;
的函数解析式;
(2)当m发生变化时,
①在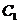 的每一支上,y随x的增大如何变化?请说明理由。
的每一支上,y随x的增大如何变化?请说明理由。
②若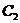 、
、 中的y都随着x的增大而减小,写出x的取值范围。
中的y都随着x的增大而减小,写出x的取值范围。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com