
2010届重庆一中第一学期九年级10月月考
数学试卷
一.选择题:(本题共10个小题,每个小题4分,共40分)
1.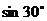 的值为( )
的值为( )
A.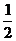 B.
B.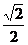 C.
C.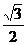 D.
D.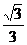
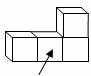
2.如图所示的几何体的主视图是( )
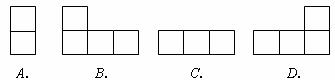
3.如果分式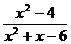 的值为0,则
的值为0,则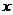 的值为( )
的值为( )
A.-2
B.
4.关于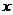 的一元二次方程
的一元二次方程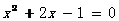 的根的情况是( )
的根的情况是( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.没有实数根 D.不能确定
5.抛物线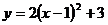 可由抛物线
可由抛物线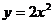 经过下列平移得到( )
经过下列平移得到( )
A.向左平移1个单位,向上平移3个单位
B.向右平移1个单位,向上平移3个单位
C.向右平移3个单位,向上平移1个单位
D.向左平移3个单位,向下平移1个单位
6.在一次爱心捐款活动中,某小组7名同学捐款数额分别是(单位:元)50,20,50,30,50,25,95,这组数据的众数和中位数分别是( )
A.50,20 B.50,
7.如图,小王同学从A地沿北偏西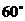 方向走
方向走
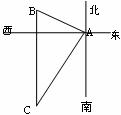
A.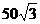 米 B.
米 B.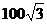 米
米
8.已知二次函数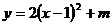 的图象上有三个点,坐标分别为
的图象上有三个点,坐标分别为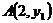 、
、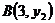 、
、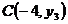 ,则
,则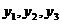 的大小关系是( )
的大小关系是( )
A.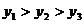 B.
B.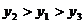
C.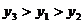 D.
D.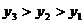
9.如图,已知菱形ABCD的边长为2┩,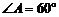 ,点M从点A出发,以1┩/s的速度向点B运动,点N从点A 同时出发,以2┩/s的速度经过点D向点C运动,当其中一个动点到达端点时,另一个动点也随之停止运动。则△AMN的面积
,点M从点A出发,以1┩/s的速度向点B运动,点N从点A 同时出发,以2┩/s的速度经过点D向点C运动,当其中一个动点到达端点时,另一个动点也随之停止运动。则△AMN的面积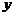 (┩2)与点M运动的时间
(┩2)与点M运动的时间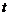 (s)的函数的图像大致是( )
(s)的函数的图像大致是( )
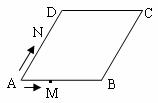
10.如图,△ABC为等腰直角三角形,∠BAC=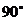 ,BC=2, E为AB上任意一动点,以CE为斜边作等腰Rt△CDE,连结AD,下列说法:①∠BCE=∠ACD;②AC⊥ED;③△AED∽△ECB;④AD∥BC;⑤四边形ABCD的面积有最大值,且最大值为
,BC=2, E为AB上任意一动点,以CE为斜边作等腰Rt△CDE,连结AD,下列说法:①∠BCE=∠ACD;②AC⊥ED;③△AED∽△ECB;④AD∥BC;⑤四边形ABCD的面积有最大值,且最大值为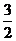 。其中,正确的结论是( )
。其中,正确的结论是( )
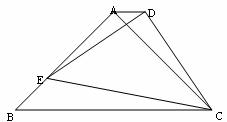
A.①②④ B.①③⑤ C.②③④ D.①④⑤
二.填空题:(本题共6个小题,每小题4分,共24分)
11.一元二次方程: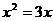 的解是:
;
的解是:
;
12.某人沿坡度为1: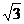 的斜坡前进了
的斜坡前进了
13.用配方法将二次函数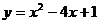 化为
化为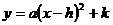 的形式为
的形式为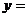 ;
;
14.飞机着陆后滑行的距离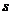 (单位:米)与滑行的时间
(单位:米)与滑行的时间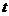 (单位:秒)之间的函数关系式是
(单位:秒)之间的函数关系式是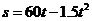 ,飞机着陆后滑行 秒才能停下来;
,飞机着陆后滑行 秒才能停下来;
15.现有A、B两枚均匀的小立方体(立方体的每个面上分别标有数字1、2、3、4、5、6)用小明掷A立方体朝上的数字为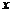 ,小明掷B立方体朝上的数字为
,小明掷B立方体朝上的数字为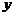 来确定点P(
来确定点P(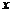 ,
,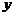 ).则小明各掷一次所确定的点P落在已知抛物线
).则小明各掷一次所确定的点P落在已知抛物线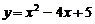 上的概率是
上的概率是
16.已知二次函数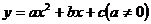 的图象如图所示,
的图象如图所示,
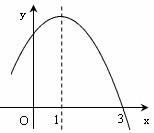
则下列5个结论:①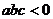 ; ②
; ②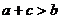 ;③
;③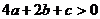 ④
④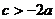 ;
;
⑤ 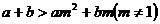 .
.
其中正确的结论有 (填序号)
三.解答题:(本题共4题,每小题6分,共24分)
17.计算: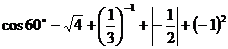
18.解方程: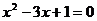
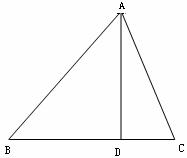
19.已知:如图,在△ABC中,AD是边BC上的高,
BC=14,AD=12,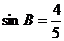 ,求:(1)线段BD的长;(2)
,求:(1)线段BD的长;(2)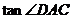 的值.
的值.
20.先化简,再求值: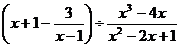 ,其中
,其中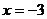 ;
;
四. 解答题:(本题共4题,每小题10分,共40分)
21.某水果批发商经销一种高档水果,如果每千克赢利10元,每天可售出500千克.经市场调查发现,在进货价不变的情况下,若每千克涨价1元,日销售量将减少20千克.现该商场要保证每天赢利6000元,同时又要使顾客得到实惠,那么每千克应涨价多少元?

22.已知:二次函数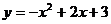
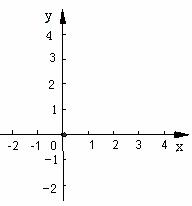
(1)求函数图象的顶点P的坐标;
(2)设函数图象与y轴交于点C,与x轴交于点A、B(点A在点B的左侧),求点A、B、C的坐标;
(3)根据对称轴、点P、A、B、C的坐标,在如图所示的坐标系内,画出二次函数的示意图,并求出△PBC的面积.
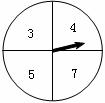
23.有一个可以自由转动的转盘,被分成了4个相同的扇形,分别标有数3、4、5、7(如图所示),另有一个不透明的口袋装有分别标有数0、1、3的三个小球(除数不同外,其余都相同)。小李转动一次转盘,停止后指针指向某一扇形(如果指针恰好指在分割线上,那么重转一次),用扇形内的数作为被减数,小张任意摸出一个小球,用小球上的数作为减数,然后计算这两个数的差。
(1)请你用画树状图或列表的方法,求这两个数的差为4的概率;
(2)小李与小张做游戏,规则是:若这两个数的差为奇数,小李赢;否则,小张赢。你认为该游戏公平吗?为什么?如果不公平,请你修改该游戏规则,使游戏公平。
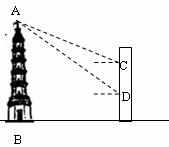
24.如图,已知大楼的每层高为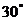 ,他为了测量此塔的高度,于是下到住在同一单元第9层的同学小亮家的阳台D处又测得塔顶A的仰角为
,他为了测量此塔的高度,于是下到住在同一单元第9层的同学小亮家的阳台D处又测得塔顶A的仰角为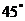 ,请你帮他算算这座塔有多高?(小明的身高忽略不计,塔底与楼底在同一水平面上)(结果精确到
,请你帮他算算这座塔有多高?(小明的身高忽略不计,塔底与楼底在同一水平面上)(结果精确到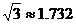 )
)
五. 解答题:(本题共2题,第25题10分,第26题12分,共22分)
25.某市种植某种绿色蔬菜,全部用来出口.为了扩大出口规模,该市决定对这种蔬菜的种植实行政府补贴,规定每种植一亩这种蔬菜一次性补贴菜农若干元.经调查,种植亩数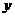 (亩)与补贴数额
(亩)与补贴数额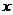 (元)之间大致满足如图1所示的一次函数关系,但种植面积不超过3200亩.随着补贴数额
(元)之间大致满足如图1所示的一次函数关系,但种植面积不超过3200亩.随着补贴数额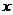 的不断增大,出口量也不断增加,但每亩蔬菜的收益
的不断增大,出口量也不断增加,但每亩蔬菜的收益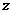 (元)会相应降低,且
(元)会相应降低,且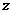 与
与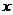 之间也大致满足如图2所示的一次函数关系,且每亩收益不低于1800元.
之间也大致满足如图2所示的一次函数关系,且每亩收益不低于1800元.

(1)分别求出政府补贴政策实施后,种植亩数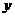 和每亩蔬菜的收益
和每亩蔬菜的收益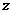 与政府补贴数额
与政府补贴数额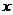 之间的函数关系式;
之间的函数关系式;
(2)在政府未出台补贴措施前,该市种植这种蔬菜的总收益额为多少?
(3)要使全市这种蔬菜的总收益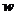 (元)最大,政府应将每亩补贴数额
(元)最大,政府应将每亩补贴数额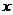 定为多少?并求出总收益
定为多少?并求出总收益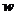 的最大值.
的最大值.
26.已知:二次函数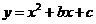 的图象与x轴交于A,B两点,其中A点坐标为(-3,0),与y轴交于点C,点D(-2,-3)在抛物线上.
的图象与x轴交于A,B两点,其中A点坐标为(-3,0),与y轴交于点C,点D(-2,-3)在抛物线上.
(1)求抛物线的解析式;
(2)抛物线的对称轴上有一动点P,求出PA+PD的最小值;
(3)点G抛物线上的动点,在x轴上是否存在点E,使B、D、E、G这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的E点坐标;如果不存在,请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com