
2008-2009学年度聊城市冠县第一学期九年级期末学业水平评价
数学试卷
第Ⅰ卷(选择题 共36分)
一.选择题(本大题共12个小题,共36分,在每小题给出的四个选项中,只有一个选项符合题意)
1.在Rt△ABC中,∠C=90°,cosA=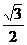 ,则∠A的度数是( )
,则∠A的度数是( )
A.30° B.45° C.60° D.90°
B.45° C.60° D.90°
2.抛物线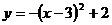 的对称轴是( )
的对称轴是( )
A.直线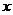 =-3 B.直线
=-3 B.直线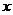 =
=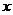 =-2 D.直线
=-2 D.直线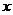 =2
=2
3.如图,在△ABC中,D、E、F分别是AB、AC、BC的中点,则△DEF与△ABC的周长之比为( )

A.1: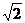 B.1:2 C.1:3 D.1:4
B.1:2 C.1:3 D.1:4
4.如图,将△AOB绕点O逆时针方向旋转90°,得到△A’OB’,若点A的坐标为(2,1),则点A ’坐标为( )
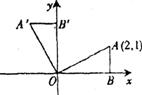
A.(-1,-2) B.(-1,2) C.(-2,1) D.(-2,-1)
5.如果非零实数a、b、c满足a - b + c=0,则关于x的一元二次方程 必有一根为( )
必有一根为( )
A.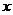 =1 B.
=1 B.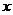 =-1 C.
=-1 C.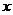 =0 D.
=0 D.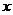 =2
=2
6.在元旦游园晚会上有一个闯关活动:将5张分别画有圆、等腰梯形、平行四边形、等腰三角形、菱形的卡片任意摆放,将所有图形的正面朝下,从中任意翻开一张,如果翻开的图形是轴对称图形就可以过关,那么一次过关的概率是( )
A.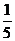 B.
B. C.
C.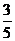 D.
D.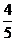
7.如图,在梯形ABCD中,AB∥CD,E是AD的中点,EF∥CB交AB于F,BC=4cm,则EF的长为( )

A.2cm B.2.5cm C.3cm D.3.5cm
8.抛掷一枚硬币三次,三次朝上的面均相同的概率为( )
A.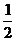 B.
B.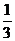 C.
C.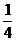 D.
D.
9.如图,在梯形ABCD中,AD∥BC,AD=2,AB=3,BC=6,沿AE翻折梯形ABCD使点B落AD的延长线上,记为点B’,连结B’E交CD于点F,则 的值为( )
的值为( )
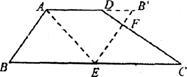
A.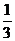 B.
B.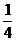 C.
C.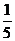 D.
D.
10.如图,在平面直角坐标系中,二次函数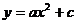 (a≠0)的图象过边长为1的正方形ABOC的三个顶点A、B、C,则a c的值为( )
(a≠0)的图象过边长为1的正方形ABOC的三个顶点A、B、C,则a c的值为( )
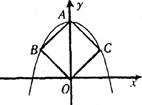
A.-2 B.-1 C.-
B.-1 C.-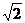 D.
D.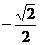
11.如图所示,已知△ABC的周长为1,连接△ABC三边的中点构成第二个三角形,再连接第二个三角形三边中点构成第三个三角形,依次类推,第2008个三角形的周长为( )
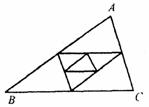
A. B.
B. C.
C. D.
D.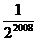
12.已知二次函数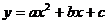 的图象如图所示,对称轴是
的图象如图所示,对称轴是 ,则在“①b<0,②ac<0,③4a+c>2b,④a+c>b”中判断正确的个数是( )
,则在“①b<0,②ac<0,③4a+c>2b,④a+c>b”中判断正确的个数是( )

A.1个 B.2个 C.3个 D.4个
第Ⅱ卷(非选择题 共84分)
二、填空题(本题共5小题,每小题3分,满分15分,只要求填写最后的结果)
13.计算: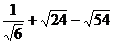 = ___________.
= ___________.
14.已知抛物线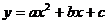 与
与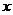 轴交点的横坐标为-1,则a + c=___________.
轴交点的横坐标为-1,则a + c=___________.
15.在一个不透明的盒子中装有2个白球,n个黄球,它们除颜色不同外,其余均相同.若从中随机摸出一个球,它是白球的概率为 ,则n=___________
,则n=___________
16.如图,在△ABC中,DE∥BC,若AD/DB= 1/3,已知DE=3cm;则BC=___________cm.

17.如图,在梯形ABCD中,AD∥BC,AB=DC=AD=6,点E、F分别在线段AD、DC上运动(点E与点A、D不重合),若∠ABC=60°,∠BEF=120°,AE= x,DF= y,则y关于x的函数关系式为___________.
三、解答题(本题共8小题,共69分.解答应写出必要的文字说明、推理过程或演算步骤)
18.(本题满分6分)计算:
(1)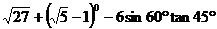
(2)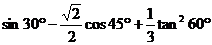
19.(本题满分6分)按指定的方法解方程:
(1)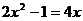 (用配方法);
(用配方法);
(2) (因式分解法).
(因式分解法).
20.(本题满分6分)
如图,河旁有一座小山,从山顶A处测得河对岸点C的俯角为30°,测得岸边点D的俯角为45°,又知河宽CD为20米。现需从山顶A到河对岸点C拉一条笔直的缆绳AC,求缆绳AC的长.(答案保留根号)

21.(本题满分8分)
某工程队在我市旧城改造过程中承包了一项拆迁工程,原计划每天拆迁1250m2,因为准备工作不足,第一天少拆迁了20%,从第二天开始,该工程队加快了拆迁速度,第三天拆迁了1440m2.
(1)求该工程队第一天拆迁的面积;
(2)若该工程队第二天、第三天每天的拆迁面积比前一天增加的百分数相同,求这个百分数.
22.(本题满分10分)、
甲、乙两大型超市为了吸引顾客,都举行有奖酬宾活动,凡购物满100元,均可得到一次摸奖的机会,在一个纸盒里装有2个红球和2个白球,除颜色外其它都相同,摸奖者一次从中摸出两个球,根据球的颜色决定送礼金券(在他们超市使用时,与人民币等值)的多少(如下表).
甲超市.
球
两红
一红一白
两白
礼金券(元)
5
10
5
乙超市:
球
两红
一红一白
两白
礼金券(元)
10
5
10
(1)用树状图表示得到一次摸奖机会时中礼金券的所有情况;
(2)如果只考虑中奖因素,你将会选择去哪个超市购物?请说明理由.
23.(本题满分10分)
如图,平面直角坐标系中有一个边长为2的正方形AOBC,M为OB的中点,将△AOM沿直线AM对折,使O点落在O’处,连结OO’,过O’点作O’N⊥OB于N.
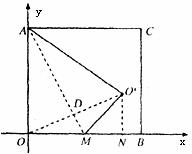
(1)写出点A、C的坐标;
(2)判断△AOM与△ONO’是否相似,若是,请给出证明.
24.(本题满分12分)
某公司经销一种商品,每件商品的成本为50元,经市场的调查,在一段时间内,销售量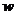 (件)随销售单价
(件)随销售单价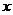 (元/件)的变化而变化,具体关系式为
(元/件)的变化而变化,具体关系式为 +240,
+240,
设这种商品在这段时间内的销售利润为 (元),解答如下问题:
(元),解答如下问题:
(1)求 与
与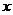 的关系式;
的关系式;
(2)当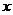 取何值时,
取何值时, 的值最大?
的值最大?
(3)如果物价部门规定这种商品的销售单价不得高于80元/件,公司想要在这段时间内获得2250元的销售利润,销售单价应定为多少元?
25.(本题满分13分)
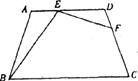
如图,等腰梯形ABCD中,AD∥BC,AD=3,BC=7,∠B=60°,P为下底BC上一点(不与B、C重合),过P点作PE交DC于F,使得∠APE=∠B.
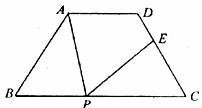
(1)求等腰梯形的腰长;
(2)证明:△ABP∽△PCE;
(3)在底边BC上是否存在一点P,使得DE:EC=5:3?如果存在,求出BP的长;如果不存在,请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com