
东北三省四市长春、哈尔滨、沈阳、大连
2009年高中毕业班第二次调研测试
数学试题(文)
本试卷分为第I卷(选择题)和第Ⅱ卷(非选择题)两部分,共4页,试卷满分150分,做题时间为120分钟.考试结束后,将试卷和答题卡一并交回.
注意事项:
1.答题前,考生必须将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形
码区域内.
2.选择题必须用2B铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,
字体工整、笔迹清楚.
3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草
稿纸、试题卷上答题无效.
4.保持卡面清洁,不要折叠、不要弄破、不准使用涂改液、刮纸刀.
第I卷(选择题,共60分)
一、选择题(本大题共12小题,每小题5分。共60分,在每小题的四个选项中。只有一项
1.已知集合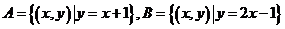 ,则
,则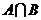 = ( )
= ( )
A.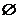 B.
B.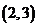 C.
C.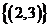 D.
D.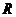
2.在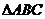 中,
中,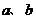 分别是角A、B所对的边,条件“
分别是角A、B所对的边,条件“ ”是使“
”是使“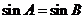 ”成
”成
立的 ( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
3.已知数列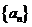 ,满足
,满足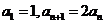 ,则
,则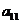 = ( )
= ( )
A.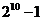 B.
B.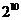 C.
C.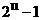 D.
D.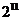
4.已知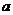 、
、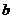 为两条直线,
为两条直线,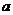 、
、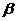 为两个平面,下列四个命题
为两个平面,下列四个命题
①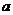 ∥
∥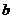 ,
,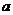 ∥
∥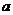
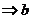 ∥
∥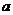 ; ②
; ②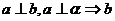 ∥
∥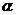 ;
;
③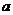 ∥
∥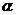 ,
,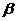 ∥
∥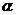
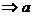 ∥
∥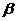 ; ④
; ④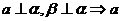 ∥
∥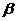 ,
,
其中不正确的有 ( )
A.1个 B.2个 C.3个 D.4个
5.在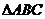 中,
中,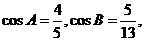 则
则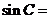 ( )
( )
A.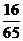 B.
B.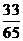 C.
C.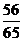 D.
D.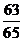
6. 过点P(2,3)向圆上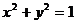 作两条切线PA、PB,则弦AB所在直线方程为( )
作两条切线PA、PB,则弦AB所在直线方程为( )
A.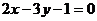 B.
B.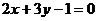
C.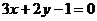 D.
D.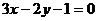
7.将函数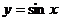 的图象经过下列哪种变换可以得到函数
的图象经过下列哪种变换可以得到函数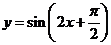 的图象( )
的图象( )
A.先向左平移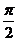 个单位,然后再沿
个单位,然后再沿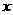 轴将横坐标压缩到原来的
轴将横坐标压缩到原来的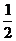 倍(纵坐标不变)
倍(纵坐标不变)
B.先向左平移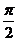 个单位,然后再沿
个单位,然后再沿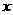 轴将横坐标伸长到原来的2倍(纵坐标不变)
轴将横坐标伸长到原来的2倍(纵坐标不变)
C.先向左平移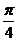 个单位,然后再沿
个单位,然后再沿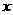 轴将横坐标压缩到原来的
轴将横坐标压缩到原来的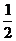 倍(纵坐标不变)
倍(纵坐标不变)
D.先向左平移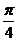 个单位,然后再沿
个单位,然后再沿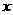 轴将横坐标伸长到原来的2倍(纵坐标不变)
轴将横坐标伸长到原来的2倍(纵坐标不变)
8.已知实数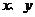 满足
满足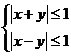 ,则
,则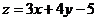 的最大值为 ( )
的最大值为 ( )
A.-9 B.
9.四张卡片上分别标有数字“
卡片可组成不同的四位数的个数为 ( )
A.6 B.
10.若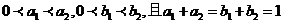 ,则下列各数中最大的是 ( )
,则下列各数中最大的是 ( )
A.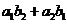 B.
B.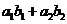 C.
C.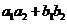 D.
D.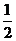
11.定长为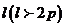 的线段AB的两端点都在抛物线
的线段AB的两端点都在抛物线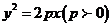 上,则AB中点M
上,则AB中点M
的横坐标的最小值为 ( )
A.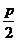 B.
B.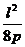 C.
C.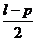 D.
D.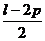
12. 已知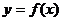 是
是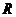 上的可导函数,对于任意的正实数
上的可导函数,对于任意的正实数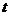 ,都有函数
,都有函数
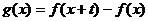 在其定义域内为减函数,则函数
在其定义域内为减函数,则函数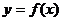
的图象可能为下图中的 ( )
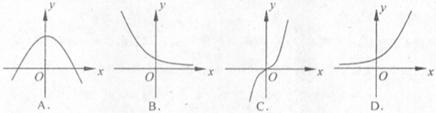 |
|||||
| |||||