练习册

  • 练习册
  • 试题

    山东省实验中学2010届高一阶段性评估试题

    数学试题

    注意事项：

    1．本试题分为第Ⅰ卷和第Ⅱ卷两部分，满分150分，考试时间为120分钟。

    2．答第Ⅰ卷前务必将自己的姓名．考号．考试科目涂写在答题卡上。考试结束，试题和答题卡一并收回。

    3．第Ⅰ卷每题选出答案后，都必须用2B铅笔把答题卡上对应题目的答案标号（ABCD）涂黑，如需改动，必须先用橡皮擦干净，再改涂其它答案。

     

    第Ⅰ卷

     

    一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的，请把正确答案的代号填在题后的括号内（本大题共12个小题，每小题5分，共60分）。

    1．下面算法描述正确的一项是                                             （　　）

       A．算法只能用自然语言来描述        

       B．算法只能用程序语言来表示

       C．同一问题的算法不同，结果必然不同

       D．同一问题可以有不同的算法

    试题详情

    2．下列语句中，哪一个是输入语句                                         （　　）

       A．PRINT           B．IF            C．INPUT           D．WHILE

    试题详情

    3．下列图形中，是条件语句的一般格式的是                                 （　　）

    试题详情

     

     

     

     

     

     

     

     

     

    试题详情

    4． 小芳妈妈出差了，爸爸中午要在公司加班，中午放学回家只能自己煮面条吃，有下面几道工序需完成：①洗锅盛水3分钟；②洗菜7分钟；③准备面条及佐料3分钟；④用锅把水烧开10分钟；⑤煮面条和菜共3分钟。以上各道工序，除了④之外，一次只能进行一道工序。小芳要将面条煮好，最少要用(      )分钟。                                    （　　）

       A．16              B．15            C．14              D．13

    试题详情

    5．数1037和425的最大公约数是                                          （    ）

       A．51              B．17            C．9               D．3

    试题详情

    6．下面左图为一个求高一（1）班46个同学的数学平均分的程序,在横线上应填充的语句为    

                                                                            （　　）           

       A．i>=46           B．i<46          C．i>46            D．i<=46

    试题详情

    S=0

    i=1

    DO

     INPUT  x

     S=S+x

     i=i+1

    LOOP UNTIL  _____

    a=S/46

    PRINT  a

    END

    (第6题)

     

     

     

     

     

    试题详情

    文本框: n=5 S=0 WHILE S<10 S=S+n n=n－1 WEND PRINT n END (第7题)

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

    试题详情

    7．上面中图程序执行后输出的结果是                                       （　　）

    A．2             B．1             C．0               D．－1

    试题详情

    8．如右图所示的程序框图中，如果输入三个实数为a＝3，b＝7，c＝２，则输出结果为（　　）

    A．2              B．3             C．7               D．x

    试题详情

    9．用秦九韶算法计算多项式,当时的值时,需要做乘法和加法的次数分别是                                                            （　　）

       A． 6 , 5          B．5 , 6         C．5 , 5           D．6 , 6

    试题详情

    10．某流程如右图所示，现输入如下四个函数，则可以输出的函数是            （    ）

    试题详情

    A．                       

    试题详情

    B．

    试题详情

    C．                      

    试题详情

    D．

    试题详情

    11．给出以下四个问题：

    试题详情

    ①解不等式＞（且）.

    试题详情

    ②求边长为的正三角形的面积.

    试题详情

    ③求函数的函数值.

    试题详情

      ④若集合，，

    试题详情

    文本框: INPUT m , n DO r=m MOD n m=n n=r LOOP UNTIL r=0 PRINT m END （第12题） 且，求的值。

      其中不需要用条件语句来描述其算法的有（　　）

    试题详情

       A．个             B．个         

    试题详情

       C． 个           D． 个

    试题详情

    12．运行如右程序： 当输入168，72时，输出

    的结果是                           （　　）                                              

       A．12　　　　      B．24　

       C．36　　          D．72

     

    第Ⅱ卷

    试题详情

    二、填空题：请把答案填在题中横线上（本大题共4个小题，每小题4分，共16分）。

    13．函数f(x)＝  ，求f{f[f(3)]}的算法时，下列步骤正确的顺序是           。

    (1)由3＞0，得f(3)＝0

    (2)由－5＜0，得f(－5)＝25＋2＝27,即f{f[f(3)]}＝27

    (3)由f(0)＝－5,得f[f(3)]＝f(0)＝－5

     

    x＝5

    y＝－12

    IF  x<0  Then

       x＝y－3

    Else

       x＝y+3

    End If

    Print  x－y

    End    （第14题）

    试题详情

    15．下列各数．．．中

    最小的数是___________。

    试题详情

    16．在下面的程序框图中，如果运行的结果为S＝120，

    那么判断框中应填入            

    试题详情

     

    试题详情

    三、解答题：解答应写出文字说明．证明过程或演算步骤(本大题共6个大题，共74分).

    17．已知圆锥的底面半径为，母线长为，设计一个求该圆锥体积的算法．

     

     

     

     

     

     

     

    试题详情

    18．高等数学中经常用到符号函数，符号函数的定义为，试写出算法，并画出程序框图实现输入x的值，输出y的值．

     

     

     

     

     

     

     

     

     

    试题详情

    19．下面是利用UNTIL循环设计的计算的一个算法程序．

    S＝1

    I=1

    DO

          ①   

      I=I+2

    LOOP  UNTIL      ②    

    PRINT S

    END

    （Ⅰ）请将其补充完整，并转化为WHILE循环；

      （Ⅱ）绘制出该算法的流程图．

    解：（Ⅰ）补充如下：               （Ⅱ）流程图绘制如下：（请画在下框中）

     

     

       

    ②                        ．

     

    WHILE循环为

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

    试题详情

    20．2008年3月1日开始实施的《个人所得税法》规定：全月总收入不超过元的免征个人工资．薪金所得税，超过元部分需征税．设全月总收入金额为元，前三级税率如右表所示：当工资薪金所得不超过元，写出计算个人所得税的一个算法程序。

    级数

    试题详情

    全月应纳税金额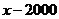

    税率

    1

    试题详情

    不超过元的部分

    5%

    2

    试题详情

    超过至的元部分

    10%

    3

    试题详情

    超过至的元部分

    15%

    ……

    ……

    ……

     

     

     

     

     

     

     

    试题详情

    21．在2008年北京奥运会上，林跃．火亮为观众上演了一场精彩的表演，最终以468.18的高分毫无悬念的夺得男子10米比双人跳台的冠军，这次比赛共有7名裁判打分，在第二轮跳水中，林跃．火亮的难度系数为2.0，7名评委给他们评定的成绩分别是：10，9.5，10，10，9.5，10，10，程序框图用来编写程序统计每位选手的成绩，试根据下面所给条件回答下列问题：

       （1）在程序框图中，用k表示评委人数，用

    a表示选手的成绩（各评委所给有效分

    的平均值乘以3，再乘以难度系数）。横

    线①②处应填什么？“s1=s-max-min”

    的含义是什么？

       （2）根据程序框图，计算林跃．火亮在第二

    轮跳水的成绩是多少？

     

     

     

     

     

     

     

     

     

     

    试题详情

    22．某汽车城销售某种型号的汽车，每辆进货价为25万元，市场调研表明：当销售价为流程图的输出结果万元时，平均每周能售出8辆，而当销售价每降低0.5万元时，平均每周能多售出4辆．如果设每辆汽车降价万元，每辆汽车的销售利润为万元．（销售利润销售价进货价）

    试题详情

       （1）求与的函数关系式；在保证商家不亏本的前提下，写出的取值范围；

    试题详情

       （2）假设这种汽车平均每周的销售利润为万元，试写出与之间的函数关系式；

       （3）当每辆汽车的定价为多少万元时，平均每周的销售利润最大？最大利润是多少？

    试题详情

     

     

     

     

    试题详情

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

    试题详情

     

    一、选择题

    1．D．　

    解：算法可用自然语言．图形符号或程序语言描述，故A．．B．错。不同的算法，结果相同，故C．也错。

    2．C．　

    解：A．是输出语句，B．是条件语句，D．是循环语句。

    3．C．　

    解：条件结构是先判断，判断是菱形框，然后执行语句。

    4．B．　

    解：第一步：①洗锅盛水3分钟; 第二步：④用锅把水烧开10分钟（同时进行以下两步：②洗菜7分钟;③准备面条及佐料3分钟;）;第三步：⑤煮面条和菜共3分钟共需16分钟。

    5．B．　

    解：1037＝425×2＋187，425＝187×2＋51，187＝51×3+34，51＝34×1+17，34＝17×2

    6．C．　

    解：这是一个直到型循环，当i=46时，输入第46个学生成绩，当i>46时退出循环。

    7．A．　

    解：第一步：S=5，n=4；第二步：S=9，n=3；第三步：S=12，n=2。

    ８．C．　

    解：这是一个输出三个数中最大数的程序算法。

    9．(D)　　

    解：，6次乘法，6次加法。

    10．D．　

    解：由程序框图可知，f（x）必须是奇函数，可排除A．．C．，且f（x）=0有解，排除B．，事实上，对于D．，f(-x)=，当x=0时，f（x）=0。

    11．A． 

    解：仅②不需要分情况讨论，即不需要用条件语句

    12．B．　

    解：当m≥n>0时，该程序的作用是求两个正整数的最大公约数，

        因为168与72的最大公约数是24，所以输出结果是24．

    二、填空题

    13．（1）（3）（2）

    14．3

    解：因为x＝5＞0，所以，x＝－12＋3＝－9，所以，x－y＝－9＋12＝3

    15．

    解： ，   ，

     ．

    16．k≤3？

    解：第一次循环时S＝1×6＝6,，k＝6－1＝5；

    第二次循环时，S＝6×5=30，k=5－1＝4；

    第三次循环时，S＝30×4=120，k=4－1＝3；

    此时S=120是题目中程序运行的结果，因此，循环必须终止；所以判断框中应填入的为“k≤3？”。

    三、解答题

    17．解：

    第一步：由勾股定理，可求出圆锥的高＝；

    第二步：计算圆锥底面积：Ｓ＝２；

    第三步：计算圆锥的的体积：Ｖ＝

    第四步：输出体积。

    18．解：第一步：输入x的值；

    第二步：判断x的值，如果x>0，则y=1，否则，如果x=0，则y=0，否则y=-1。

    第三步：输出y的值。

    程序框图如下：

    19．解：（Ⅰ）补充如下：

    ① S=S*I

    ②I>99

    WHILE循环程序如下：

    S=1

    I=1

    WHILEI<=99

    S=SI

    I=I+2

    WEND

    PRINT S

    END

    （Ⅱ）流程图如右图

    20．解：设个人所得税为y元，则依题意，得：

    y＝

    程序如下：

    输入x

    IF　x≤2000  THEN

    　  y＝0

    ELSE

    IF　x≤2500 THEN

    　　 y＝0.05（x－2000）

       ELSE

    　y＝0.1（x－2000）－25

    END IF

    END IF

    PRINT  y

    21．解：(Ⅰ)  ① k≤7  ，       

    ②a=（s1/5）*3*2 ，

    “s1=s-max-min”的含义是：在计算每位选手的平均分数时，为了避免个别评委所给的极端分数的影响，必须去掉一个最高分和一个最低分，再求应得分。

    (2)去掉一个10分，一个9.5分，剩下五个评委的分数之和为：49.5，故×3×2＝59.4

    所以，林跃．火亮在第二轮跳水的成绩是59.4分。

    22．解：（1）由流程图，可得：p＝29，

    所以，，　　即

    （2）

    所以z与x之间的函数关系式为：

    （3）

    当时，

    当定价为万元时，有最大利润，最大利润为50万元．

    　  或：当

     

    当定价为万元时，有最大利润，最大利润为50万

     

     


    同步练习册答案