YCY
1、分别在区间[1,6]和[2,4]内任取一实数,依次记为m和n,则 的概率为
的概率为
2、一个社会调查机构就某地居民的月收入调查了10 000人,并根据所得数据画了样本的频率分布直方图(如下图).为了分析居民的收入与年龄、学历、职业等方面的关系,要从这10 000人中再用分层抽样方法抽出100人作进一步调查,则在[2500,3000)(元)月收入段应抽出
人.

3、已知 、
、 是三个互不重合的平面,
是三个互不重合的平面, 是一条直线,给出下列四个命题:
是一条直线,给出下列四个命题:
①若 ,则
,则 ;
②若
;
②若 ,则
,则 ;
;
③若 上有两个点到
上有两个点到 的距离相等,则
的距离相等,则 ; ④若
; ④若 ,则
,则 。
。
其中正确命题的序号是
4、 =
=
5、已知点A、B、C满足 ,
, ,
, ,则
,则 的值是_____________.
的值是_____________.
6、若数列 的前
的前 项和
项和 ,则数列
,则数列 中数值最小的项是第 项.
中数值最小的项是第 项.
7、棱长为1的正方体 的8个顶点都在球
的8个顶点都在球 的表面上,
的表面上, 分别是棱
分别是棱 ,
, 的 中点,则直线
的 中点,则直线 被球
被球 截得的线段长为
截得的线段长为
8、设 分别是椭圆
分别是椭圆 (
( )的左、右焦点,若在其右准线上存在
)的左、右焦点,若在其右准线上存在 使线段
使线段 的中垂线过点
的中垂线过点 ,则椭圆离心率的取值范围是
,则椭圆离心率的取值范围是
9、实数 满足
满足 ,且
,且 ,则
,则
10、已知 直线
直线 和直线
和直线 与两坐标轴;围成一个 四边形,则使得这个四边形面积最小的
与两坐标轴;围成一个 四边形,则使得这个四边形面积最小的 值为
值为
11、正三棱锥 高为2,侧棱与底面成
高为2,侧棱与底面成 角,则点A到侧面
角,则点A到侧面 的距离是
的距离是
12、已知O为坐标原点,  集合
集合

且

13、已知 是以2为周期的偶函数,当
是以2为周期的偶函数,当 时,
时, ,且在
,且在 内,关于
内,关于 的方程
的方程 有四个根,则
有四个根,则 得取值范围是
得取值范围是
14、已知点 (1,0)在直线
(1,0)在直线 的两侧,则下列说法
的两侧,则下列说法
(1)
(2) 时,
时, 有最小值,无最大值
有最小值,无最大值
(3) 恒成立
恒成立
(4)
 ,
, ,
则
,
则 的取值范围为(-
的取值范围为(-
其中正确的是
(把你认为所有正确的命题的序号都填上)
二、解答题:本大题共6小题,共90分.解答时应写出文字说明、证明过程或演算步骤.
15、已知向量a=(3sinα,cosα),b=(2sinα, 5sinα-4cosα),α∈( ),且a⊥b.
),且a⊥b.
(1)求tanα的值;
试题详情
(2)求cos( )的值.
)的值.
试题详情
试题详情
(1)求证: //平面
//平面 ;
;
试题详情
 (2)求证:
(2)求证: ;
;
试题详情
(3)求三棱锥 的体积.
的体积.
试题详情
试题详情
试题详情
18、如图,公园有一块边长为2的等边△ABC的边角地,现修成草坪,图中DE把草坪分成面积相等的两部分,D在AB上,E在AC上.
(1)设AD=x(x≥0),ED=y,求用x表示y的函数关系式;
(2)如果DE是灌溉水管,为节约成本,希望它最短,DE的位置应在哪里?如果DE是参观线路,则希望它最长,DE的位置又应在哪里?请予证明
试题详情
试题详情
试题详情
 的一个极值点.
的一个极值点.
试题详情
(1)求数列 的通项公式;
的通项公式;
试题详情
试题详情
 对任意
对任意 都成立.
都成立.
试题详情
试题详情
(1)讨论 时,
时,  的单调性、极值;
的单调性、极值;
试题详情
(2)求证:在(1)的条件下,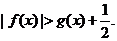
试题详情
(3)是否存在实数 ,使
,使 的最小值是3,如果存在,求出
的最小值是3,如果存在,求出 的值;如果不存在,说明理由。
的值;如果不存在,说明理由。
理科加试题
试题详情
1、在一次抗洪抢险中,准备用射击的方法引爆从桥上游漂流而下的一巨大汽油罐.已知只有5发子弹备用,且首次命中只能使汽油流出,再次命中才能引爆成功,每次射击命中率都是 .,每次命中与否互相独立.
.,每次命中与否互相独立.
(1) 求油罐被引爆的概率.
(2) 如果引爆或子弹打光则停止射击,设射击次数为ξ,求ξ的分布列及ξ的数学期望
试题详情
试题详情
 (1)求
(1)求 、b、c的值
、b、c的值
(2)求阴影面积S关于t的函数S(t)的解析式;
试题详情
3、选修4-2:矩阵与变换
在直角坐标系中,已知△ABC的顶点坐标为A(0,0)、B(1,1)、C(0,2),求△ABC在矩阵MN作用下变换所得到的图形的面积
试题详情
试题详情
试题详情
试题详情
(1)把 和
和 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
试题详情
(2)求经过 ,
, 交点的直线的直角坐标方程.
交点的直线的直角坐标方程.
试题详情
一、填空题
1、 2、40 3、② ④) 4、-1 5、
2、40 3、② ④) 4、-1 5、 6、3
6、3
7、 8、
8、 9、1 10、
9、1 10、 11、
11、 12、46 13、
12、46 13、
14、(3)(4)
二、解答题
15、解:(1)∵a⊥b,∴a?b=0.而a=(3sinα,cosα),b=(2sinα, 5sinα-4cosα),
故a?b=6sin2α+5sinαcosα-4cos2α=0.……………………………………2分
由于cosα≠0,∴6tan2α+5tanα-4 =0.解之,得tanα=- ,或tanα=
,或tanα= .……………………………………………6分
.……………………………………………6分
∵α∈( ),tanα<0,故tanα=
),tanα<0,故tanα= (舍去).∴tanα=-
(舍去).∴tanα=- .…………7分
.…………7分
(2)∵α∈( ),∴
),∴ .
.
由tanα=- ,求得
,求得 ,
, =2(舍去).
=2(舍去).
∴ ,…………………………………………………………12分
,…………………………………………………………12分
cos( )=
)=
= =
= . ………………………14分
. ………………………14分
16、证明:(1)连结 ,在
,在 中,
中, 、
、 分别为
分别为 ,
, 的中点,则
的中点,则


(2)





(3)
 且
且 
 ,
,

∴ 即
即
 =
=
=
17、解:由已知圆的方程为 ,
,
按 平移得到
平移得到 .
.
∵ ∴
∴ .
.
即 .
.
又 ,且
,且 ,∴
,∴ .∴
.∴ .
.
设 ,
,  的中点为D.
的中点为D.
由 ,则
,则 ,又
,又 .
.
∴ 到
到 的距离等于
的距离等于 .
.
即 , ∴
, ∴ .
.
∴直线 的方程为:
的方程为: 或
或 .
.
18、(1)在△ADE中,y2=x2+AE2-2x?AE?cos60° y2=x2+AE2-x?AE,①
y2=x2+AE2-x?AE,①
又S△ADE= S△ABC=
S△ABC= a2=
a2= x?AE?sin60°
x?AE?sin60° x?AE=2.②
x?AE=2.②
②代入①得y2=x2+ -2(y>0), ∴y=
-2(y>0), ∴y= (1≤x≤2)。。。.6分
(1≤x≤2)。。。.6分
(2)如果DE是水管y= ≥
≥ ,
,
当且仅当x2= ,即x=
,即x= 时“=”成立,故DE∥BC,且DE=
时“=”成立,故DE∥BC,且DE= .
.
如果DE是参观线路,记f(x)=x2+ ,可知
,可知
函数在[1, ]上递减,在[
]上递减,在[ ,2]上递增,
,2]上递增,
故f(x) max=f(1)=f(2)=5. ∴y max= .
.
即DE为AB中线或AC中线时,DE最长.。。。。。。。。。。。8分
19、解:(1)由
 是首项为
是首项为 ,公比为
,公比为 的等比数列
的等比数列
当 时,
时, ,
,
所以 
(2)由 得:
得:
 (作差证明)
(作差证明)

综上所述当 时,不等式
时,不等式 对任意
对任意 都成立.
都成立.
20.解.(1)


 当
当 时,
时, ,此时
,此时 为单调递减
为单调递减
当 时,
时, ,此时
,此时 为单调递增
为单调递增

 的极小值为
的极小值为
(2)
 的极小值,即
的极小值,即 在
在 的最小值为1
的最小值为1

 令
令
又
 当
当 时
时
 在
在 上单调递减
上单调递减


 当
当 时,
时,
(3)假设存在实数 ,使
,使 有最小值3,
有最小值3,

①当 时,由于
时,由于 ,则
,则
 函数
函数 是
是 上的增函数
上的增函数


解得 (舍去)
(舍去)
②当 时,则当
时,则当 时,
时,
此时 是减函数
是减函数
当 时,
时, ,此时
,此时 是增函数
是增函数


解得
理科加试题
1、(1)“油罐被引爆”的事件为事件A,其对立事件为 ,则P(
,则P( )=C
)=C
∴P(A)=1- 答:油罐被引爆的概率为
答:油罐被引爆的概率为
(2)射击次数ξ的可能取值为2,3,4,5,
P(ξ=2)= , P(ξ=3)=C
, P(ξ=3)=C ,
,
P(ξ=4)=C , P(ξ=5)=C
, P(ξ=5)=C
ξ
2
3
4
5
P




故ξ的分布列为:
Eξ=2× +3×
+3× +4×
+4× +5×
+5× =
=
2、解:(1)由图形可知二次函数的图象过点(0,0),(8,0),并且f(x)的最大值为16
则 ,
,
∴函数f(x)的解析式为
(2)由 得
得
∵0≤t≤2,∴直线l1与f(x)的图象的交点坐标为(
由定积分的几何意义知:



3、解:在矩阵N=
 的作用下,一个图形变换为其绕原点逆时针旋转
的作用下,一个图形变换为其绕原点逆时针旋转 得到的图形,在矩阵M=
得到的图形,在矩阵M=
 的作用下,一个图形变换为与之关于直线
的作用下,一个图形变换为与之关于直线 对称的图形。因此
对称的图形。因此
△ABC在矩阵MN作用下变换所得到的图形与△ABC全等,从而其面积等于△ABC的面积,即为1
4、解:以极点为原点,极轴为 轴正半轴,建立平面直角坐标系,两坐标系中取相同的长度单位.
轴正半轴,建立平面直角坐标系,两坐标系中取相同的长度单位.
(1) ,
, ,由
,由 得
得 .
.
所以 .
.
即 为
为 的直角坐标方程.
的直角坐标方程.
同理 为
为 的直角坐标方程.
的直角坐标方程.
(2)由
 解得
解得
 .
.
即 ,
, 交于点
交于点 和
和 .过交点的直线的直角坐标方程为
.过交点的直线的直角坐标方程为 .
.
