|
试题详情
试题详情
7.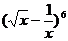 的展开式中常数项等于 ( ) 的展开式中常数项等于 ( ) 试题详情
A.15 B.-15 C.20 D.-20 试题详情
8.平面内有两个定点A、B,动点P满足|AP|=2|PB|,则点P的轨迹是 ( ) 试题详情
A.直线 B.双曲线 C.椭圆 D.圆 试题详情
9.已知定义在R上的偶函数f(x)满足f(x+2)=- f(x),则f(9)的值为 ( ) 试题详情
A.-1 B.0 C.1 D.2 试题详情
10.将4个不同颜色的小球全部放入不同标号的3个盒子中,可以有一个或者多个盒子空着 试题详情
的放法种数为 ( ) 试题详情
A.96 B.36 C.64 D.81 试题详情
11.已知各顶点都在同一个球面上的正四棱锥高为3,体积为6,则这个球的表面积是( ) 试题详情
A.13π B.17π C.21π D.25π 试题详情
12.已知点A(2,2),P为双曲线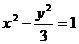 上一动点,F为双曲线的右焦点 上一动点,F为双曲线的右焦点 试题详情
则|PA|+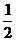 |PF|的最小值为 ( ) |PF|的最小值为 ( ) 试题详情
试题详情
 第Ⅱ卷(非选择题,共90分) 第Ⅱ卷(非选择题,共90分)
试题详情
试题详情
二、填空题(本大题共4小题,每小题5分,共20分,把正确答案填在题中横线上)
试题详情
14.将直线l按向量a=(2,-1)平移后得到直线l′,再将直线l′按向量b=(-1,2)平移 试题详情
后又与直线l重合,则直线l的斜率为
。 试题详情
试题详情
试题详情
16.已知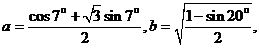 ,则a、b、c的大小关系为
。 ,则a、b、c的大小关系为
。 试题详情
三、解答题(本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤) 17.(本小题满分10分) 试题详情
已知函数  试题详情
(1)求函数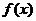 的单调增区间; 的单调增区间; 试题详情
(2)求函数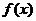 的最值及取得最值时x的值。 的最值及取得最值时x的值。 试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
18.(本小题满分12分) 试题详情
在△ABC中,a、b、c分别是角A、B、C所对的边,已知  试题详情
(1)判断△ABC的形状; 试题详情
(2)若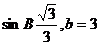 ,求△ABC的面积。 ,求△ABC的面积。 试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
19.(本小题满分12分) 试题详情
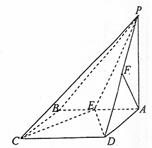 如图,四棱锥P―ABCD的底面是正方形,PA⊥底面ABCD,PA=2,∠PDA=45°,点 如图,四棱锥P―ABCD的底面是正方形,PA⊥底面ABCD,PA=2,∠PDA=45°,点
试题详情
E、F分别为棱AB、PD的中点。 试题详情
(1)求证:AF∥平面PCE; 试题详情
(2)求二面角E―PD―C的大小; 试题详情
(3)求点A到平面PCE的距离。 试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
20.(本小题满分12分) 试题详情
试题详情
(1)求证:数列{bn}为等比数列; 试题详情
(2)求an及Sn; 试题详情
(3)设cn= Sn+nan,Tn为数列{cn}的前n项和,求证:Tn<1. 试题详情
试题详情
试题详情
21.(本小题满分12分) 设f(x)=ax2+bx+c,若6a+2b+c=0,f(1)f(3)>0, (1)求证:a=1,求f(2)的值; (2)求证:方程f(x)=0必有两个不等实根x1、x2,且3<x1+ x2<5。 试题详情
22.(本小题满分12分) 已知直线l:y=x+b交曲线C:y=x2(a>0)于P、Q两点,M为PQ中点,分别过P、 Q两点作曲线C的切线,两切线交于点N,当b变化时。
(1)求点M的轨迹方程;
(2)求点N的轨迹方程;
(3)求证:MN中点必在曲线C上。 数 学 参 考 答 案(文) 第Ⅰ卷 (选择题,共60分) 试题详情
一、选择题(每小题5分,共60分) 1.B 2.C 3.D 4.C 5.B 6.A 7.A 8.D 9.B 10.D 11.A 12.C 简答与提示: 试题详情
1.∵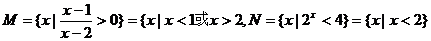 , , 试题详情
∴M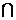 N=(- N=(-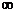 ,1),故选B ,1),故选B 试题详情
2.∵ 试题详情
∴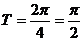 ,故选C。 ,故选C。 试题详情
3.取a=1,b=-2,可验证A、B、C均不正确,故选D。 试题详情
4.垂直于同一直线的两条直线不一定平行,可能相交或异面,故选C。 试题详情
试题详情
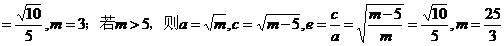 ,故 ,故
选B。 试题详情
6.∵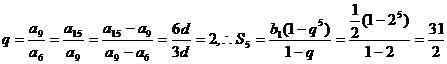 ,故选A。 ,故选A。 试题详情
7.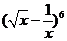 的展开式中常数项为第3项, 的展开式中常数项为第3项,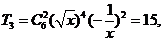 故选A。 故选A。 试题详情
8.可建立平面直角坐标系求出轨迹方程,根据方程形式可判断轨迹为圆,或由平面几何中
相关定理可知轨迹是圆,故选D。 试题详情
9.由f(x+2)=- f(x)可得f(x+4)=- f(x+2)= f(x),所以函数f(x)为周期函数,最小
正周期为T=4,f(9)= f(1)=- f(-1),又函数f(x)为偶函数,所以f(1)= f(-1)=0,所以f(9)=0,故选B。 试题详情
试题详情
11.由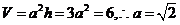 ∴正四棱柱的体对角线l= ∴正四棱柱的体对角线l=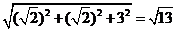 , , 试题详情
∴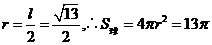 故选A。 故选A。 试题详情
12.根据双曲线第二定义,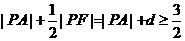 (其中d表示点P到右准线的距离,)故选C。 (其中d表示点P到右准线的距离,)故选C。 第Ⅱ卷(非选择题,共90分) 试题详情
二、填空题(每小题5分,共20分)
试题详情
 简答与提示: 简答与提示:
试题详情
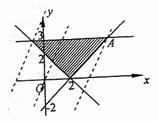
13.画出可行域,如右图所示,在点A(5,3)处取得 试题详情
试题详情
14.设直线l方程为y=kx+b,按向量a=(2,-1)平移 试题详情
后得到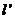 按向量b=(-1,2)平移后得直线方程为 按向量b=(-1,2)平移后得直线方程为 试题详情
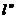 :y=k:y=k(x-2)+b-1再将 :y=k:y=k(x-2)+b-1再将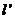 (x+1-2)+b-1+2=kx-k+b+1, (x+1-2)+b-1+2=kx-k+b+1, 试题详情
试题详情
15.∵ 试题详情
16.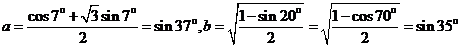 ,∴a>b。 ,∴a>b。 试题详情
三、解答题(本大题共6小题,共70分) 17.解:本小题主要考查三角恒等变换及三角函数图象和性质。 试题详情
(1) 试题详情
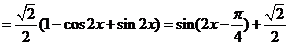 (4分) (4分) 试题详情
∴当 试题详情
即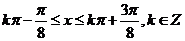 时,函数 时,函数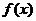 为增函数, 为增函数, 试题详情
∴增区间为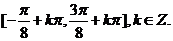 (6分) (6分) 试题详情
试题详情
试题详情
18.本小题主要考查正余弦定理的应用及三角恒等变换。 试题详情
解:(1)∵ 试题详情
∴ ∴sinA=2cosBsinC, 又∵sinA=sin[π-(B+C)]=sin(B+C)=sinBcosC+cosBsinC, ∴sinBcosC+
cosBsinC=2cosBsinC, ∴sinBcosC-
cosBsinC= sin(B-C)=0 ∴在△ABC中B=C, ∴△ABC为等腰三角形 试题详情
另解:∵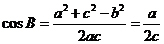 , , ∴a2+c2-b2=a2, ∴c2=b2 ∴c=b ∴△ABC为等腰三角形 试题详情
(2)∵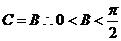 , , 试题详情
∵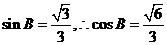 , , 试题详情
∴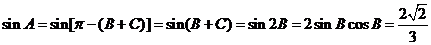 , , 试题详情
∴ 。 (12分) 。 (12分) 另解:b=3,∴c=b=3 试题详情
又∵ 试题详情
∴ 试题详情
∴ 试题详情
19.本小题主要考查空间线面关系,空间想象能力和推理运算能力或空间向量的应用。 解法一: (1)证明: 试题详情
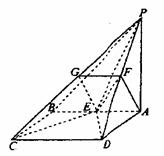 取PC的中点G,连接FG、EG, 取PC的中点G,连接FG、EG,
∴FG为△PCD且FG∥CD, 试题详情
∴FG=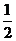 CD且FG∥CD, CD且FG∥CD, 又∵底面四边形ABCD是正方形,E为棱AB的中点, 试题详情
∴AE=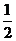 CD且AE∥CD, CD且AE∥CD, ∴AE=FG且AE∥FG, ∴四边形AEGF是平行四边形, ∴AF∥EG, 试题详情
又EG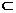 平面PCE,AF 平面PCE,AF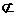 平面PCE, (4分) 平面PCE, (4分) ∴AF∥平面PCE。 (2)∵PA⊥底面ABCD, ∴PA⊥AD,PA⊥CD, 试题详情
又AD⊥CD,PA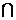 AD=A, AD=A, ∴CD⊥平面PAD,∴CD⊥AF 试题详情
又PA=2,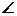 PDA=45°, PDA=45°, ∴PA=AD=2, ∵F是PD的中点,∴AF⊥PD, 试题详情
又CD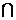 PD=D, PD=D, ∴AF⊥平面PCD, ∵AF∥EG, ∴EG⊥平面PCD, 又GF⊥PD,连结EF, 试题详情
则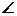 GFE是二面角E―PD―C的平面角。 (6分) GFE是二面角E―PD―C的平面角。 (6分) 试题详情
在Rt△EGF中,EG=AF= ,GF=1, ,GF=1, 试题详情
∴tan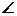 GFE= GFE= 试题详情
∴二面角E―PD―C的大小为arctan 。 (8分) 。 (8分) (3)设A到平面PCE的距离为h, 试题详情
由 试题详情
∴点A到平面PCE的距离为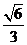 解法二: (1)由于PA⊥底面ABCD,且底面四边形ABCD是正方形,以A为坐标原点建立空间 直角坐标系如图, 试题详情
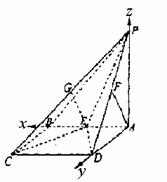 ∵PA=2,, ∵PA=2,,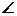 PDA=45°,∴AD=AB=PA=2, PDA=45°,∴AD=AB=PA=2,
∴A(0,0,0),B(2,0,0), C(2,2,0), D(0,2,0), P(0,0,2) ∵点E、F分别为棱AB、PD的中点, ∴E(1,0,0),F(0,1,1),取 PC的中点G,连结EG,则G(1,1,1), 试题详情
∴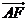 (0,1,1), (0,1,1),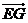 =(0,1,1), =(0,1,1), ∴AF∥EG, 试题详情
又∵EG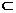 平面PCE,AF 平面PCE,AF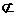 PCE, PCE, ∴AF∥平面PCE。 (4分) 试题详情
(2)设平面PDE的法向量为 试题详情
∵ 试题详情
∴ 试题详情
设平面PCD的法向量为 试题详情
∵ 试题详情
∴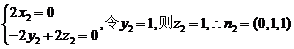 (6分) (6分) 试题详情
∴ 试题详情
∴二面角E―PD―C的大小为arccos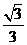 。 (8分) 。 (8分) 试题详情
(3)设平面PCE的法向量 试题详情
∵ 试题详情
∴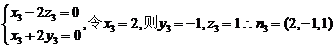 (10分) (10分) 试题详情
∵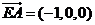 ,∴点A到平面PCE的距离 ,∴点A到平面PCE的距离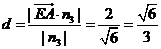 (12分) (12分) 试题详情
20.本小题主要考查利用递推关系求通项公式的方法错位相减法求和。 试题详情
(1)∵ 试题详情
∴ 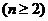 (2分) (2分) 试题详情
∴ 试题详情
试题详情
又由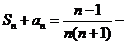 得 得 试题详情
∴{bn}是以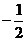 为首项,以 为首项,以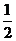 为公比的等比数列。 (5分) 为公比的等比数列。 (5分) 试题详情
(2)由(1)知数列{bn}是以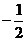 为首项,以 为首项,以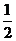 为公比的等比数列, 为公比的等比数列, 试题详情
∴ 试题详情
∴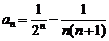 。 (8分) 。 (8分) 试题详情
(3) 试题详情
试题详情
试题详情
∴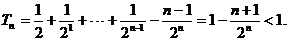 (12分) (12分) 试题详情
21.本小题主要考查二次函数图象及性质,二次函数、二次方程、二次不等式的关系。 解:(1)∵6a+2b+c=0,a=1 试题详情
∴f(2)=4a+2b+c=-2a=-2. (4分)
(2)首先说明a≠0, ∵f(1)f(3)=(a+b+c)(9a+3b+c)=―(5a+b)(3a+b)>0, 若a=0,则f(1)f(3)=-b2<0与已知矛盾, ∴a≠0, (6分) 其次说明二次方程f(x)=0必有两个不等实根,x1、x2, ∵f(2)=4a+2b+c=-2a ∴若a>0,二次函数f(x)=ax2+bx+c开口向上,而此时f(2)<0 ∴若a<0,二次函数f(x)=ax2+bx+c开口向下,而此时f(2)>0 故二次函数图象必于x轴有两个不同交点, ∴二次方程f(x)=0必有两个不等实根,x1、x2, 试题详情
(或利用△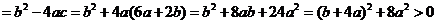 来说 来说 明) (9分) ∵a≠0, ∴将不等式-(5a+b)(3a+b)两边同除以-a2得 试题详情
试题详情
∴ 试题详情
∴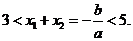 (12分) (12分) 试题详情
22.本小题主要考查直线与抛物线位置关系及弦中点问题,轨迹的求法。
(1)设P(x1,y1),Q(x2,y2) 试题详情
由 试题详情
∴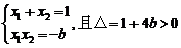 (2分) (2分) 试题详情
∴ 试题详情
∴ 试题详情
∴点M的轨迹方程为直线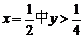 部分 (4分) 部分 (4分)
(2)设以点P(x1,y1)为切点的曲线C的切线方程l1:y-y1= k1(x-x1) 将l1方程代入曲线C:y=x2并整理得 x2-
k1x-y1+k1x1=0, 试题详情
△= ∴k1=2x1,(也可利用导数直接得出此结论)。 (6分) ∴直线l1方程可化为y=2x1x-x12 ① 同理,以Q为切点的切线l2方程可化为y=2x2x-x22 ②, 试题详情
由①②可解出交点N坐标, = = 试题详情
∴点N的轨迹方程为直线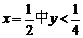 (10分) (10分) 试题详情
(3)由(1)知点M的坐标为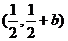 由(2)知道点N坐标为 由(2)知道点N坐标为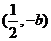 , , 试题详情
∴MN中点坐标为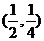 ,满足曲线C的方程, ,满足曲线C的方程, ∴MN中点必在曲线C上。 (12分) 试题详情
| 










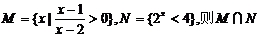 ( )
( )
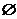 B.(-∞,1) C.(1,2) D.(-∞,2)
B.(-∞,1) C.(1,2) D.(-∞,2)
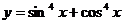 的最小正周期为 ( )
的最小正周期为 ( )
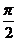 B.2π C.π D.
B.2π C.π D.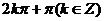


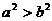 B.
B.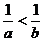 C.lga>lgb D.
C.lga>lgb D.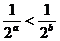






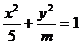 的离心率
的离心率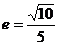 ,则m的值为 ( )
,则m的值为 ( )
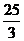 C.
C.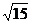 D.
D.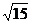 或
或