
2009年石家庄市高中毕业班第二次模拟考试试卷
数学(理科)答案
一、A卷选择题:本大题共12小题,每小题5分,共60分.
1.C 2. B 3. B 4. D 5.D 6.A
7. A 8.C 9. B 10. A 11.C 12.C
一、B卷选择题:本大题共12小题,每小题5分,共60分.
1.B 2. C 3. C 4. D 5.D 6.A
7. A 8.B 9. C 10. A 11.B 12.B
二、填空题:本大题共4小题,每小题5分,共20分
13.20 14.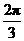
15.
 16.
16.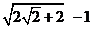
三、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.
17.解:(Ⅰ)依题意,


 ……………………3分
……………………3分
∵函数 的图象的相邻两条对称轴之间的距离是
的图象的相邻两条对称轴之间的距离是 ,
,
∴函数 的最小正周期为
的最小正周期为 ,又
,又 >0,
>0,
∴ ,解得
,解得 =1.
…………………………6分
=1.
…………………………6分
(Ⅱ)由(Ⅰ)可知,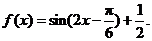
依题意, ≤2
≤2
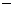
 ≤
≤ ,…………………8分
,…………………8分
所以 ≤
≤ ≤
≤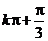 ,
,
所以函数 的单调递增区间为[
的单调递增区间为[ ,
, 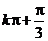 ],
], . ……………10分
. ……………10分
 18. 解:(Ⅰ)依题意
18. 解:(Ⅰ)依题意 平行且等于
平行且等于 ,
,

 //
// ,又
,又



依题意,  .
.

 平面
平面 ,
,

 平面
平面 .……………3分
.……………3分


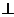
 ,
,
可知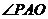 为二面角
为二面角 的平面角,
的平面角,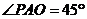 .
.
 ,
, ,即
,即 .
.
所以 平面
平面 .……………6分
.……………6分
(II)延长 ,
, 交于E,连结
交于E,连结 ,
, .
.
由(Ⅰ)可知, 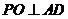 ,又
,又 ,
,


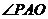 .
.
 ,由(Ⅰ)可知,
,由(Ⅰ)可知,  .
.
 平面
平面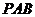 .
.
 为直线
为直线 与平面
与平面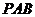 所成的角. ……………9分
所成的角. ……………9分
 在直角三角形
在直角三角形 中,
中,  ,
,
 ……………12分
……………12分
19. 解:(Ⅰ)依题意知 ,故
,故 =
= ,∴
,∴ =
= .…………4分
.…………4分
(Ⅱ) 的取值可以是0,1,2.
的取值可以是0,1,2.
设甲两次试跳成功的次数为 ,
,
 (
( =0)=
=0)=  +
+  +
+ 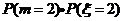
=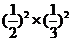 +
+ +
+
= .
…………6分
.
…………6分
 (
( =2)=
=2)=  +
+ =
=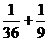 =
= .
.
∴ (
( =1)=1
=1)=1 (
( =0)
=0) (
( =2)=
=2)= . ………9分
. ………9分
故 的分布列是
的分布列是

0
1
2




………10分
E =
= .…………12分
.…………12分
20.解:(Ⅰ)  ……………………3分
……………………3分
∵函数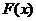 的图象在
的图象在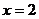 处的切线平行于x轴,
处的切线平行于x轴,

 ,
,
解得 .………………………………………………………………5分
.………………………………………………………………5分
(Ⅱ)由(Ⅰ)可知,
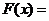

 ……………………6分
……………………6分
令

∴当 时,
时, ,当
,当 时,
时, .
.
∴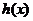 在
在 上是单调减函数,在
上是单调减函数,在 上是单调增函数.
上是单调增函数.
 ,
, .…………………………8分
.…………………………8分
∴当 时,有
时,有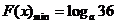 ,当
,当 时,有
时,有 .
.
∵当 时,
时, 恒成立, ∴
恒成立, ∴ …………………………10分
…………………………10分
∴可列 ①,或
①,或 ②
②
不等式组①的解集为空集,不等式组②得
综上所述, 的取值范围是:
的取值范围是: .. ……………………12分.
.. ……………………12分.
解法二:由于对任意的 ,都有
,都有 成立,
成立,
所以 ,即
,即 ,可得
,可得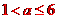 .…………7分
.…………7分
于是 可化为
可化为 .
.
当 时,
时, .
.
即 最小值是32. (当
最小值是32. (当 时,上式取等号) …………9分
时,上式取等号) …………9分
所以 ,又
,又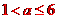 ,所以
,所以 .
.
所以 的取值范围是
的取值范围是 …………12分
…………12分
21.解:(Ⅰ)由 可得
可得 …………2分
…………2分
由 解得
解得 ,
,
依题意, ,
,

所以双曲线C的方程为 …………5分
…………5分
(Ⅱ)
(?)若直线l的斜率不存在,由双曲线的对称性可知,双曲线C实轴上的任何点都适合题意. …………………6分
(?)若直线l的斜率存在,设直线l的方程为y=k(x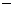 3),
3),
设P(x1,y1),Q(x2,y2),N (t,0)
由 得
得 ,
,
∵直线l与双曲线C的右支交于P、Q两点,
∴
解得k> 或k<
或k<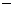
 . ………………9分
. ………………9分
∵∠PNF=∠QNF,∴KNP=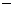 KNQ. …………………10分
KNQ. …………………10分
∴ ∴
∴
即2x1x2-(t+3)(x1+x2)+6t=0,
将x1+x2=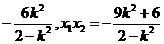 代入上式,整理得t=1.
代入上式,整理得t=1.
综上所述::存在点N满足条件,点N的坐标是N(1,0). …………12分
22.解:(?)当 时,
时, ,
,
 ,
,
可得: ,
,
 .…………2分
.…………2分


可得, …………4分
…………4分
(?)(1)当n=2时, 不等式成立. …………5分
不等式成立. …………5分
(2)假设当 时,不等式成立,即
时,不等式成立,即 .
.
那么,当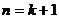 时,
时,
 ,所以当
,所以当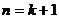 时,不等式也成立.
时,不等式也成立.
根据(1),(2)可知,当 时,
时, .…………8分
.…………8分
(?)设 …………9分
…………9分



 上单调递减,
上单调递减,
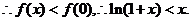
因为当 时,
时,  …………10分
…………10分


 .…………12分
.…………12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com