
A.A受到B的摩擦力沿斜面方向向上。 B.A受到B的摩擦力沿斜面方向向下。 C.A、B之间的摩擦力为零。 D.A、B之间是否存在摩擦力取决于A、B表面的性质,
图17
试题详情
试题详情
2.用质量为m、长度为L的绳沿着光滑水平面拉动质量为M的物体,在绳的一端所施加的水平拉力为F, 如图18所示,求: (1)物体与绳的加速度; (2)绳中各处张力的大小(假定绳的质量分布均匀,下垂度可忽略不计。) 试题详情
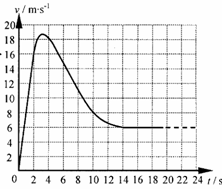
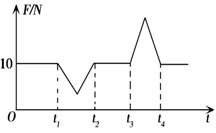 3.某实验小组的同学在电梯的天花板上固定一根弹簧秤,使其测量挂钩向下,并在钩上悬挂一个重为10N的钩码.弹簧秤弹力随时间变化的规律可通过一传感器直接得出,如图19所示,则下列分析正确的是( ) 3.某实验小组的同学在电梯的天花板上固定一根弹簧秤,使其测量挂钩向下,并在钩上悬挂一个重为10N的钩码.弹簧秤弹力随时间变化的规律可通过一传感器直接得出,如图19所示,则下列分析正确的是( )
A.从时刻t1到t2,钩码处于失重状态 B.从时刻t3到t4,钩码处于超重状态
C.电梯可能开始在15楼,先加速向下,接着匀速向下,再减速向下,最后停在1楼 试题详情
D.电梯可能开始在1楼,先加速向下,接着匀速向上,再减速向上,最后停在15楼
图19 试题详情
4.如图20所示为汽车刹车痕迹长度x(即刹车距离)与刹车前车速v(汽车刹车前匀速行驶)的关系图象。例如,当刹车痕迹长度为40m时,刹车前车速为80km/h (1)假设刹车时,车轮立即停止转动,尝试用你学过的知识定量推导并说明刹车痕迹与刹车前车速的关系。 (2)在处理一次交通事故时,交警根据汽车损坏程度 估计出碰撞时的车速为40km/h,并且已测出刹车痕迹长度 试题详情
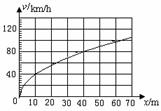 为20m,请你根据图象帮助交警确定出该汽车刹车前的车速,并在图象中的纵轴上用字母A标出这一速度,由图象 为20m,请你根据图象帮助交警确定出该汽车刹车前的车速,并在图象中的纵轴上用字母A标出这一速度,由图象
知,汽车刹车前的速度为多少?
图20 试题详情
5.飞机沿水平方向前进时,升力与飞机的速度大小成正比,比例系数为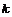 ,假设飞机起飞过程中获得的牵引力是恒定的,要想使质量为 ,假设飞机起飞过程中获得的牵引力是恒定的,要想使质量为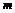 的飞机在长为 的飞机在长为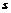 的跑道上完成起飞,请问飞机的牵引力至少是多大?(忽略一切运动阻力) 的跑道上完成起飞,请问飞机的牵引力至少是多大?(忽略一切运动阻力) 试题详情
试题详情
(1)当座舱落到离地面高度为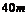 的位置时,铅球对手的作用力多大? 的位置时,铅球对手的作用力多大? 试题详情
(2)当座舱落到离地面高度为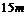 的位置时,手要用多大的力才能托住铅球?( 的位置时,手要用多大的力才能托住铅球?(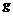 取 取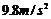 ) ) 试题详情
试题详情
(1)当座舱落到离地面高度为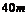 的位置时,铅球对手的作用力多大? 的位置时,铅球对手的作用力多大? 试题详情
(2)当座舱落到离地面高度为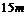 的位置时,手要用多大的力才能托住铅球? 的位置时,手要用多大的力才能托住铅球? 试题详情
(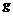 取 取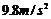 ) ) 试题详情
7.一根均匀的米尺,质量为0.2kg,放在水平桌面上,它与桌面间的动摩擦因数为0.16,有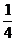 长度露在桌外,现有一水平拉力沿着米尺方向作用在米尺上作用1S,为使米尺能从桌边落下,外力F至少应为多少? 长度露在桌外,现有一水平拉力沿着米尺方向作用在米尺上作用1S,为使米尺能从桌边落下,外力F至少应为多少? 试题详情
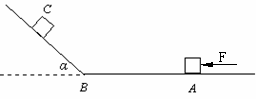
8.如图21所示,在光滑水平面AB上,水平恒力F推动质量为 m=1kg的物体从A点由静止开始作匀加速直线运动,物体到达 B点时撤去 F,接着又冲上光滑斜面(设经过B点前后速度大小不变),最高能到达C点.用速度传感器测量物体的瞬时速度,并在表格中记录了部分测量数据.求:(g取10m/s2) t/s 试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
 (2)斜面的倾角 (2)斜面的倾角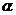 ; ;
试题详情
试题详情
试题详情
试题详情
高考真题 1.【解析】物体从阻力很小的斜面从静止开始滚下时,由牛顿第二定律可得加速度a=gsinθ 是一个定值,再由匀变度直线运动速度公式可得v=at 【答案】B 2.【解析】依题意,若两物体依然相对静止,则a的加速度一 定水平向右,如图将加速度分解为垂直斜面与平行于斜面,则垂直斜面方向,N-mgcosθ=may,即支持力N大于mgcosθ,与都静止时比较,a与b间的压力增大;沿着斜面方向,若加速度a过大,则摩擦力可能沿着斜面向下,即a物块可能相对b向上滑动趋势,甚至相对向上滑动,故A错,B、C正确;对系统整体,在竖直方向,若物块a相对b向上滑动,则a还具有向上的分加速度,即对整体的牛顿第二定律可知,系统处于超重状态,b与地面之间的压力将大于两物体重力之和,D错。 【答案】BC 3.【解析】如图所示,设绳中张力为T,A、B、C共同的加速度为a,与C相连部分的绳与竖直线夹角为α,由牛顿运动定律,对A、B、C 组成的整体有 F=3ma …① 对B有
F-T=ma ② 对C有
Tcosα=mg ③  Tsinα=ma ④
Tsinα=ma ④
联立①②式得:T=2ma…⑤ 联立③④式得: T2=m2(g2+a2)
⑥ 联立⑤⑥式得: ⑦ ⑦ 利用①⑦式得 …… 【答案】 4.【解析】这是一个物体的受力和时间关系的图像,从图像可以看出在前两秒力的方向和运动的方向相同,物体经历了一个加速度逐渐增大的加速运动和加速度逐渐减小的加速运动,2少末速度达到最大,从2秒末开始到4秒末运动的方向没有发生改变而力的方向发生了改变与运动的方向相反,物体又经历了一个加速度逐渐增大的减速运动和加速度逐渐减小的减速的和前2秒运动相反的运动情况,4秒末速度为零,物体的位移达到最大,所以D正确。 【答案】D 5.【解析】(1)从图中可以看邮,在t=2s内运动员做匀加速运动,其加速度大小为  m/s2=8m/s2 m/s2=8m/s2
设此过程中运动员受到的阻力大小为f,根据牛顿第二定律,有mg-f=ma 得 f=m(g-a)=80×(10-8)N=160N (2)从图中估算得出运动员在14s内下落了 39.5×2×2m=158 根据动能定理,有 所以有  =(80×10×158- =(80×10×158- ×80×62)J≈1.25×105J ×80×62)J≈1.25×105J (3)14s后运动员做匀速运动的时间为  s=57s s=57s 运动员从飞机上跳下到着地需要的总时间 t总=t+t′=(14+57)s=71s 【答案】(1)160N (2) (3)71S ) (3)71S ) 6.【解析】因为受到阻力,不是完全失重状态,所以对支持面有压力,A错。由于箱子阻力和下落的速度成二次方关系,最终将匀速运动,受到的压力等于重力,最终匀速运动,BD错,C对。 【答案】C 7.【解析】对小球受力分析,当N为零时,小球的合外力水平向右,加速度向右,故小车可能向右加速运动或向左减速运动,A对C错;当T为零时,小球的合外力水平向左,加速度向左,故小车可能向右减速运动或向左加速运动,B对D错。解题时抓住N、T为零时受力分析的临界条件,小球与车相对静止,说明小球和小车只能有水平的加速度,作为突破口。 【答案】AB 8.【解析】由牛顿第二定律得:mg-f=ma
 抛物后减速下降有:
Δv=a/Δt
解得: 【答案】101kg 9.【解析】由机械能守恒定律得 , , ; ; 物块先在传送带上作匀减速直线运动,运动时间为 , , 通过的位移为 ; ;
物块再在传送带上作匀加速直线运动,其末速度由 得 得 , , 则匀加速直线运动的时间为 ,通过的位移为 ,通过的位移为 ,然后再作匀速运动,其位移为通过的位移为 ,然后再作匀速运动,其位移为通过的位移为 ,匀速运动的时间为 ,匀速运动的时间为 , , 所以物块在传送带上第一次往返所用的时间为 . . 【答案】
10.【解析】此题以直升机取水救火为背景,考查力与运动关系中的匀速和加速直线运动,因直升机沿水平方向匀速飞往水源取水灭火,所以水箱受力平衡,由平衡条件可得  所以 ;直升机返回时,由牛顿第二定律得 ;直升机返回时,由牛顿第二定律得  。联立两式得,水箱中水的质量M= 。联立两式得,水箱中水的质量M=
【答案】M= 名校试题 1.【解析】(1)小球从离开平板车开始至落到地面所用的时间  (2) 小球放到平板车后相对地面静止,小车的加速度为
 小车向右运动的距离为   小于4m,所以小球不会从车的左端掉下.小车向右运动的时间为 小于4m,所以小球不会从车的左端掉下.小车向右运动的时间为  小车向左运动的加速度为  小车向左运动的距离为  小车向左运动的时间为
(3)
小球刚离开平板车瞬间,小车的速度方向向左,大小为  小球离开车子后,车的加速度为  车子向左运动的距离为  从小球轻放上平板车到落地瞬间,平板车的位移大小X= x1 + x2+ x3 =5.175m 【答案】5.175m
2.【解析】(1)当f=mg时,雨点达到最终速度 ,则 ,则 
得
(2)由牛顿第二定律得 , ,
则
解得 ,即 ,即 。 。
【答案】 3.【解析】①    ②落地时速度   【答案】 4.【解析】对薄板由于Mgsin37 ?m(M+m)gcos37 ?m(M+m)gcos37 故滑块在薄板上滑动时,薄板静止不动. 对滑块:在薄板上滑行时加速度a 故滑块在薄板上滑动时,薄板静止不动. 对滑块:在薄板上滑行时加速度a =gsin37 =gsin37 =6m/s =6m/s ,至B点时速度V= ,至B点时速度V= =6m/s。 =6m/s。 滑块由B至C时的加速度a = gsin37 = gsin37 -mgcos37 -mgcos37 =2 m/s =2 m/s ,滑块由B至C用时t,由L ,滑块由B至C用时t,由L =Vt+ =Vt+ a a t t 即t 即t +6t-7=0 解得t=1s +6t-7=0 解得t=1s 对薄板:滑块滑离后才开始运动,加速度a= gsin37 -mgcos37 -mgcos37 =2 m/s =2 m/s ,滑至C端用时t ,滑至C端用时t = = = = s s 故滑块、平板下端B到达斜面底端C的时间差是△t= t -t= -t= -1=1.65s -1=1.65s 【答案】1.65s 5.【解析】(1) 到 到 由动能定理 由动能定理   解得 (2)滑块沿BC段向上运动的加速度大小 滑块做减速运动,速度为0时所用的时间 滑块做减速运动,速度为0时所用的时间   对滑块受力分析:
对滑块受力分析:  所以 所以 后滑块静止在斜面上 后滑块静止在斜面上 由 得 得 【答案】 6.【解析】(1)由图像可知:物体所受摩擦力f=3N 由牛顿第二定律F-f=ma;可得 (2)N=mg=10N,μ
【答案】1kg  7.【解析】(1)米袋在AB上加速时的加速度 米袋的速度达到 =5m/s时,滑行的距离 =5m/s时,滑行的距离 ,因此米加速 ,因此米加速 一段后与传送带一起匀速运动到达B点,到达C点时速度v0=5m/s,设米袋在CD上运动的加速度大小为a,由牛顿第二定律得  代人数据得a=10m/s2 所以,它能上滑的最大距离 … … (2顺斜部分传送带沿顺时针方向转动时,米袋速度减为4m/s之前的加速度为  ………… ………… 速度减为4m / s时上滑位移为 米袋速度等于4m/s时,滑动摩擦力方向改变,由于 ,故米继续向上减速运动… ,故米继续向上减速运动… 米袋速度小于4m/s减为零前的加速度为-  … … 速度减到0时上滑位移为 … … 可见,米袋速度减速到0时,恰好运行到D点。 米袋从C运动到D所用的时间 【答案】  8.【解析】(1)板在摩擦力作用下向右做匀加速运动直至与物块速度相同,此时物块刚到达板的中点,设木板加速度为a1,运动时间为t1, 对木板有
μ1mg = Ma、v = a1t1 ∴t1 =
设在此过程中物块前进位移为s1,板前进位移为s2,则 s1 = vt1、 s2 = t1 又因为s1 - s2 = ,- 由以上几式可得 物块与板间的动摩擦因数μ1= 、板的位移s2 = . (2)设板与桌面间的动摩擦因数为μ2,物块在板上滑行的时间为t2,木板的加速度为a2,对板有 μ1mg ― μ2(m + M) g
= Ma2,
且v = a2t2 解得t2 =  又设物块从板的左端运动到右端的时间为t3,则 vt3 ―t3 = l, t3 = -- 为了使物块能到达板的右端,必须满足
t2 ≥ t3 ? 即 ,则μ2 ≥ ,则μ2 ≥ - - 所以为了使物块能到达板的右端,板与桌面间的摩擦因数μ2 ≥ - - 【答案】 9.【解析】对于启动状态有: 得
得
对于制动状态有: 得
得
(2)电梯匀速运动的速度
从图中读得,电梯匀速上升的时间t2=26s,电梯运动的总时间t=28s 所以总位移 层高
层高
【答案】 10.【解析】(1)电梯在最初加速阶段0~3.0S内加速度为 ,重物受到的支持力为 ,重物受到的支持力为 ,根据牛顿第二定律,得: ,根据牛顿第二定律,得:  
最后减速阶段13.0~19.0s内,重物加速度大小为 ,重物受到的支持力为 ,重物受到的支持力为 ,根据牛顿第二定律,得: ,根据牛顿第二定律,得:    
(2)在三秒末重物的速度: m/s m/s
(3)设在全程内电梯的位移为 ,电梯加速、匀速、减速运动所用的时间为 ,电梯加速、匀速、减速运动所用的时间为 、 、 、 、 ,得: ,得:
 代入数据得: m m
则平均每层楼高为 m=3。16m m=3。16m
【答案】(1)    (2) (2) m/s(3)3。16m m/s(3)3。16m 考点预测题 1.【解析】设斜面C的倾角为 ,以A?B整体为研究对象,由牛顿第二定律求得整体的加速度为a=g ,以A?B整体为研究对象,由牛顿第二定律求得整体的加速度为a=g in in 。假设A。B之间有摩擦力,且为f,再隔离物体B,由牛顿第二定律得: f +m 。假设A。B之间有摩擦力,且为f,再隔离物体B,由牛顿第二定律得: f +m g g in in =m =m a 代入a得f=0 所以选项C正确。 a 代入a得f=0 所以选项C正确。 【答案】C 2.【解析】很显然,求加速度用整体法,求张力用隔离法 (1)以物体和绳整体为研究对象,根据牛顿第二定律可得: F=(M+m)a,解得a=F/(M+m). (2)以物体和靠近物体x长的绳为研究对象,如图20所示。根据牛顿第二定律可得:Fx=(M+mx/L)a=(M+ ) ) . . 由此式可以看出:绳中各处张力的大小是不同的,当x=0时,绳施于物体M的力的大小为 【答案】a=F/(M+m)  3.【解析】此题在电梯上探究物体的失重与超重,通过图象表示弹簧弹力随时间变化的关系,由图可知, 内物体处于静止状态;从时刻t1到t2 内,因弹力小于10N,钩码的合力方向向下,即加速度向下,所以处于失重状态,故选项A正确,同理,选项B对; 内物体处于静止状态;从时刻t1到t2 内,因弹力小于10N,钩码的合力方向向下,即加速度向下,所以处于失重状态,故选项A正确,同理,选项B对; 综合全过程,若物体开始在15楼,由图可知,t1到t2合力向下,则加速向下,t2到t3合力为零,匀速向下,t3到 合力向上,但速度向下,所以减速向下,最后合力为零,物体静止。故选项C也正确。显然D项错。 合力向上,但速度向下,所以减速向下,最后合力为零,物体静止。故选项C也正确。显然D项错。 【答案】AC 4.【解析】本题是一道与交通有关的力学综合试题,考查学生创新应用能力。近年来,此类以实际问题为背景的试题出现的较为频繁。此类试题考查学生综合运用所学知识分析解决物理问题的能力,体现了以能力立意的高考命题指导思想。本题的情景是学生比较熟悉的,涉及到力和运动的关系、运动学、牛顿定律、物理图象等知识点,虽然综合了较多知识点,但难度不大,更加突出“双基”和“主干”,符合近年来高考命题的趋势和要求.
(1)设汽车的质量为m,轮胎与路面间的动摩擦因数为μ, 由牛顿第二定律得, 由运动学公式得, 由运动学公式得, 故 即刹车痕迹与刹车前车速的平方成正比。 即刹车痕迹与刹车前车速的平方成正比。 (2)汽车相撞时的速度为40km/h,从这个速度减到零,汽车还要向前滑行10m,撞前汽车已经滑行20m,所以,如果汽车不相撞,滑行30m停下。滑行30m对应的初速度如图中的A点对应速度。汽车刹车前的速度为68km/h 【答案】(1) (2)68km/h (2)68km/h 5.【解析】完成起飞时,升力的大小等于重力的大小,即  飞机的加速度 飞机的加速度 根据牛顿第二定律得: 【答案】 6.【解析】(1)在离地面高于 时,座舱做自由落体运动,处于完全失重状态,所以铅球对手没有作用力. 时,座舱做自由落体运动,处于完全失重状态,所以铅球对手没有作用力. (2)设座舱自由下降高度为 时的速度为 时的速度为 ,制动时的加速度为 ,制动时的加速度为 ,制动高度为 ,制动高度为 ,由 ,由 得: 得: 联立解得: 根据牛顿运动定律 根据牛顿运动定律 得: 得:  代入数据解得: 代入数据解得: . .
【答案】 7.【解析】解此题的关键有点:一是把米尺抽象为质点模型,其重心在其几何中心;二是正确分析米尺的物理过程,米尺的运动可以分为两个阶段,先做匀加速直线运动,后做匀减速直线运动:三是能正确地理解、分析一个临界状态,,即米尺恰好掉离桌边的临界条件是速度为零。。有较多的同学没有考虑到这一临界状态,认为米尺运动到桌边,且具有向前的速度,实际上这样求的不是最小力,错解反映出学生在把实际问题转化为物理问题的能力欠缺,无法建立正确的物理图景,分析综合能力有待提高, 由牛顿第二定律与匀变速直线运动规律求解 设拉力停止作用时的速度为V,米尺先匀加速度后匀减速运动,由牛顿第二定律,加速阶段:  为加速阶段的加速度) 为加速阶段的加速度)
减速阶段: ( ( 为减速度阶段的加速度) 为减速度阶段的加速度)
由匀变速直线运动规律和几何条件得: 联立以上三式得: 至少为 至少为 。 。 【答案】  至少为 至少为
8.【解析】(1)物体从 A 到 B 过程中: ∴ F=ma1= 2N 。
(2)物体从 B 到 C 过程中:  ∴
∴ 
(3)设B点的速度为vB,在0.4~2.2s时间段内,从v=0.8m/s到 B 点过程,
从B点到v=3m/s 过程,
 解得: 解得:   所以,当 t =2s时物体刚好达到 B 点。 所以,当 t =2s时物体刚好达到 B 点。
当 t=2.1s时,物体在斜面上向上运动,则    【答案】(1)2N (2) 【答案】(1)2N (2) (3) (3)
9.【解析】1)设人跳起后重心离地高度为 ,为完成空中动作, ,为完成空中动作, 必须满足以下条件: 必须满足以下条件:  , ,
(2)设人跳起后从 的高度下落,下蹲过程受力情况如图, 的高度下落,下蹲过程受力情况如图,
人在地面的作用力和重力的作用下作匀变速运动,由第二定律和运动学公式可得以下几式:   解得: 解得: 所以H的范围是: 所以H的范围是: > > > >
【答案】 > > > > 10.【解析】(1)该同学的整个运动过程可分为两个阶段:先是做初速为零的匀加速运动,时间很短,仅为0.45S;对该同学在第二阶段中运用运动学公式,可求得两阶段交界时刻的速度v  m/s m/s 该同学在第一阶段中的加速度为a= m/s m/s 设地面对该同学的支持力 ,由牛顿第二定律有 ,由牛顿第二定律有 mg=ma mg=ma 得 N由牛顿第三定律知,他蹬地的力的大小 N由牛顿第三定律知,他蹬地的力的大小  N N
(2)该问中的整个运动过程可分为四个阶段:第一阶段是下落高度为1.0m的自由下落阶段;第二阶段是减速时间为0.25S的匀减速至停下的缓冲阶段(此阶段人腿弯曲,重心下降);第三阶段是用力 蹬地使身体由弯曲站直的匀加速上升阶段(此阶段重心升高的高度与第二阶段重心下降的高度相等);第四个阶段是离地后竖直向上的匀减运动阶段,上升高度为0.5m。 蹬地使身体由弯曲站直的匀加速上升阶段(此阶段重心升高的高度与第二阶段重心下降的高度相等);第四个阶段是离地后竖直向上的匀减运动阶段,上升高度为0.5m。 第一阶段下落1.0m的末速度 m/s m/s 第二阶段重心下降的高度 = = m m 第三、四阶段交界时刻的速度  m/s m/s  m/s m/s 从而可计算出在第三阶段中身体重心上升的加速度 
设地面对该同学的支持力为 ,由牛顿第二定律有 ,由牛顿第二定律有 解得  N N N N 由牛顿第二定律知,该同学蹬地的作用力的大小 N N 【答案】(1) N (2) N (2) N N
| 
 A.a与b之间的压力减少,且a相对b向下滑动
A.a与b之间的压力减少,且a相对b向下滑动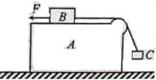 的绳是水平的。用一水平向左的拉力F作用在物体B上,恰使物体A、B、C保持相对静止,如图2所示,已知物体A、B、C、的质量均为m,重力加速度为g,不计所有的摩擦,则拉力F应为多大?
的绳是水平的。用一水平向左的拉力F作用在物体B上,恰使物体A、B、C保持相对静止,如图2所示,已知物体A、B、C、的质量均为m,重力加速度为g,不计所有的摩擦,则拉力F应为多大?
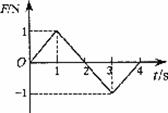 4.(2008年天津卷.理综.20)一个静止的质点,在0~4s时间内受到力F的作用,力的方向始终在同一直线上,力F随时间t的变化如图3所示,则质点在(
)
4.(2008年天津卷.理综.20)一个静止的质点,在0~4s时间内受到力F的作用,力的方向始终在同一直线上,力F随时间t的变化如图3所示,则质点在(
)
 A.箱内物体对箱子底部始终没有压力
A.箱内物体对箱子底部始终没有压力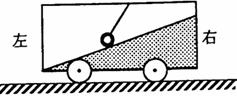 A.若小车向左运动,N可能为零
A.若小车向左运动,N可能为零
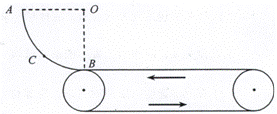 9.(2008年江苏学业水平测试卷.物理.27)如图7所示,固定的光滑圆弧轨道
9.(2008年江苏学业水平测试卷.物理.27)如图7所示,固定的光滑圆弧轨道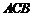 的半径为
的半径为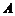 点与圆心
点与圆心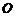 在同一水平线上, 圆弧轨道底端
在同一水平线上, 圆弧轨道底端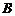 点与圆心在同一竖直线上.
点与圆心在同一竖直线上. 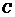 点离
点离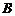 点的竖直高度为
点的竖直高度为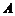 点由静止释放,滑过
点由静止释放,滑过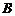 点后进入足够长的水平传送带,传送带由电动机驱动按图示方向运转,不计物块通过轨道与传送带交接处的动能损失,物块与传送带间的动摩擦因数为0.1,
点后进入足够长的水平传送带,传送带由电动机驱动按图示方向运转,不计物块通过轨道与传送带交接处的动能损失,物块与传送带间的动摩擦因数为0.1,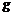 取
取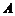 点下滑到
点下滑到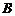 点时速度的大小。
图7
点时速度的大小。
图7 点下滑到传送带上后,又恰能返回到
点下滑到传送带上后,又恰能返回到 点,求物块在传送带上第一次往返所用的时间.
点,求物块在传送带上第一次往返所用的时间. 。直升机取水后飞往火场,加速度沿水平方向,大小稳定在a=
。直升机取水后飞往火场,加速度沿水平方向,大小稳定在a=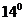 。如果空气阻力大小不变,且忽略悬索的质量,谋求水箱中水的质量M。(取重力加速度g=
。如果空气阻力大小不变,且忽略悬索的质量,谋求水箱中水的质量M。(取重力加速度g=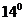 =0.242;cos
=0.242;cos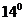 =0.970)
图8
=0.970)
图8  三、名校试题
三、名校试题 1.(2008年9月广东佛山禅城实验高中高级中学高三第一次月考试卷.物理.17)如图9所示,平板车长为L=
1.(2008年9月广东佛山禅城实验高中高级中学高三第一次月考试卷.物理.17)如图9所示,平板车长为L=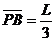 ,经过一段时间,小球脱离平板车落到地面.车与地面的动摩擦因数为0.2,其他摩擦均不计.取g=
,经过一段时间,小球脱离平板车落到地面.车与地面的动摩擦因数为0.2,其他摩擦均不计.取g=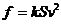 (其中k为比例系数).雨点接近地面时近似看做匀速直线运动,重力加速度为g.若把雨点看做球形,其半径为r,球的体积为
(其中k为比例系数).雨点接近地面时近似看做匀速直线运动,重力加速度为g.若把雨点看做球形,其半径为r,球的体积为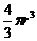 ,设雨点的密度为
,设雨点的密度为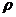 ,求:
,求: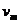 (用
(用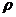 、r、g、k表示);
、r、g、k表示);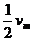 时,雨点的加速度a为多大?
时,雨点的加速度a为多大?
 3.(2009届湖南郴州高中毕业生调研题.物理。17)在农村人们盖房打地基叫打夯,夯锤的结构如图10所示,打夯共有5人,四个人分别握住夯锤的一个把手,一个人负责喊号,喊号人一声号子,四个人同时向上用力将夯锤提起,号音一落四人同时松手,夯锤落至地面将地基砸实。某次打夯时,设夯锤的质量为
3.(2009届湖南郴州高中毕业生调研题.物理。17)在农村人们盖房打地基叫打夯,夯锤的结构如图10所示,打夯共有5人,四个人分别握住夯锤的一个把手,一个人负责喊号,喊号人一声号子,四个人同时向上用力将夯锤提起,号音一落四人同时松手,夯锤落至地面将地基砸实。某次打夯时,设夯锤的质量为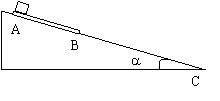 4.(安徽合肥一中2009届高三教学质量检测.物理.18)如图11所示,
4.(安徽合肥一中2009届高三教学质量检测.物理.18)如图11所示,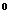 =0.6 cos37
=0.6 cos37 =
= )
) 5.(山东省潍坊市普通高中2009届高三上学期阶段性评估卷.物理.16)如图12所示,一滑块以
5.(山东省潍坊市普通高中2009届高三上学期阶段性评估卷.物理.16)如图12所示,一滑块以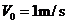 的速度从A点开始进入轨道ABC.已知AB段斜面倾角为53°,BC段斜面倾角为37°,
的速度从A点开始进入轨道ABC.已知AB段斜面倾角为53°,BC段斜面倾角为37°, 滑块与AB斜面的动摩擦因数为
滑块与AB斜面的动摩擦因数为 ,滑块与BC段动摩擦因数为
,滑块与BC段动摩擦因数为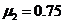 ,A点离B点所在水平面的高度
,A点离B点所在水平面的高度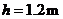 ,滑块运动中始终未脱离轨道,不计在B点的机械能损失,最大静摩擦力等于滑动摩擦力(取
,滑块运动中始终未脱离轨道,不计在B点的机械能损失,最大静摩擦力等于滑动摩擦力(取 ,
,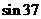 °=0.6,
°=0.6, °=0.8)求:
图12
°=0.8)求:
图12