|
试题详情
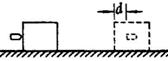 12.如图26所示,质量m的子弹以v0初速度水平射入放在光滑水平面上质量M的木块.子弹射入木块d深度后便随木块一起运动,试求木块对子弹平均阻力的大小.
图26 12.如图26所示,质量m的子弹以v0初速度水平射入放在光滑水平面上质量M的木块.子弹射入木块d深度后便随木块一起运动,试求木块对子弹平均阻力的大小.
图26
试题详情
试题详情
14.气功碎石表演中,质量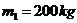 的石板压在演员身上,另一个演员举起质量 的石板压在演员身上,另一个演员举起质量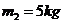 的铁锤,使劲地向石板咂去的瞬间,石板被砸碎了,而演员安然无恙,试通过分析和必要的理论计算来说明其中的奥妙。 的铁锤,使劲地向石板咂去的瞬间,石板被砸碎了,而演员安然无恙,试通过分析和必要的理论计算来说明其中的奥妙。 试题详情
试题详情
15.在小河上有一座小木桥,一演员携带两个演出用的铁球,其总重力正好略大于桥的最大负荷量,为了能一次完成过桥,有人提出让演员象演出一样将两球抛起并保证任何时刻至多只有一个小球在手中,这样一边抛球一边过河,如图28所示,问他这样能否安全过去?
图28
试题详情
16. 自动称米机已被许多大粮店广泛使用.买者认为:因为米流落到容器中时有向下的冲力不划算;卖者则认为:当预定米的质量数满足时,自动装置即刻切断米流时,此刻尚有一些米仍在空中,这些米间多给买者的,因而双方争执起来,究竟哪方说得对而划算呢?(原理如图29)
试题详情

图29 试题详情
 17.在纳米技术中需要移动或修补原子,必须使在不停地做热运动(速率约为几百米每秒)的原子几乎静止下来且能在一个小的空间区域内停留一段时间,为此发明了“激光致冷”技术。若把原子和入射光子分别类比为一辆小车和一个小球,则“激光致冷”与下述力学模型很类似:一辆质量为m的小车(一侧固定一轻弹簧),以如图27所示速度v0水平向右运动,一个动量大小为p,质量可以忽略的小球水平向左射入小车并压缩弹簧至最短,接着被锁定一段时间△T,再解除锁定后使小球以大小相同的动量p水平向右弹出,紧接着不断重复上述过程,最终小车停下来。设地面和车厢均光滑,除锁定时间△T外,不计小球在小车上运动和弹簧压缩、伸长时间,求: 17.在纳米技术中需要移动或修补原子,必须使在不停地做热运动(速率约为几百米每秒)的原子几乎静止下来且能在一个小的空间区域内停留一段时间,为此发明了“激光致冷”技术。若把原子和入射光子分别类比为一辆小车和一个小球,则“激光致冷”与下述力学模型很类似:一辆质量为m的小车(一侧固定一轻弹簧),以如图27所示速度v0水平向右运动,一个动量大小为p,质量可以忽略的小球水平向左射入小车并压缩弹簧至最短,接着被锁定一段时间△T,再解除锁定后使小球以大小相同的动量p水平向右弹出,紧接着不断重复上述过程,最终小车停下来。设地面和车厢均光滑,除锁定时间△T外,不计小球在小车上运动和弹簧压缩、伸长时间,求:
(1)小球第一次入射后再弹出时,小车速度大小和这一过程 中小车动能的减少量;
(2)从小球第一次入射开始到小车停止运动所经历的时间。 试题详情
高考真题 1.【解析】设物体的质量为m,t0时刻受盒子碰撞获得速度v,根据动量守恒定律  3t0时刻物体与盒子右壁碰撞使盒子速度又变为v0,说明碰撞是弹性碰撞   联立以上两式解得 m=M 联立以上两式解得 m=M
(也可通过图象分析得出v0=v,结合动量守恒,得出正确结果) 【答案】m=M 2.【解析】由动量守恒定律和能量守恒定律得:  
解得: 炮弹射出后做平抛,有:  解得目标A距炮口的水平距离为: 同理,目标B距炮口的水平距离为:

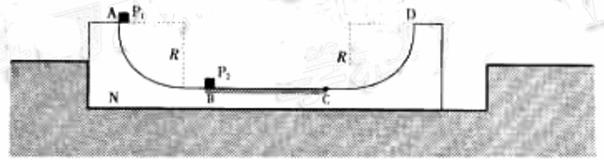
解得: 【答案】 3.【解析】(1)P1滑到最低点速度为 ,由机械能守恒定律有: ,由机械能守恒定律有:  解得: 解得:
P1、P2碰撞,满足动量守恒,机械能守恒定律,设碰后速度分别为 、 、  
解得:  =5m/s =5m/s P2向右滑动时,假设P1保持不动,对P2有: (向左) (向左) 对P1、M有:  此时对P1有: ,所以假设成立。 ,所以假设成立。 (2)P2滑到C点速度为 ,由 ,由 得 得 P1、P2碰撞到P2滑到C点时,设P1、M速度为v,对动量守恒定律:  解得: 解得:
对P1、P2、M为系统: 代入数值得: 滑板碰后,P1向右滑行距离: P2向左滑行距离: 所以P1、P2静止后距离: 【答案】(1) (2) (2) 4.【解析】(1)P1经t1时间与P2碰撞,则
P1、P2碰撞,设碰后P2速度为v2,由动量守恒: 解得 (水平向左) (水平向左)  (水平向右) (水平向右) 碰撞后小球P1向左运动的最大距离: 又:
又: 解得: 所需时间: (2)设P1、P2碰撞后又经 时间在OB区间内再次发生碰撞,且P1受电场力不变,由运动学公式,以水平向右为正: 时间在OB区间内再次发生碰撞,且P1受电场力不变,由运动学公式,以水平向右为正: 则: 则: 解得: (故P1受电场力不变) (故P1受电场力不变) 对P2分析:  所以假设成立,两球能在OB区间内再次发生碰撞。 5.【解析】从两小球碰撞后到它们再次相遇,小球A和B的速度大小保持不变。根据它们通过的路程,可知小球B和小球A在碰撞后的速度大小之比为4┱1。 设碰撞后小球A和B 的速度分别为 和 和 ,在碰撞过程中动量守恒,碰撞前后动能相等,有 ,在碰撞过程中动量守恒,碰撞前后动能相等,有  ………… ① ………… ①  ………… ② ………… ② 联立以上两式再由 ,可解出 m1∶m2=2∶1 ,可解出 m1∶m2=2∶1 【答案】2∶1 6.【解析】⑴碰后B上摆过程机械能守恒,可得 。 。 ⑵两球发生弹性碰撞过程系统动量守恒,机械能守恒。设与B碰前瞬间A的速度是v0,有2mv0=2mvA+mvB, ,可得vA= v0/3,vB=
4v0/3,因此 ,可得vA= v0/3,vB=
4v0/3,因此 ,同时也得到 ,同时也得到 。 。 ⑶先由A平抛的初速度vA和水平位移L/2,求得下落高度恰好是L。即两球碰撞点到水平面的高度是L。A离开弹簧时的初动能可以认为就等于弹性力对A做的功。A离开弹簧上升的全过程用机械能守恒: ,解得W= ,解得W=  【答案】(1) (2)W= (2)W=  7.【解析】此题是单个质点碰撞的多过程问题,既可以用动能定理与动量定理求解,也可以用力与运动关系与动量求解.设小物块从高为h处由静止开始沿斜面向下运动,到达斜面底端时速度为v。
由动能定理得 ①
① 以沿斜面向上为动量的正方向。按动量定理,碰撞过程中挡板给小物块的冲量  ② ②
设碰撞后小物块所能达到的最大高度为h’,则 ③ ③
同理,有  ④ ④  ⑤ ⑤
式中,v’为小物块再次到达斜面底端时的速度,I’为再次碰撞过程中挡板给小物块的冲量。由①②③④⑤式得 ⑥式中 ⑥式中  ⑦ ⑦
由此可知,小物块前4次与挡板碰撞所获得的冲量成等比级数,首项为  ⑧总冲量为 ⑧总冲量为  ⑨ ⑨ 由 (  ⑩得 ⑩得 ⑾ ⑾ 代入数据得  N?s N?s
【答案】  N?s N?s 8.【解析】此题开始的绳连的系统,后粘合变成了小球单个质点的运动问题(1)对系统,设小球在最低点时速度大小为v1,此时滑块的速度大小为v2,滑块与挡板接触前由系统的机械能守恒定律:mgl = mv12 +mv22① 由系统的水平方向动量守恒定律:mv1 = mv2② 对滑块与挡板接触到速度刚好变为零的过程中,挡板阻力对滑块的冲量为:I =
mv2③ 联立①②③解得I = m 方向向左④ (2)小球释放到第一次到达最低点的过程中,设绳的拉力对小球做功的大小为W,对小球由动能定理:mgl+W = mv12⑤ 联立①②⑤解得:W =-mgl,即绳的拉力对小球做负功,大小为mgl 。 【答案】(1)I = m 方向向左;(2)mgl 9.【解析】(1)设B在绳被拉断后瞬间的速度为 ,到达C点时的速度为 ,到达C点时的速度为 ,有 ,有  (1) (1) (2) (2)
代入数据得 (3)
(3) (2)设弹簧恢复到自然长度时B的速度为 ,取水平向右为正方向,有 ,取水平向右为正方向,有  (4) (4) (5)
(5)
代入数据得  其大小为4NS (6) 其大小为4NS (6) (3)设绳断后A的速度为 ,取水平向右为正方向,有 ,取水平向右为正方向,有  (7) (7) 代入数据得 代入数据得
【答案】(1) (2)4NS (3) (2)4NS (3) 10.【解析】设摆球A、B的质量分别为 、 、 ,摆长为l,B球的初始高度为h1,碰撞前B球的速度为vB.在不考虑摆线质量的情况下,根据题意及机械能守恒定律得 ,摆长为l,B球的初始高度为h1,碰撞前B球的速度为vB.在不考虑摆线质量的情况下,根据题意及机械能守恒定律得  ①
①
 ②
②
设碰撞前、后两摆球的总动量的大小分别为P1、P2。有 P1=mBvB ③ 联立①②③式得  ④
④
同理可得  ⑤
⑤
联立④⑤式得
代入已知条件得 由此可以推出
由此可以推出 ≤4% ≤4%
所以,此实验在规定的范围内验证了动量守恒定律。 【答案】 ≤4% ≤4% 名校试题 1.【解析】(1)M静止时,设弹簧压缩量为l0,则Mg=kl0 ① 速度最大时,M、m组成的系统加速度为零,则 (M+m)g-k(l0+l1)=0 ②- 联立①②解得:k=50N/m ③
[或:因M初位置和速度最大时都是平衡状态,故mg=kl1,解得:k=50N/m] (2)m下落h过程中,mgh= mv02 ④- mv02 ④- m冲击M过程中, m v0=(M+m)v ⑤- 所求过程的弹性势能的增加量:ΔE=(M+m)g(l1+l2)+ (M+m)v2 ⑥ (M+m)v2 ⑥ 联立④⑤⑥解得:ΔE=0.66J ⑦ (用弹性势能公式计算的结果为ΔE=0.65J也算正确) 【答案】ΔE=0.66J 2.【解析】①根据图象可知,物体C与物体A相碰前的速度为:v1=6m/s 相碰后的速度为:v2=2m/s 根据定量守恒定律得: … … 解得:m3=2.0kg ②规定向左的方向为正方向,在第5.0s和第15s末物块A的速度分别为: v2=2m/s,v3=-2m/s 所以物块A的动量变化为: 即在5.0s到15s的时间内物块A动量变化的大小为:16kg?m/s 方向向右 【答案】(1)m3=2.0kg
(2)16kg?m/s 方向向右 3.【解析】(1)设第一颗子弹进入靶盒A后,子弹与靶盒的共内速度为 。 。 根据碰撞过程系统动量守恒,有: 设A离开O点的最大距离为 ,由动能定理有: ,由动能定理有: 解得: (2)根据题意,A在的恒力F的作用返回O点时第二颗子弹正好打入,由于A的动量与第二颗子弹动量大小相同,方向相反,故第二颗子弹打入后,A将静止在O点。设第三颗子弹打入A后,它们的共同速度为 ,由系统动量守恒得: ,由系统动量守恒得: (2分) (2分) 设A从离开O点到又回到O点所经历的时间为t,取碰后A运动的方向为正方向,由动量定理得: 解得: 解得: (3)从第(2)问的计算可以看出,第1、3、5、……(2n+1)颗子弹打入A后,A运动时间均为 故总时间 故总时间 【答案】(1) (2) (2) (3) (3) 4.【解析】对A、B、C整体,从C以v0滑上木块到最终B、C达到共同速度V, 其动量守恒既:m v0=2mV1+3mv 1.8=2V1+3×0.4 V1=0.3m/s
对A、B、C整体,从C以v0滑上木块到C以V2刚离开长木板, 此时A、B具有共同的速度V1。其动量守恒即:m v0=mV2+4mv1 1.8=V2+4×0.3 V2=0.6m/s 【答案】 (1)V1=0.3m/s (2)
V2=0.6m/s 5.【解析】(1)B与A碰撞前速度由动能定理 得  B与A碰撞,由动量守恒定律
得  碰后到物块A、B运动至速度减为零,弹簧的最大弹性势能  (2)设撤去F后,A、B一起回到O点时的速度为 ,由机械能守恒得 ,由机械能守恒得   返回至O点时,A、B开始分离,B在滑动摩擦力作用下向左作匀减速直线运动,设物块B最终离O点最大距离为x 由动能定理得:
 【答案】(1) (2) (2) 6.【解析】设小车初速度为V0,A与车相互作用摩擦力为f, 第一次碰后A与小车相对静止时速为 V1,由动量守恒, 得 mAV0-mBV0=(mA+mB)V1 由能量守恒,得 mAV02+ mAV02+ mBV02=f? mBV02=f? L+ L+ (mA+mB)V12… 图14 (mA+mB)V12… 图14 多次碰撞后,A停在车右端,系统初动能全部转化为内能,由能量守恒,得 fL= (mA+mB)V02… (mA+mB)V02… 联系以上三式,解得:(mA+mB)2=4(mA-mB)2  = = ∴mA=3mB ∴mA=3mB 【答案】mA=3mB 7.【解析】(1)当B离开墙壁时,A的速度为v0,由机械能守恒有
 mv02=E
解得 v0= mv02=E
解得 v0=
(2)以后运动中,当弹簧弹性势能最大时,弹簧达到最大程度时,A、B速度相等,设为v,由动量守恒有 2mv=mv0 解得
v=  (3)根据机械能守恒,最大弹性势能为
Ep= mv02- mv02- 2mv2= 2mv2= E E
【答案】(1)v0= (2)v= (2)v=  (3)Ep= (3)Ep= E E 8.【解析】设子弹的质量为m,木块的质量为M,子弹射出枪口时的速度为v0。 第一颗子弹射入木块时,动量守恒  木块带着子弹做平抛运动   第二颗子弹射入木块时,动量守恒  木块带着两颗子弹做平抛运动   联立以上各式解得  【答案】 9.【解析】

车与缓冲器短时相撞过程根据动量守恒:  ②
2分 ②
2分 O到D过程  ③ ③ 由①②③求得:
(2)D到O过程  ④ ④ 赛车从O点到停止运动  ⑤ ⑤
车整个过程克服摩擦力做功  ⑥ ⑥ 由④⑤⑥求得: 【答案】(1)  (2) (2)  10.【解析】(1)设所有物块都相对木板静止时的速度为 v ,因木板与所有物块系统水平方向不受外力,动量守恒,应有: ,因木板与所有物块系统水平方向不受外力,动量守恒,应有: m v +m?2 v +m?2 v +m?3 v +m?3 v +…+m?n v +…+m?n v =(M + nm)v =(M + nm)v 1 1
M = nm,
2 解得:
v = = (n+1)v (n+1)v ,
6分 ,
6分 (2)设第1号物块相对木板静止时的速度为v ,取木板与物块1为系统一部分,第2 号物块到第n号物块为系统另一部分,则 ,取木板与物块1为系统一部分,第2 号物块到第n号物块为系统另一部分,则 木板和物块1 △p =(M + m)v - m v - m v , , 2至n号物块 △p =(n-1)m?(v =(n-1)m?(v - v - v ) ) 由动量守恒定律: △p=△p , , 解得
v = = v v ,
3
6分 ,
3
6分 (3)设第k号物块相对木板静止时的速度由v ,则第k号物块速度由k v ,则第k号物块速度由k v 减为v 减为v 的过程中,序数在第k号物块后面的所有物块动量都减小m(k
v 的过程中,序数在第k号物块后面的所有物块动量都减小m(k
v - v - v ),取木板与序号为1至K号以前的各物块为一部分,则 ),取木板与序号为1至K号以前的各物块为一部分,则 △p=(M+km)v -(m v -(m v +m?2 v +m?2 v +…+mk v +…+mk v )=(n+k)m v )=(n+k)m v - - (k+1)m v (k+1)m v 序号在第k以后的所有物块动量减少的总量为 △p =(n-k)m(k v =(n-k)m(k v - v - v ) ) 由动量守恒得 △p=△p ,
即 ,
即 (n+k)m v - - (k+1)m v (k+1)m v = (n-k)m(k v = (n-k)m(k v - v - v ), ), 解得 v = = 【答案】 11.【解析】(1)设地球质量为M0,在地球表面,有一质量为m的物体, 设空间站质量为m′绕地球作匀速圆周运动时, 联立解得, (2)因为探测器对喷射气体做功的功率恒为P,而单位时间内喷气质量为m,故在t时 间内,据动能定理可求得喷出气体的速度为: 另一方面探测器喷气过程中系统动量守恒,则: 又探测器的动能, 联立解得: 【答案】(1)  (2) (2)  考点预测题 1.【解析】把A、B看成一个系统,弹簧弹力为内力,系统所受外力之和为零,故适用动量守恒定律,在烧断细绳前系统总动量为零,烧断细绳后,A、B的动量和也应为零. 0=PA’-PB’ PA’= PB’ 再根据 ,可得: ,可得:

【答案】 2.【解析】因为冲理是矢量,两个力的冲量相同要大小相等,方向相同;现时力对物体做的功,主要看力和在力方向上的位移。所以选项D正确 【答案】D 3.【解析】设地面对运动员的作用力为F,则由动量定理得:(F-mg)Δt=FΔt=mv+mgΔt;运动员从下蹲状态到身体刚好伸直离开地面,地面对运动员做功为零,这是因为地面对人的作用力沿力的方向没有位移.所以正确答案是B 【答案】B 4.【解析】此题是连续介质的冲击作用的问题,不少考生对这题感到无从下手。解答的关键是选Δm作为研究对象(即所谓微元法),再运用动量定理列式。以1秒内下落的雨滴为研究对象,设圆柱形水杯的底成积为S,其质量为 ,根据动量定理 ,根据动量定理 ,而 ,而 ,所以P= ,所以P= ,故选项A正确。 ,故选项A正确。 【答案】A 5. 【解析】篮球从h1处下落的时间为t1,触地时速度大小为v1,弹起时速度大小为v2. 则 ①
①
 ② ②
球弹起的速度大小 ③
③
球与地面作用时间 ④ ④ 球触地过程中取向上为正方向,根据动量定理有:  ⑤
⑤
即  ,代入数据得 ,代入数据得 . . 根据牛顿第三定律,球对地面的平均作用力方向竖直向下,大小为39N. 【答案】大小为39N. 6.【解析】此题既可以用整体法求解,也可以用隔离法求解 方法1:隔离法,先 以a和船(包括b)为系统,取 为正方向,设a向前跳入水中后,船速为 为正方向,设a向前跳入水中后,船速为 ,有: ,有:  ① ① 再以b和船为系统,设b向后跳入水中后船速为 ,则 ,则
 ② ② 解①②得, ,方向与 ,方向与 一致。 一致。 方法2:整体法,以a、b和船整体为研究系统,选择全过程为研究过程,有  也解得 也解得 【答案】 7.【解析】此题由研究对象的不同选取,所以解法也多种多样 方法1:隔离法,取其中的部分的物体用动量守恒,令 为正方向, 为正方向, 以小船和大船投过的麻袋为系统  ① ① 以大船和小船投过的麻袋为系统  ② ② 解①②得,  1 m/s 1 m/s  9 m/s 9 m/s 方法2:整体法与隔离法,对所有船和麻袋整体,全过程用动量守恒  ③
③ 联立③和①②式中的任意一个可得同样结果 【答案】 1 m/s 1 m/s  9 m/s 9 m/s 8.【解析】由自由落体的规律得 ……① ……① 由于球与地之间发生弹性碰撞,所以小球原速反弹,球再与木棍发生碰撞,取竖直向上为动量的正方向,根据动量守恒定律得m1v1-m2v1=m2v2……② B作竖直上抛运动m2v22/2=m2gh……③ 整理得h=(m1-m2)2H/m22……④
代入数据得h=4.05m>1.25m
图19 【答案】h=4.05m 9.【解析】设 为A从离开桌面至落 为A从离开桌面至落
| | | 

 倍,P1的质量为m1,带电量为q,P2的质量m2=
倍,P1的质量为m1,带电量为q,P2的质量m2=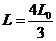 .已知
.已知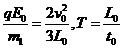 .
.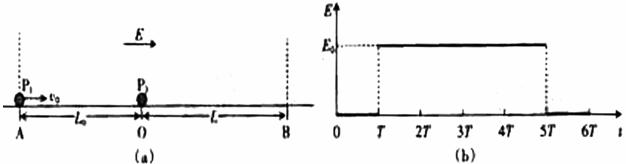
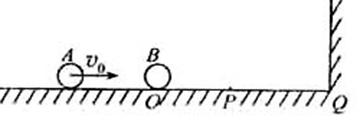
 5.(2007年宁夏卷.理综.30D)在光滑的水平面上,质量为m1的小球A以速率v0向右运动,在小球A的前方O点有一质量为m2的小球B处于静止状态,如图5所示。小球A与小球B发生正碰后小球A、B均向右运动,
5.(2007年宁夏卷.理综.30D)在光滑的水平面上,质量为m1的小球A以速率v0向右运动,在小球A的前方O点有一质量为m2的小球B处于静止状态,如图5所示。小球A与小球B发生正碰后小球A、B均向右运动,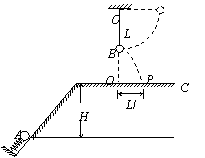
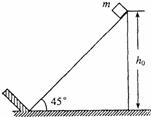 7.(2008年四川卷.理综.24)一倾角为θ=45°的斜面固定于地面,斜面顶端离地面的高度h0=
7.(2008年四川卷.理综.24)一倾角为θ=45°的斜面固定于地面,斜面顶端离地面的高度h0=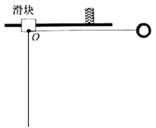 8.(2008年全国卷.理综.24)图8中滑块和小球的质量均为m,滑块可在水平放置的光滑固定导轨上自由滑动,小球与滑块上的悬点O由一不可伸长的轻绳相连,轻绳长为l。开始时,轻绳处于水平拉直状态,小球和滑块均静止。现将小球由静止释放,当小球到达最低点时,滑块刚好被一表面涂有粘性物质的固定挡板粘住,在极短的时间内速度减为零,小球继续向左摆动,当轻绳与竖直方向的夹角θ=60°时小球达到最高点。求
8.(2008年全国卷.理综.24)图8中滑块和小球的质量均为m,滑块可在水平放置的光滑固定导轨上自由滑动,小球与滑块上的悬点O由一不可伸长的轻绳相连,轻绳长为l。开始时,轻绳处于水平拉直状态,小球和滑块均静止。现将小球由静止释放,当小球到达最低点时,滑块刚好被一表面涂有粘性物质的固定挡板粘住,在极短的时间内速度减为零,小球继续向左摆动,当轻绳与竖直方向的夹角θ=60°时小球达到最高点。求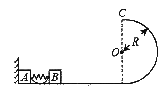 /s2,求
/s2,求
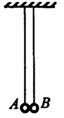 10.(2008年宁夏卷.物理.32②)某同学利用如图10所示的装置验证动量守恒定律。图中两摆摆长相同,悬挂于同一高度,A、B两摆球均很小,质量之比为1∶2。当两摆均处于自由静止状态时,其侧面刚好接触。向右上方拉动B球使其摆线伸直并与竖直方向成45°角,然后将其由静止释放。结果观察到两摆球粘在一起摆动,且最大摆角成30°。若本实验允许的最大误差为±4%,此实验是否成功地验证了动量守恒定律?
图10
10.(2008年宁夏卷.物理.32②)某同学利用如图10所示的装置验证动量守恒定律。图中两摆摆长相同,悬挂于同一高度,A、B两摆球均很小,质量之比为1∶2。当两摆均处于自由静止状态时,其侧面刚好接触。向右上方拉动B球使其摆线伸直并与竖直方向成45°角,然后将其由静止释放。结果观察到两摆球粘在一起摆动,且最大摆角成30°。若本实验允许的最大误差为±4%,此实验是否成功地验证了动量守恒定律?
图10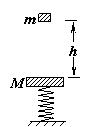 1.(
(广东省2009届新洲中学高三摸底考试试卷.物理.15)如图11所示,质量为M=
1.(
(广东省2009届新洲中学高三摸底考试试卷.物理.15)如图11所示,质量为M=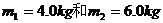 ,用轻弹簧相连结放在光滑的水平面上,物体B左侧与竖直墙相接触。另有一个物体C从t=0时刻起以一定的速度向左运动,在t=0.5s时刻与物体A相碰,碰后立即与A粘在一起不再分开。物体C的v ? t图象如图13所示。试求:
,用轻弹簧相连结放在光滑的水平面上,物体B左侧与竖直墙相接触。另有一个物体C从t=0时刻起以一定的速度向左运动,在t=0.5s时刻与物体A相碰,碰后立即与A粘在一起不再分开。物体C的v ? t图象如图13所示。试求: