精英家教网 >
试题搜索列表 >在(2)的条件下,当BCM的面积最大时,在抛物线的对称轴上存在点Q,使得△CNQ为直角三角
在(2)的条件下,当BCM的面积最大时,在抛物线的对称轴上存在点Q,使得△CNQ为直角三角答案解析
科目:czsx
来源:
题型:
如图1,抛物线y=x
2-4x+c交x轴于点A和B(-1,0)交y轴于点C,且抛物线的对称轴交x轴于点D
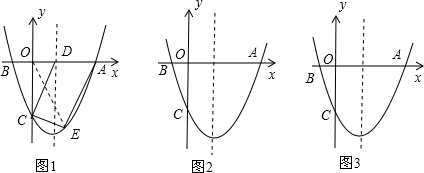
(1)求这个抛物线的解析式;
(2)若点E在抛物线上,且位于第四象限,当四边形ADCE面积最大时,求点E的坐标;
(3)如图2,在抛物线上是否存在这样的点P,使△PAB中的内角中有一边与x轴所夹锐角的正切值为
?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:

如图,矩形DEFG的边EF在△ABC的边BC上,顶点D、G分别在边AB、AC上,AH⊥BC,垂足为H.已知BC=12,AH=8.当矩形DEFG面积最大时,求矩形的长和宽.
查看答案和解析>>
科目:czsx
来源:
题型:
如图所示,矩形DEFG的边EF在△ABC的边BC上,顶点D、G分别在边AB、AC上,AH为BC边上的高,AH交DG于点P,已知AH=3,BC=5;
(1)设DG的长为x,矩形DEFG面积为y,求y关于x的函数解析式及其定义域;
(2)根据(1)中所得y关于x的函数图象,求当矩形DEFG面积最大时,DG的长为多少?矩形DEFG面积是多少?
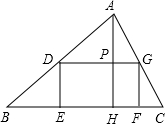
查看答案和解析>>
科目:czsx
来源:
题型:
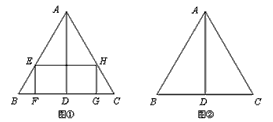
如图,已知等边三角形ABC的边长为2,AD是BC边上的高.
(1)在△ABC内部作一个矩形EFGH(如图①),其中E、H分别在边AB、AC上,FG在边BC上.
①设矩形的一边FG=x,那么EF=
;(用含有x的代数式表示)
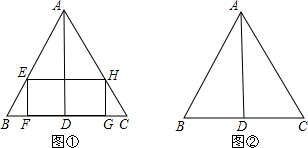
②设矩形的面积为y,当x取何值时,y的值最大,最大值是多少?
(2)当矩形EFGH面积最大时,请在图②中画出此时点E的位置.(要求尺规作图,保留作图痕迹,并简要说明确定点E的方法)
查看答案和解析>>
科目:czsx
来源:
题型:
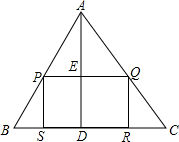
已知:如图所示,在△ABC中,BC=100,边BC上的高为50.在这个三角形内有一个内接矩形PQRS.
(1)若矩形的长PQ与宽PS的比是3:1,求这个矩形的长与宽;
(2)当这个矩形面积最大时,它的长与宽各是多少?
查看答案和解析>>
科目:czsx
来源:
题型:
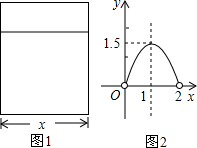
用铝合金型材做一个形状如图1所示的矩形窗框,设窗框的一边为x m.窗户的适光面积为ym
2,y与x的函数图象如图2所示.
(1)当窗户透光面积最大时,求窗框的两边长;
(2)要使窗户透光面积不小于1m
2.则窗框的一边长x应该在什么范围内取值?
查看答案和解析>>
科目:czsx
来源:
题型:
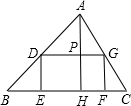
如图,有一块三角形土地,它的底边BC=100米,高AH=80米,某单位要沿着地边BC修一座底面是矩形DEFG的大楼,D、G分别在AB、AC的边上,问当这个矩形面积最大时,它的长与宽各是多少米?面积最大为多少平方米?
查看答案和解析>>
科目:czsx
来源:2009年重庆市南开中学中考数学一模试卷(解析版)
题型:解答题
如图1,抛物线y=x
2-4x+c交x轴于点A和B(-1,0)交y轴于点C,且抛物线的对称轴交x轴于点D

(1)求这个抛物线的解析式;
(2)若点E在抛物线上,且位于第四象限,当四边形ADCE面积最大时,求点E的坐标;
(3)如图2,在抛物线上是否存在这样的点P,使△PAB中的内角中有一边与x轴所夹锐角的正切值为

?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
如图,已知等边三角形ABC的边长为2,AD是BC边上的高.
⑴在△ABC内部作一个矩形EFGH(如图①),其中E、H分别在边AB、AC上,FG在边BC上.
① 设矩形的一边FG=x,那么EF= ▲ .(用含有x的代数式表示)
② 设矩形的面积为y,当x取何值时,y的值最大?最大值是多少?
⑵当矩形EFGH面积最大时,请在图②中画出此时点E的位置.(要求尺规作图,保留作图痕迹,并简要说明确定点E的方法)
查看答案和解析>>
科目:czsx
来源:2010-2011学年安徽省安庆市桐城二中九年级(上)第二次月考数学试卷(解析版)
题型:解答题
如图,有一块三角形土地,它的底边BC=100米,高AH=80米,某单位要沿着地边BC修一座底面是矩形DEFG的大楼,D、G分别在AB、AC的边上,问当这个矩形面积最大时,它的长与宽各是多少米?面积最大为多少平方米?

查看答案和解析>>
科目:czsx
来源:2009年上海市卢湾区中考数学一模试卷(解析版)
题型:解答题
(2009•卢湾区一模)如图所示,矩形DEFG的边EF在△ABC的边BC上,顶点D、G分别在边AB、AC上,AH为BC边上的高,AH交DG于点P,已知AH=3,BC=5;
(1)设DG的长为x,矩形DEFG面积为y,求y关于x的函数解析式及其定义域;
(2)根据(1)中所得y关于x的函数图象,求当矩形DEFG面积最大时,DG的长为多少?矩形DEFG面积是多少?

查看答案和解析>>
科目:czsx
来源:江苏省模拟题
题型:解答题
如图,已知等边三角形ABC的边长为2,AD是BC边上的高.
(1)在△ABC内部作一个矩形EFGH(如图①),其中E、H分别在边AB、AC上,FG在边BC上.
① 设矩形的一边FG=x,那么EF=( ).(用含有x的代数式表示)
② 设矩形的面积为y,当x取何值时,y的值最大?最大值是多少?
(2)当矩形EFGH面积最大时,请在图②中画出此时点E的位置.(要求尺规作图,保留作图痕迹,并简要说明确定点E的方法)
查看答案和解析>>
科目:czsx
来源:
题型:解答题
如图,已知等边三角形ABC的边长为2,AD是BC边上的高.
(1)在△ABC内部作一个矩形EFGH(如图①),其中E、H分别在边AB、AC上,FG在边BC上.
①设矩形的一边FG=x,那么EF=______;(用含有x的代数式表示)
②设矩形的面积为y,当x取何值时,y的值最大,最大值是多少?
(2)当矩形EFGH面积最大时,请在图②中画出此时点E的位置.(要求尺规作图,保留作图痕迹,并简要说明确定点E的方法)
查看答案和解析>>
科目:czsx
来源:
题型:解答题
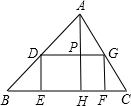 如图,有一块三角形土地,它的底边BC=100米,高AH=80米,某单位要沿着地边BC修一座底面是矩形DEFG的大楼,D、G分别在AB、AC的边上,问当这个矩形面积最大时,它的长与宽各是多少米?面积最大为多少平方米?
如图,有一块三角形土地,它的底边BC=100米,高AH=80米,某单位要沿着地边BC修一座底面是矩形DEFG的大楼,D、G分别在AB、AC的边上,问当这个矩形面积最大时,它的长与宽各是多少米?面积最大为多少平方米?
查看答案和解析>>
科目:czsx
来源:
题型:解答题
 用铝合金型材做一个形状如图1所示的矩形窗框,设窗框的一边为x m.窗户的适光面积为ym2,y与x的函数图象如图2所示.
用铝合金型材做一个形状如图1所示的矩形窗框,设窗框的一边为x m.窗户的适光面积为ym2,y与x的函数图象如图2所示.
(1)当窗户透光面积最大时,求窗框的两边长;
(2)要使窗户透光面积不小于1m2.则窗框的一边长x应该在什么范围内取值?
查看答案和解析>>
科目:czsx
来源:
题型:解答题
如图所示,矩形DEFG的边EF在△ABC的边BC上,顶点D、G分别在边AB、AC上,AH为BC边上的高,AH交DG于点P,已知AH=3,BC=5;
(1)设DG的长为x,矩形DEFG面积为y,求y关于x的函数解析式及其定义域;
(2)根据(1)中所得y关于x的函数图象,求当矩形DEFG面积最大时,DG的长为多少?矩形DEFG面积是多少?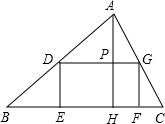
查看答案和解析>>
科目:czsx
来源:
题型:
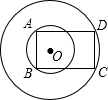
如图,两圆同心,半径分别为6与8,又矩形ABCD的边AB和CD分别为小大两圆的弦.则当矩形ABCD面积最大时,求此矩形的周长.
查看答案和解析>>
科目:czsx
来源:
题型:
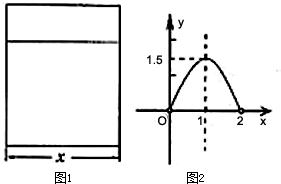
7、用铝合金型材做一个形状如图1所示的矩形窗框,设窗框的一边为xm,窗户的透光面积为ym
2,y与x的函数图象如图2所示.
(1)观察图象,当x为何值时,窗户透光面积最大?
(2)当窗户透光面积最大时,窗框的另一边长是多少?
查看答案和解析>>
科目:czsx
来源:101网校同步练习 初三数学 人教版(新课标2004年初审) 人教实验版
题型:022
用铝合金型材料做一个形状如图1所示的矩形窗框,设窗框的一边为x m,窗户的透光面积为ym2,y与x的函数图象如图2所示.

(1)观察图象,当x=________m时,窗户透光面积最大.
(2)当窗户透光面积最大时,窗框的另一边长是________m.
查看答案和解析>>
科目:czsx
来源:2011-2012学年沪科版九年级(上)期末复习数学试卷(二)(解析版)
题型:解答题
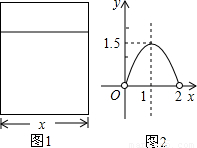
用铝合金型材做一个形状如图1所示的矩形窗框,设窗框的一边为xm,窗户的透光面积为ym
2,y与x的函数图象如图2所示.
(1)观察图象,当x为何值时,窗户透光面积最大?
(2)当窗户透光面积最大时,窗框的另一边长是多少?
查看答案和解析>>


 如图,矩形DEFG的边EF在△ABC的边BC上,顶点D、G分别在边AB、AC上,AH⊥BC,垂足为H.已知BC=12,AH=8.当矩形DEFG面积最大时,求矩形的长和宽.
如图,矩形DEFG的边EF在△ABC的边BC上,顶点D、G分别在边AB、AC上,AH⊥BC,垂足为H.已知BC=12,AH=8.当矩形DEFG面积最大时,求矩形的长和宽.
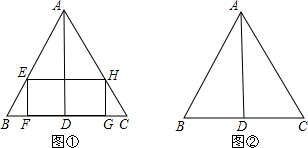
 已知:如图所示,在△ABC中,BC=100,边BC上的高为50.在这个三角形内有一个内接矩形PQRS.
已知:如图所示,在△ABC中,BC=100,边BC上的高为50.在这个三角形内有一个内接矩形PQRS. 用铝合金型材做一个形状如图1所示的矩形窗框,设窗框的一边为x m.窗户的适光面积为ym2,y与x的函数图象如图2所示.
用铝合金型材做一个形状如图1所示的矩形窗框,设窗框的一边为x m.窗户的适光面积为ym2,y与x的函数图象如图2所示. 如图,有一块三角形土地,它的底边BC=100米,高AH=80米,某单位要沿着地边BC修一座底面是矩形DEFG的大楼,D、G分别在AB、AC的边上,问当这个矩形面积最大时,它的长与宽各是多少米?面积最大为多少平方米?
如图,有一块三角形土地,它的底边BC=100米,高AH=80米,某单位要沿着地边BC修一座底面是矩形DEFG的大楼,D、G分别在AB、AC的边上,问当这个矩形面积最大时,它的长与宽各是多少米?面积最大为多少平方米? 
 ?若存在,求出点P的坐标;若不存在,请说明理由.
?若存在,求出点P的坐标;若不存在,请说明理由.



 如图,有一块三角形土地,它的底边BC=100米,高AH=80米,某单位要沿着地边BC修一座底面是矩形DEFG的大楼,D、G分别在AB、AC的边上,问当这个矩形面积最大时,它的长与宽各是多少米?面积最大为多少平方米?
如图,有一块三角形土地,它的底边BC=100米,高AH=80米,某单位要沿着地边BC修一座底面是矩形DEFG的大楼,D、G分别在AB、AC的边上,问当这个矩形面积最大时,它的长与宽各是多少米?面积最大为多少平方米? 用铝合金型材做一个形状如图1所示的矩形窗框,设窗框的一边为x m.窗户的适光面积为ym2,y与x的函数图象如图2所示.
用铝合金型材做一个形状如图1所示的矩形窗框,设窗框的一边为x m.窗户的适光面积为ym2,y与x的函数图象如图2所示.
 7、用铝合金型材做一个形状如图1所示的矩形窗框,设窗框的一边为xm,窗户的透光面积为ym2,y与x的函数图象如图2所示.
7、用铝合金型材做一个形状如图1所示的矩形窗框,设窗框的一边为xm,窗户的透光面积为ym2,y与x的函数图象如图2所示.
