科目:czsx
来源:
题型:

已知抛物线y=ax
2+bx+c的顶点坐标为P(-4,
-),与x轴交于A、B两点,与y轴交于点C,其中B点坐标为(1,0).
(1)求这条抛物线的函数解析式;
(2)若抛物线的对称轴交x轴于点D,则在线段AC上是否存在这样的点Q使得△ADQ为等腰三角形?若存在,请求出符合条件的点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
已知抛物线y=ax2+bx+c的顶点坐标为(4,-1),与y轴交于点C(0,3),O是原点.
(1)求这条抛物线的解析式;
(2)设此抛物线与x轴的交点为A,B(A在B的左边),问在y轴上是否存在点P,使以O,B,P为顶点的三角形与△AOC相似?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
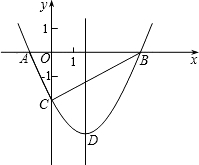
如图,抛物线y=
x
2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(-1,0).
(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,证明你的结论;
(3)点M(m,0)是x轴上的一个动点,当MC+MD的值最小时,求m的值.
[注:抛物线y=ax
2+bx+c的顶点坐标为(-
,
).].
查看答案和解析>>
科目:czsx
来源:
题型:
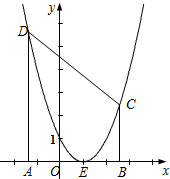
如图,已知抛物线y=ax
2+bx+c的顶点坐标为E(1,0),与y轴的交点坐标为(0,1).
(1)求该抛物线的函数关系式.
(2)A、B是x轴上两个动点,且A、B间的距离为AB=4,A在B的左边,过A作AD⊥x轴交抛物线于D,过B作BC⊥x轴交抛物线于C.设A点的坐标为(t,0),四边形ABCD的面积为S.
①求S与t之间的函数关系式.
②求四边形ABCD的最小面积,此时四边形ABCD是什么四边形?
③当四边形ABCD面积最小时,在对角线BD上是否存在这样的点P,使得△PAE的周长最小,若存在,请求出点P的坐标及这时△PAE的周长;若不存在,说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
如图所示,某同学在探究二次函数图象时,作直线y=m平行于x轴,交二次函数y=x
2的图象于A、B两点,作AC、BD分别垂直于x轴,发现四边形ABCD是正方形.
(1)求m的值及A、B两点的坐标;
(2)如图所示,将抛物线“y=x
2”改为“y=x
2-2x+2”,直线CD经过抛物线的顶点P与x轴平行,其它关系不变,求m的值及A、B两点的坐标.
(3)如图所示,将图中的改为“y=ax
2+bx+c(a>0),其它关系不变,请直接写出m的值及A、B两
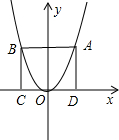
点的坐标(用含有a、b、c的代数式表示)
[提示:抛物线y=ax
2+bx+c的顶点坐标为(
-,
),对称轴为
x=-].
查看答案和解析>>
科目:czsx
来源:
题型:
如图,在直角坐标系中,矩形ABCD的边AD在y轴正半轴上,点A、C的坐标分别为(0,1)、(2,4).点P从点A出发,沿A⇒B⇒C以每秒1个单位的速度运动,到点C停止;点Q在x轴上,横坐标为点P的横、纵坐标之和.抛物线
y=-x2+bx+c经过A、C两点.过点P作x轴的垂线,垂足
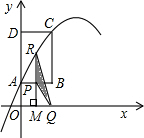
为M,交抛物线于点R.设点P的运动时间为t(秒),△PQR的面积为S(平方单位).
(1)求抛物线对应的函数关系式;
(2)分别求t=1和t=4时,点Q的坐标;
(3)当0<t≤5时,求S与t之间的函数关系式,并直接写出S的最大值.
参考公式:抛物线y=ax
2+bx+c的顶点坐标为
(-,
).
查看答案和解析>>
科目:czsx
来源:
题型:
已知抛物线y=ax
2+bx+c的顶点坐标为(2,4).
(Ⅰ)试用含a的代数式分别表示b,c;
(Ⅱ)若直线y=kx+4(k≠0)与y轴及该抛物线的交点依次为D、E、F,且
=,其中O为坐标原点,试用含a的代数式表示k;
(Ⅲ)在(Ⅱ)的条件下,若线段EF的长m满足3
≤m≤3
,试确定a的取值范围.
查看答案和解析>>
科目:czsx
来源:
题型:

如图,已知抛物线
y1=ax2+bx+c的顶点坐标为(2,1),且经过点B(
,),抛物线对称轴左侧与x轴交于点A,与y轴相交于点C.
(1)求抛物线解析式y
1和直线BC的解析式y
2;
(2)连接AB、AC,求△ABC的面积.
(3)根据图象直接写出y
1<y
2时自变量x的取值范围.
查看答案和解析>>
科目:czsx
来源:
题型:
抛物线y=ax2+bx+c的顶点坐标为(3,-2),与x轴两交点的距离为4,求抛物线的解析式.
查看答案和解析>>
科目:czsx
来源:2012年吉林省白城市镇赉县中考数学模拟试卷(二)(解析版)
题型:解答题
已知抛物线y=ax
2+bx+c的顶点坐标为P(-4,

),与x轴交于A、B两点,与y轴交于点C,其中B点坐标为(1,0).
(1)求这条抛物线的函数解析式;
(2)若抛物线的对称轴交x轴于点D,则在线段AC上是否存在这样的点Q使得△ADQ为等腰三角形?若存在,请求出符合条件的点Q的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:czsx
来源:2010年中考数学考前知识点回归+巩固 专题13 二次函数(解析版)
题型:解答题
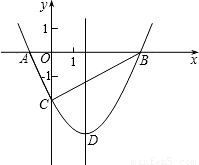
(2008•三明)如图,抛物线y=

x
2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(-1,0).
(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,证明你的结论;
(3)点M(m,0)是x轴上的一个动点,当MC+MD的值最小时,求m的值.
[注:抛物线y=ax
2+bx+c的顶点坐标为(-
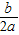
,
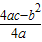
).].
查看答案和解析>>
科目:czsx
来源:第26章《二次函数》常考题集(21):26.3 实际问题与二次函数(解析版)
题型:解答题
如图,抛物线y=

x
2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(-1,0).
(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,证明你的结论;
(3)点M(m,0)是x轴上的一个动点,当MC+MD的值最小时,求m的值.
[注:抛物线y=ax
2+bx+c的顶点坐标为(-

,

).].

查看答案和解析>>
科目:czsx
来源:
题型:解答题
抛物线y=ax2+bx+c的顶点坐标为(3,-2),与x轴两交点的距离为4,求抛物线的解析式.
查看答案和解析>>
科目:czsx
来源:2009年海南省海口市国兴中学直升班数学考试试卷(解析版)
题型:解答题
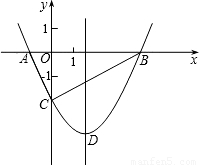
(2008•三明)如图,抛物线y=

x
2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(-1,0).
(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,证明你的结论;
(3)点M(m,0)是x轴上的一个动点,当MC+MD的值最小时,求m的值.
[注:抛物线y=ax
2+bx+c的顶点坐标为(-
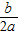
,
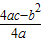
).].
查看答案和解析>>
科目:czsx
来源:第27章《二次函数》中考题集(37):27.3 实践与探索(解析版)
题型:解答题
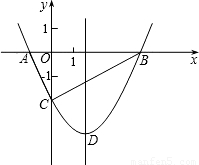
如图,抛物线y=

x
2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(-1,0).
(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,证明你的结论;
(3)点M(m,0)是x轴上的一个动点,当MC+MD的值最小时,求m的值.
[注:抛物线y=ax
2+bx+c的顶点坐标为(-

,

).].
查看答案和解析>>
科目:czsx
来源:2012年福建省漳州市龙文中学中考数学模拟试卷(解析版)
题型:解答题
如图,抛物线y=

x
2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(-1,0).
(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,证明你的结论;
(3)点M(m,0)是x轴上的一个动点,当MC+MD的值最小时,求m的值.
[注:抛物线y=ax
2+bx+c的顶点坐标为(-

,

).].

查看答案和解析>>
科目:czsx
来源:第2章《二次函数》常考题集(23):2.3 二次函数的应用(解析版)
题型:解答题
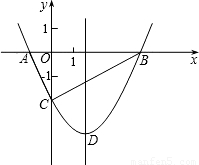
如图,抛物线y=

x
2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(-1,0).
(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,证明你的结论;
(3)点M(m,0)是x轴上的一个动点,当MC+MD的值最小时,求m的值.
[注:抛物线y=ax
2+bx+c的顶点坐标为(-

,

).].
查看答案和解析>>
科目:czsx
来源:第23章《二次函数与反比例函数》中考题集(41):23.5 二次函数的应用(解析版)
题型:解答题
已知抛物线y=ax
2+bx+c的顶点坐标为(2,4).
(Ⅰ)试用含a的代数式分别表示b,c;
(Ⅱ)若直线y=kx+4(k≠0)与y轴及该抛物线的交点依次为D、E、F,且
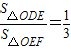
,其中O为坐标原点,试用含a的代数式表示k;
(Ⅲ)在(Ⅱ)的条件下,若线段EF的长m满足3

≤m≤3

,试确定a的取值范围.
查看答案和解析>>
科目:czsx
来源:2012年吉林省长春市中考数学模拟试卷(二)(解析版)
题型:解答题
如图,在直角坐标系中,矩形ABCD的边AD在y轴正半轴上,点A、C的坐标分别为(0,1)、(2,4).点P从点A出发,沿A⇒B⇒C以每秒1个单位的速度运动,到点C停止;点Q在x轴上,横坐标为点P的横、纵坐标之和.抛物线
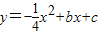
经过A、C两点.过点P作x轴的垂线,垂足为M,交抛物线于点R.设点P的运动时间为t(秒),△PQR的面积为S(平方单位).
(1)求抛物线对应的函数关系式;
(2)分别求t=1和t=4时,点Q的坐标;
(3)当0<t≤5时,求S与t之间的函数关系式,并直接写出S的最大值.
参考公式:抛物线y=ax
2+bx+c的顶点坐标为

,
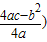
.

查看答案和解析>>
科目:czsx
来源:第2章《二次函数》中考题集(34):2.7 最大面积是多少(解析版)
题型:解答题
如图,抛物线y=

x
2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(-1,0).
(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,证明你的结论;
(3)点M(m,0)是x轴上的一个动点,当MC+MD的值最小时,求m的值.
[注:抛物线y=ax
2+bx+c的顶点坐标为(-

,

).].

查看答案和解析>>

 已知抛物线y=ax2+bx+c的顶点坐标为P(-4,-
已知抛物线y=ax2+bx+c的顶点坐标为P(-4,- 如图,抛物线y=
如图,抛物线y= 如图,已知抛物线y=ax2+bx+c的顶点坐标为E(1,0),与y轴的交点坐标为(0,1).
如图,已知抛物线y=ax2+bx+c的顶点坐标为E(1,0),与y轴的交点坐标为(0,1).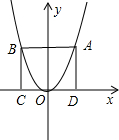 点的坐标(用含有a、b、c的代数式表示)
点的坐标(用含有a、b、c的代数式表示) 为M,交抛物线于点R.设点P的运动时间为t(秒),△PQR的面积为S(平方单位).
为M,交抛物线于点R.设点P的运动时间为t(秒),△PQR的面积为S(平方单位). 如图,已知抛物线y1=ax2+bx+c的顶点坐标为(2,1),且经过点B(
如图,已知抛物线y1=ax2+bx+c的顶点坐标为(2,1),且经过点B( ),与x轴交于A、B两点,与y轴交于点C,其中B点坐标为(1,0).
),与x轴交于A、B两点,与y轴交于点C,其中B点坐标为(1,0).
 x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(-1,0).
x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(-1,0).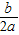 ,
,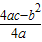 ).].
).].
 x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(-1,0).
x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(-1,0). ,
, ).].
).].
 x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(-1,0).
x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(-1,0).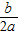 ,
,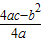 ).].
).].
 x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(-1,0).
x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(-1,0). ,
, ).].
).].
 x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(-1,0).
x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(-1,0). ,
, ).].
).].
 x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(-1,0).
x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(-1,0). ,
, ).].
).].
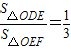 ,其中O为坐标原点,试用含a的代数式表示k;
,其中O为坐标原点,试用含a的代数式表示k; ≤m≤3
≤m≤3 ,试确定a的取值范围.
,试确定a的取值范围.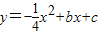 经过A、C两点.过点P作x轴的垂线,垂足为M,交抛物线于点R.设点P的运动时间为t(秒),△PQR的面积为S(平方单位).
经过A、C两点.过点P作x轴的垂线,垂足为M,交抛物线于点R.设点P的运动时间为t(秒),△PQR的面积为S(平方单位). ,
,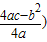 .
.
 x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(-1,0).
x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(-1,0). ,
, ).].
).].