
科目:czsx 来源: 题型:
科目:czsx 来源: 题型:
| 16 | 3 |
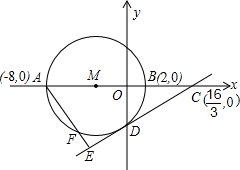 O为坐标原点.以AB为直径的⊙M与y轴的负半轴交于点D.
O为坐标原点.以AB为直径的⊙M与y轴的负半轴交于点D.科目:czsx 来源: 题型:
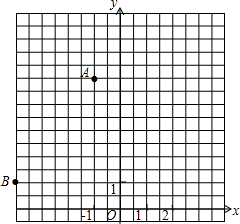 (2012•上虞市模拟)如图,已知平面直角坐标系中两点A(-1,5)、B(-4,1).
(2012•上虞市模拟)如图,已知平面直角坐标系中两点A(-1,5)、B(-4,1).科目:czsx 来源: 题型:
| 1 | 2 |
科目:czsx 来源:2005年全国中考数学试题汇编《图形的相似》(04)(解析版) 题型:解答题
 ,O为坐标原点.以AB为直径的⊙M与y轴的负半轴交于点D.
,O为坐标原点.以AB为直径的⊙M与y轴的负半轴交于点D.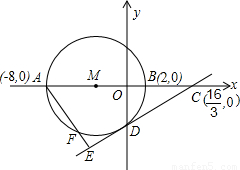
科目:czsx 来源:第3章《圆》中考题集(38):3.5 直线和圆的位置关系(解析版) 题型:解答题
 ,O为坐标原点.以AB为直径的⊙M与y轴的负半轴交于点D.
,O为坐标原点.以AB为直径的⊙M与y轴的负半轴交于点D.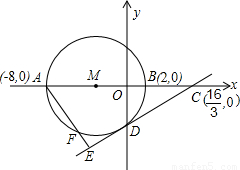
科目:czsx 来源:第27章《相似》中考题集(15):27.2 相似三角形(解析版) 题型:解答题
 ,O为坐标原点.以AB为直径的⊙M与y轴的负半轴交于点D.
,O为坐标原点.以AB为直径的⊙M与y轴的负半轴交于点D.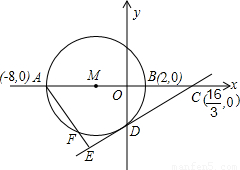
科目:czsx 来源:2007年初中毕业升学考试(山东潍坊卷)数学(带解析) 题型:解答题
如图,已知平面直角坐标系 中,点
中,点 ,
,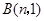 为两动点,其中
为两动点,其中 ,连结
,连结 ,
, .
.
(1)求证: ;
;
(2)当 时,抛物线经过
时,抛物线经过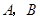 两点且以
两点且以 轴为对称轴,求抛物线对应的二次函数的关系式;
轴为对称轴,求抛物线对应的二次函数的关系式;
(3)在(2)的条件下,设直线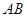 交
交 轴于点
轴于点 ,过点
,过点 作直线
作直线 交抛物线于
交抛物线于 两点,问是否存在直线
两点,问是否存在直线 ,使
,使 ?若存在,求出直线
?若存在,求出直线 对应的函数关系式;若不存在,请说明理由.
对应的函数关系式;若不存在,请说明理由.
科目:czsx 来源:2005年河南省中原油田中考数学试卷(大纲卷)(解析版) 题型:解答题
 ,O为坐标原点.以AB为直径的⊙M与y轴的负半轴交于点D.
,O为坐标原点.以AB为直径的⊙M与y轴的负半轴交于点D.
科目:czsx 来源:第35章《圆(二)》中考题集(21):35.4 切线的判定(解析版) 题型:解答题
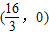 ,O为坐标原点.以AB为直径的⊙M与y轴的负半轴交于点D.
,O为坐标原点.以AB为直径的⊙M与y轴的负半轴交于点D.
科目:czsx 来源:2012届四川内江二中第二次中考模拟数学试卷(带解析) 题型:解答题
如图,已知平面直角坐标系 中,点A(2,m),B(-3,n)为两动点,其中m﹥1,连结
中,点A(2,m),B(-3,n)为两动点,其中m﹥1,连结 ,
, ,作
,作 轴于
轴于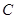 点,
点,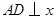 轴于
轴于 点.
点.
【小题1】求证:mn=6
【小题2】当 时,抛物线经过
时,抛物线经过 两点且以
两点且以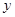 轴为对称轴,求抛物线对应的二次函数的关系式
轴为对称轴,求抛物线对应的二次函数的关系式
【小题3】在(2)的条件下,设直线 交
交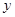 轴于点
轴于点 ,过点
,过点 作直线
作直线 交抛物线于
交抛物线于 两点,问是否存在直线
两点,问是否存在直线 ,使S⊿POF:S⊿QOF=1:2?若存在,求出直线
,使S⊿POF:S⊿QOF=1:2?若存在,求出直线 对应的函数关系式;若不存在,请说明理由.
对应的函数关系式;若不存在,请说明理由.
科目:czsx 来源:2005年全国中考数学试题汇编《三角形》(08)(解析版) 题型:解答题
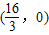 ,O为坐标原点.以AB为直径的⊙M与y轴的负半轴交于点D.
,O为坐标原点.以AB为直径的⊙M与y轴的负半轴交于点D.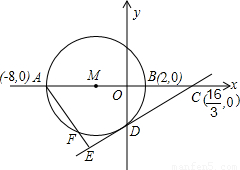
科目:czsx 来源:2007年初中毕业升学考试(山东潍坊卷)数学(解析版) 题型:解答题
如图,已知平面直角坐标系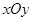 中,点
中,点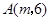 ,
,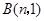 为两动点,其中
为两动点,其中 ,连结
,连结 ,
, .
.
(1)求证: ;
;
(2)当 时,抛物线经过
时,抛物线经过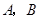 两点且以
两点且以 轴为对称轴,求抛物线对应的二次函数的关系式;
轴为对称轴,求抛物线对应的二次函数的关系式;
(3)在(2)的条件下,设直线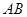 交
交 轴于点
轴于点 ,过点
,过点 作直线
作直线 交抛物线于
交抛物线于 两点,问是否存在直线
两点,问是否存在直线 ,使
,使 ?若存在,求出直线
?若存在,求出直线 对应的函数关系式;若不存在,请说明理由.
对应的函数关系式;若不存在,请说明理由.

科目:czsx 来源:2005年全国中考数学试题汇编《一次函数》(05)(解析版) 题型:解答题
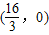 ,O为坐标原点.以AB为直径的⊙M与y轴的负半轴交于点D.
,O为坐标原点.以AB为直径的⊙M与y轴的负半轴交于点D.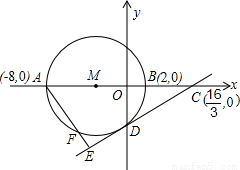
科目:czsx 来源:2005年全国中考数学试题汇编《圆》(12)(解析版) 题型:解答题
 ,O为坐标原点.以AB为直径的⊙M与y轴的负半轴交于点D.
,O为坐标原点.以AB为直径的⊙M与y轴的负半轴交于点D.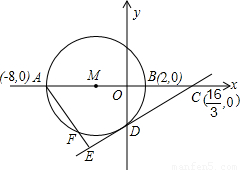
科目:czsx 来源: 题型:
 中,点A(2,m),B(-3,n)为两动点,其中m﹥1,连结
中,点A(2,m),B(-3,n)为两动点,其中m﹥1,连结 ,
, ,作
,作 轴于
轴于 点,
点, 轴于
轴于 点.
点.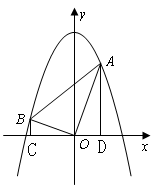
 时,抛物线经过
时,抛物线经过 两点且以
两点且以 轴为对称轴,求抛物线对应的二次函数的关系式
轴为对称轴,求抛物线对应的二次函数的关系式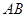 交
交 轴于点
轴于点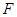 ,过点
,过点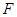 作直线
作直线 交抛物线于
交抛物线于 两点,问是否存在直线
两点,问是否存在直线 ,使S⊿POF:S⊿QOF=1:2?若存在,求出直线
,使S⊿POF:S⊿QOF=1:2?若存在,求出直线 对应的函数关系式;若不存在,请说明理由.
对应的函数关系式;若不存在,请说明理由. 科目:czsx 来源:四川省中考真题 题型:解答题
 ),现将纸片按如图折叠,AD,DE为折痕,∠OAD=30度,折叠后,点O落在点O1,点C落在线段AB点C1处,并且DO1与DC1在同一直线上。
),现将纸片按如图折叠,AD,DE为折痕,∠OAD=30度,折叠后,点O落在点O1,点C落在线段AB点C1处,并且DO1与DC1在同一直线上。