答案带解析】请画出适当的函数图象,求方程x2=x+3的解.答案解析
科目：czsx
来源：2012年人教版初中数学九年级下26.2用函数观点看一元二次方程练习卷（解析版）
题型：解答题
请画出适当的函数图象,求方程x2=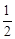
x+3的解.
查看答案和解析>>
科目：czsx
来源：
题型：
19、利用图象解一元二次方程x
2-2x-1=0时，我们采用的一种方法是：在直角坐标系中画出抛物线y=x
2和直线y=2x+1，两图象交点的横坐标就是该方程的解．
（1）请再给出一种利用图象求方程x
2-2x-1=0的解的方法；
（2）已知函数y=x
3的图象（如图）：求方程x
3-x-2=0的解．（结果保留2个有效数字）
查看答案和解析>>
科目：czsx
来源：2013-2014学年江苏省靖江市九年级上学期期末考试数学试卷（解析版）
题型：解答题
在平面直角坐标系xOy中，二次函数
的图象过A（-1，-2）、B（1，0）两点．
（1）求此二次函数的解析式并画出二次函数图象；
（2）点P(t,0)是x轴上的一个动点，过点P作x轴的垂线交直线AB于点M，交二次函数的图象于点N．当点M位于点N的上方时，直接写出t的取值范围．
查看答案和解析>>
科目：czsx
来源：浙江省宁波市2006年初中毕业生学业考试数学试题
题型：044
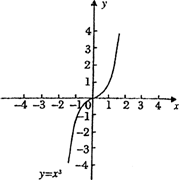
利用图象解一元二次方程x2－2x－1＝0时，我们采用的一种方法是：在直角坐标系中画出抛物线y＝x2和直线y＝2x＋1，两图象交点的横坐标就是该方程的解．
(1)请再给出一种利用图象求方程x2－2x－1＝0的解的方法
(2)已知函数y＝x3的图象(如图)：求方程x3－x－2＝0的解．(结果保留2个有效数字)
查看答案和解析>>
科目：czsx
来源：第23章《二次函数与反比例函数》中考题集（17）：23.4 二次函数与一元二次方程（解析版）
题型：解答题
利用图象解一元二次方程x
2-2x-1=0时，我们采用的一种方法是：在直角坐标系中画出抛物线y=x
2和直线y=2x+1，两图象交点的横坐标就是该方程的解．
（1）请再给出一种利用图象求方程x
2-2x-1=0的解的方法；
（2）已知函数y=x
3的图象（如图）：求方程x
3-x-2=0的解．（结果保留2个有效数字）
查看答案和解析>>
科目：czsx
来源：2006年全国中考数学试题汇编《二次函数》（04）（解析版）
题型：解答题
（2006•宁波）利用图象解一元二次方程x
2-2x-1=0时，我们采用的一种方法是：在直角坐标系中画出抛物线y=x
2和直线y=2x+1，两图象交点的横坐标就是该方程的解．
（1）请再给出一种利用图象求方程x
2-2x-1=0的解的方法；
（2）已知函数y=x
3的图象（如图）：求方程x
3-x-2=0的解．（结果保留2个有效数字）
查看答案和解析>>
科目：czsx
来源：第2章《二次函数》中考题集（20）：2.7 二次函数与一元二次方程（解析版）
题型：解答题
利用图象解一元二次方程x
2-2x-1=0时，我们采用的一种方法是：在直角坐标系中画出抛物线y=x
2和直线y=2x+1，两图象交点的横坐标就是该方程的解．
（1）请再给出一种利用图象求方程x
2-2x-1=0的解的方法；
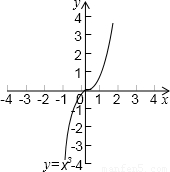
（2）已知函数y=x
3的图象（如图）：求方程x
3-x-2=0的解．（结果保留2个有效数字）
查看答案和解析>>
科目：czsx
来源：第26章《二次函数》中考题集（17）：26.2 用函数观点看一元二次方程（解析版）
题型：解答题
利用图象解一元二次方程x
2-2x-1=0时，我们采用的一种方法是：在直角坐标系中画出抛物线y=x
2和直线y=2x+1，两图象交点的横坐标就是该方程的解．
（1）请再给出一种利用图象求方程x
2-2x-1=0的解的方法；
（2）已知函数y=x
3的图象（如图）：求方程x
3-x-2=0的解．（结果保留2个有效数字）
查看答案和解析>>
科目：czsx
来源：
题型：解答题
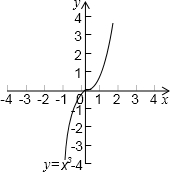
利用图象解一元二次方程x2-2x-1=0时，我们采用的一种方法是：在直角坐标系中画出抛物线y=x2和直线y=2x+1，两图象交点的横坐标就是该方程的解．
（1）请再给出一种利用图象求方程x2-2x-1=0的解的方法；
（2）已知函数y=x3的图象（如图）：求方程x3-x-2=0的解．（结果保留2个有效数字）
查看答案和解析>>
科目：czsx
来源：浙江省中考真题
题型：解答题
利用图象解一元二次方程x2-2x-1=0时，我们采用的一种方法是：在直角坐标系中画出抛物线y=x2和直线y=2x+1，两图象交点的横坐标就是该方程的解。
（1）请再给出一种利用图象求方程x2-2x-1=0的解的方法；
（2）已知函数y=x3的图象（如图）：求方程x3-x-2=0的解。（结果保留2个有效数字）
查看答案和解析>>
科目：czsx
来源：第2章《二次函数》中考题集（20）：2.4 二次函数的应用（解析版）
题型：解答题
利用图象解一元二次方程x
2-2x-1=0时，我们采用的一种方法是：在直角坐标系中画出抛物线y=x
2和直线y=2x+1，两图象交点的横坐标就是该方程的解．
（1）请再给出一种利用图象求方程x
2-2x-1=0的解的方法；
（2）已知函数y=x
3的图象（如图）：求方程x
3-x-2=0的解．（结果保留2个有效数字）
查看答案和解析>>
科目：czsx
来源：第2章《二次函数》中考题集（52）：2.8 二次函数与一元二次方程（解析版）
题型：解答题
利用图象解一元二次方程x
2-2x-1=0时，我们采用的一种方法是：在直角坐标系中画出抛物线y=x
2和直线y=2x+1，两图象交点的横坐标就是该方程的解．
（1）请再给出一种利用图象求方程x
2-2x-1=0的解的方法；
（2）已知函数y=x
3的图象（如图）：求方程x
3-x-2=0的解．（结果保留2个有效数字）
查看答案和解析>>
科目：czsx
来源：第2章《二次函数》中考题集（21）：2.3 二次函数的应用（解析版）
题型：解答题
利用图象解一元二次方程x
2-2x-1=0时，我们采用的一种方法是：在直角坐标系中画出抛物线y=x
2和直线y=2x+1，两图象交点的横坐标就是该方程的解．
（1）请再给出一种利用图象求方程x
2-2x-1=0的解的方法；
（2）已知函数y=x
3的图象（如图）：求方程x
3-x-2=0的解．（结果保留2个有效数字）
查看答案和解析>>
科目：czsx
来源：第34章《二次函数》中考题集（22）：34.4 二次函数的应用（解析版）
题型：解答题
利用图象解一元二次方程x
2-2x-1=0时，我们采用的一种方法是：在直角坐标系中画出抛物线y=x
2和直线y=2x+1，两图象交点的横坐标就是该方程的解．
（1）请再给出一种利用图象求方程x
2-2x-1=0的解的方法；
（2）已知函数y=x
3的图象（如图）：求方程x
3-x-2=0的解．（结果保留2个有效数字）
查看答案和解析>>
科目：czsx
来源：第27章《二次函数》中考题集（21）：27.3 实践与探索（解析版）
题型：解答题
利用图象解一元二次方程x
2-2x-1=0时，我们采用的一种方法是：在直角坐标系中画出抛物线y=x
2和直线y=2x+1，两图象交点的横坐标就是该方程的解．
（1）请再给出一种利用图象求方程x
2-2x-1=0的解的方法；
（2）已知函数y=x
3的图象（如图）：求方程x
3-x-2=0的解．（结果保留2个有效数字）
查看答案和解析>>
科目：czsx
来源：2006年浙江省宁波市中考数学试卷（课标卷）（解析版）
题型：解答题
（2006•宁波）利用图象解一元二次方程x
2-2x-1=0时，我们采用的一种方法是：在直角坐标系中画出抛物线y=x
2和直线y=2x+1，两图象交点的横坐标就是该方程的解．
（1）请再给出一种利用图象求方程x
2-2x-1=0的解的方法；
（2）已知函数y=x
3的图象（如图）：求方程x
3-x-2=0的解．（结果保留2个有效数字）
查看答案和解析>>
科目：czsx
来源：第20章《二次函数和反比例函数》中考题集（19）：20.5 二次函数的一些应用（解析版）
题型：解答题
利用图象解一元二次方程x
2-2x-1=0时，我们采用的一种方法是：在直角坐标系中画出抛物线y=x
2和直线y=2x+1，两图象交点的横坐标就是该方程的解．
（1）请再给出一种利用图象求方程x
2-2x-1=0的解的方法；
（2）已知函数y=x
3的图象（如图）：求方程x
3-x-2=0的解．（结果保留2个有效数字）
查看答案和解析>>
科目：czsx
来源：
题型：
26、一物体从高处落到地面，它落下的高度与经过的时间如下关系：
| 时间t（s） |
0.5 |
0.6 |
0.7 |
1 |
1.5 |
2 |
| 高度h（m） |
5×0.25 |
5×0.36 |
5×0.49 |
5×1 |
5×2.25 |
5×4 |
（1）物体下落1.2s时的落下高度为
7.2m
（2）用时间t（s）表示高度h（m）的关系式为
h=5t2
（3）当物体下落到33.8m时所用的时间为
2.6秒
（4）请画出适当的统计图表示上表．
查看答案和解析>>
科目：czsx
来源：学习周报 数学 北师大九年级版 2009－2010学年 第25期 总第181期 北师大版
题型：044
已知二次函数y＝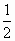
x2＋bx＋c的图象经过A(c，－2)，
．
求证：这个二次函数的对称轴是x＝3．
题目中的矩形阴影部分是一段被墨水污染无法辨认的文字．
(1)根据题目中的现有信息，你能否求出二次函数表达式？若能，请写出解答过程，并画出二次函数图象；若不能，请说明理由．
(2)请你根据已有的信息，在原题的矩形阴影中，填上一个适当的条件，把原题补充完整．
查看答案和解析>>
