科目:czsx 来源: 题型:
科目:czsx 来源: 题型:
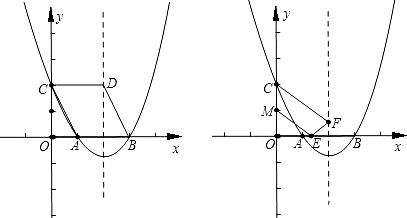
 AB=5OB,设点E(x,y)是抛物线上一动点,且位于第四象限,四边形OEAF是以OA为对角线的平行四边形.
AB=5OB,设点E(x,y)是抛物线上一动点,且位于第四象限,四边形OEAF是以OA为对角线的平行四边形.科目:czsx 来源: 题型:
科目:czsx 来源:2011-2012学年广西省贵港市中考模拟试题数学试卷(一) 题型:解答题
如图,已知抛物线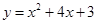 交
交 轴于A、B两点,交
轴于A、B两点,交 轴于点C,抛物线的对称轴交
轴于点C,抛物线的对称轴交 轴于点E,点B的坐标为(
轴于点E,点B的坐标为(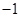 ,0).
,0).

1.求抛物线的对称轴及点A的坐标
2.在平面直角坐标系 中是否存在点P,与A、B、C三点构成一个平行四边形?若存在,请写出点P的坐标;若不存在,请说明理由;
中是否存在点P,与A、B、C三点构成一个平行四边形?若存在,请写出点P的坐标;若不存在,请说明理由;
3.连结CA与抛物线的对称轴交于点D,在抛物线上是否存在点M,使得直线CM把四边形DEOC分成面积相等的两部分?若存在,请求出直线CM的解析式;若不存在,请说明理由.
科目:czsx 来源:2012年5月广东省深圳市中考数学模拟试卷(三)(解析版) 题型:解答题

科目:czsx 来源:2012年辽宁省锦州市中考数学二模试卷(解析版) 题型:解答题

科目:czsx 来源:北京期末题 题型:解答题
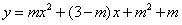 交x轴于C(x1,0),D(x2,0)两点,(x1<x2)且
交x轴于C(x1,0),D(x2,0)两点,(x1<x2)且

 的面积为S,求S与a之间的函数关系式。
的面积为S,求S与a之间的函数关系式。 科目:czsx 来源: 题型:解答题

科目:czsx 来源: 题型:
(本题满分12分)已知抛物线![]() 交x轴于A(1,0)、B(3,0)两点,交y轴于点C,其顶点为D.
交x轴于A(1,0)、B(3,0)两点,交y轴于点C,其顶点为D.
(1)求b、c的值并写出抛物线的对称轴;
(2)连接BC,过点O作直线OE⊥BC交抛物线的对称轴于点E.
求证:四边形ODBE是等腰梯形;
(3)抛物线上是否存在点Q,使得△OBQ的面积等于四边形ODBE的面积的![]() ?若存在,求点Q的坐标;若不存在,请说明理由.
?若存在,求点Q的坐标;若不存在,请说明理由.
科目:czsx 来源: 题型:解答题
 AB=5OB,设点E(x,y)是抛物线上一动点,且位于第四象限,四边形OEAF是以OA为对角线的平行四边形.
AB=5OB,设点E(x,y)是抛物线上一动点,且位于第四象限,四边形OEAF是以OA为对角线的平行四边形.科目:czsx 来源: 题型:
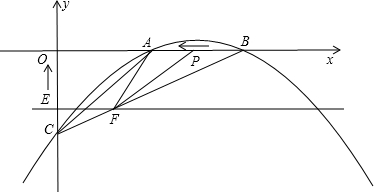
如图,已知抛物线![]() 交x轴于C(x1,0),D(x2,0)两点,(x1<x2)且
交x轴于C(x1,0),D(x2,0)两点,(x1<x2)且![]()
(1)试确定m的值;
(2)过点A(-1,-5)和抛物线的顶点M的直线交x轴于点B,求B点的坐标;
(3)设点P(a,b)是抛物线上点C到点M之间的一个动点(含C、M点),![]() 是以PO为腰、底边OQ在x轴上的等腰三角形,过点Q作x轴的垂线交直线AM于点R,连结PR。设
是以PO为腰、底边OQ在x轴上的等腰三角形,过点Q作x轴的垂线交直线AM于点R,连结PR。设![]() 的面积为S,求S与a之间的函数关系式。
的面积为S,求S与a之间的函数关系式。
科目:czsx 来源:2013-2014学年四川省成都市武侯区九年级上学期期末考试数学试卷(解析版) 题型:解答题
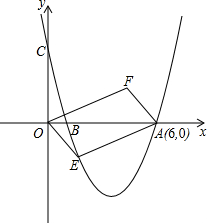
如图,在平面直角坐标系中,已知抛物线 交
交 轴于A(2,0),B(6,0)两点,交
轴于A(2,0),B(6,0)两点,交 轴于点C(0,
轴于点C(0, ).
).

(1)求此抛物线的解析式;
(2)若此抛物线的对称轴与直线 交于点D,作⊙D与x轴相切,⊙D交
交于点D,作⊙D与x轴相切,⊙D交 轴于点E、F两点,求劣弧EF所对圆心角的度数;
轴于点E、F两点,求劣弧EF所对圆心角的度数;
(3)P为此抛物线在第二象限图像上的一点,PG垂直于 轴,垂足为点G,试确定P点的位置,使得△PGA的面积被直线AC分为1︰2两部分.
轴,垂足为点G,试确定P点的位置,使得△PGA的面积被直线AC分为1︰2两部分.
科目:czsx 来源:2013年4月中考数学模拟试卷(8)(解析版) 题型:解答题

科目:czsx 来源:2011-2012学年江苏省南通市九年级(上)期末数学试卷(解析版) 题型:解答题
 交x轴于A、B两点,交y轴于C点,且Rt△AOC∽Rt△COB,求△ABC的面积.
交x轴于A、B两点,交y轴于C点,且Rt△AOC∽Rt△COB,求△ABC的面积.
科目:czsx 来源: 题型:
如图,已知抛物线![]() 交
交![]() 轴于A、B两点,交
轴于A、B两点,交![]() 轴于点C,抛物线的对称轴交
轴于点C,抛物线的对称轴交![]() 轴于点E,点B的坐标为(
轴于点E,点B的坐标为(![]() ,0).
,0).

1.求抛物线的对称轴及点A的坐标
2.在平面直角坐标系![]() 中是否存在点P,与A、B、C三点构成一个平行四边形?若存在,请写出点P的坐标;若不存在,请说明理由;
中是否存在点P,与A、B、C三点构成一个平行四边形?若存在,请写出点P的坐标;若不存在,请说明理由;
3.连结CA与抛物线的对称轴交于点D,在抛物线上是否存在点M,使得直线CM把四边形DEOC分成面积相等的两部分?若存在,请求出直线CM的解析式;若不存在,请说明理由.
科目:czsx 来源:2012年人教新课标版中考综合模拟数学卷(11) 题型:计算题
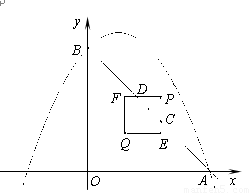
如图,已知抛物线 交x轴的正半轴于点A,交y轴于点B.
交x轴的正半轴于点A,交y轴于点B.
【小题1】求A、B两点的坐标,并求直线AB的解析式;
【小题2】设 (
( )是直线
)是直线 上的一点,Q是OP的中点(O是原点),以PQ为对角线作正方形PEQF.若正方形PEQF与直线AB有公共点,求x的取值范围;
上的一点,Q是OP的中点(O是原点),以PQ为对角线作正方形PEQF.若正方形PEQF与直线AB有公共点,求x的取值范围;
【小题3】在(2)的条件下,记正方形PEQF与△OAB公共部分的面积为S,求S关于x的函数解析式,并探究S的最大值.
科目:czsx 来源: 题型:
如图,在平面直角坐标系中,已知抛物线![]() 交
交![]() 轴于
轴于![]() 两点,交
两点,交![]() 轴于点
轴于点![]() .
.
(1)求此抛物线的解析式;
![]() (2)若此抛物线的对称轴与直线
(2)若此抛物线的对称轴与直线![]() 交于点D,作⊙D与x轴相切,⊙D交
交于点D,作⊙D与x轴相切,⊙D交![]() 轴于点E、F两点,求劣弧EF的长;
轴于点E、F两点,求劣弧EF的长;
(3)P为此抛物线在第二象限图像上的一点,PG垂直于![]() 轴,垂足为点G,试确定P点的位置,使得△PGA的面积被直线AC分为1︰2两部分.
轴,垂足为点G,试确定P点的位置,使得△PGA的面积被直线AC分为1︰2两部分.
 |
科目:czsx 来源:2013届江苏阜宁第一学期期末学情调研九年级数学试卷 题型:解答题
如图,在平面直角坐标系中,已知抛物线 交
交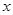 轴于
轴于 两点,交
两点,交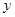 轴于点
轴于点 .
.

(1)求此抛物线的解析式;
(2)若此抛物线的对称轴与直线 交于点D,作⊙D与x轴相切,⊙D交
交于点D,作⊙D与x轴相切,⊙D交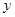 轴于点E、F两点,求劣弧
轴于点E、F两点,求劣弧  的长;
的长;
(3)P为此抛物线在第二象限图像上的一点,PG垂直于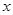 轴,垂足为点G,试确定P点的位置,使得△PGA的面积被直线AC分为1︰2两部分.
轴,垂足为点G,试确定P点的位置,使得△PGA的面积被直线AC分为1︰2两部分.
科目:czsx 来源:2012-2013学年江苏阜宁第一学期期末学情调研九年级数学试卷 题型:解答题
如图,在平面直角坐标系中,已知抛物线 交
交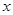 轴于
轴于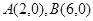 两点,交
两点,交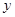 轴于点
轴于点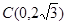 .
.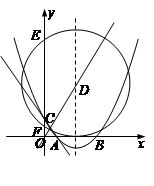
(1)求此抛物线的解析式;
(2)若此抛物线的对称轴与直线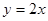 交于点D,作⊙D与x轴相切,⊙D交
交于点D,作⊙D与x轴相切,⊙D交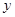 轴于点E、F两点,求劣弧
轴于点E、F两点,求劣弧 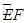 的长;
的长;
(3)P为此抛物线在第二象限图像上的一点,PG垂直于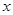 轴,垂足为点G,试确定P点的位置,使得△PGA的面积被直线AC分为1︰2两部分.
轴,垂足为点G,试确定P点的位置,使得△PGA的面积被直线AC分为1︰2两部分.
科目:czsx 来源:2012年人教新课标版中考综合模拟数学卷(11) 题型:解答题
如图,已知抛物线 交x轴的正半轴于点A,交y轴于点B.
交x轴的正半轴于点A,交y轴于点B.
1.求A、B两点的坐标,并求直线AB的解析式;
2.设 (
( )是直线
)是直线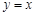 上的一点,Q是OP的中点(O是原点),以PQ为对角线作正方形PEQF.若正方形PEQF与直线AB有公共点,求x的取值范围;
上的一点,Q是OP的中点(O是原点),以PQ为对角线作正方形PEQF.若正方形PEQF与直线AB有公共点,求x的取值范围;
3.在(2)的条件下,记正方形PEQF与△OAB公共部分的面积为S,求S关于x的函数解析式,并探究S的最大值.