科目：czsx 来源： 题型：
二次函数y=ax2+bx+c的图形如图所示，下列结论：科目：czsx 来源：2009-2010学年福建省南平市剑津中学九年级（上）期中数学试卷（解析版） 题型：填空题
科目：czsx 来源： 题型：填空题
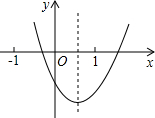二次函数y=ax2+bx+c的图形如图所示，下列结论：科目：czsx 来源： 题型：
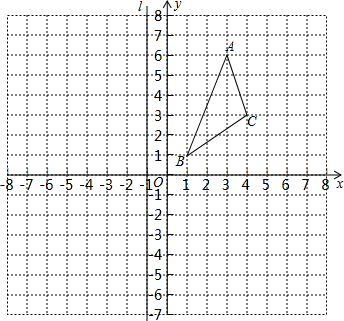（2012•溧水县二模）△ABC在直角坐标系中的位置如图所示，直线l经过点（-1，0），并且与y轴平行．科目：czsx 来源： 题型：044
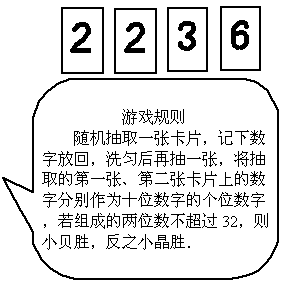
(2007，辽宁省十二市，23)四张质地相同的卡片如图所示．将卡片洗匀后，背面朝上放置在桌面上．
(1)求随机抽取一张卡片，恰好得到数字2的概率；
(2)小贝和小晶想用以上四张卡片做游戏，游戏规则见信息图．你认为这个游戏公平吗？请用列表法或画树状图法说明理由，若认为不公平，请你修改规则，使游戏变得公平．
科目：czsx 来源：同步题 题型：填空题
科目：czsx 来源： 题型：填空题
张同学是一个NBA迷，周末的一天他在家里做作业，一次他抬头看到墙上镜面里的钟如图所示，那他过________分钟可以去看9：30的一场火箭VS骑士．科目：czsx 来源： 题型：
小明、小亮两人在一次赛跑中，路程与时间的关系如图所示，下列说法中不正确的是( )
A．小明获胜 B．这是一次100m赛跑
C．小明的速度是12m／s D．小亮100m的成绩是12.5s
科目：czsx 来源：2011-2012年浙江省衢州华外九年级上学期第二次质量检测数学卷 题型：解答题
（本题10分）问题情境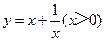
已知矩形的面积为a（a为常数，a＞0），当该矩形的长为多少时，它的周长最小？最小值是多少？
数学模型
设该矩形的一边长为x，周长为y，则y与x的函数关系式为 ．
探索研究
⑴我们可以借鉴以前研究函数的经验，先探索函数的图象性质．
①填写下表，画出函数的图象：
| x | …… |  |  |  | 1 | 2 | 3 | 4 | …… |
| y | …… | | | | | | | | …… |
|
科目：czsx 来源：2013-2014学年广东省广州市海珠区九年级上学期期末数学试卷（解析版） 题型：选择题
已知二次函数y=ax²+bx+c(a≠0)的图像如图所示，则下列结论中正确的是（ ）
A.a＞0 B.3是方程ax²+bx+c=0的一个根
C.a+b+c=0 D.当x＜1时，y随x的增大而减小
科目：czsx 来源： 题型：
（本题10分）问题情境
已知矩形的面积为a（a为常数，a＞0），当该矩形的长为多少时，它的周长最小？最小值是多少？
数学模型
设该矩形的一边长为x，周长为y，则y与x的函数关系式为 ．
探索研究
⑴我们可以借鉴以前研究函数的经验，先探索函数的图象性质．
①填写下表，画出函数的图象：
| x | …… |
|
|
| 1 | 2 | 3 | 4 | …… |
| y | …… |
|
|
|
|
|
|
| …… |
|
③在求二次函数y=ax＋bx＋c（a≠0）的最大（小）值时，除了通过观察图象，还可以通过
配方得到．请你通过配方求函数(x＞0)的最小值．
解决问题
⑵用上述方法解决“问题情境”中的问题，直接写出答案．
科目：czsx 来源：2011-2012年浙江省衢州华外九年级上学期第二次质量检测数学卷 题型：解答题
（本题10分）问题情境
已知矩形的面积为a（a为常数，a＞0），当该矩形的长为多少时，它的周长最小？最小值是多少？
数学模型
设该矩形的一边长为x，周长为y，则y与x的函数关系式为 ．
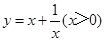探索研究
⑴我们可以借鉴以前研究函数的经验，先探索函数的图象性质．
①填写下表，画出函数的图象：
|
x |
…… |
|
|
|
1 |
2 |
3 |
4 |
…… |
|
y |
…… |
|
|
|
|
|
|
|
…… |
|
③在求二次函数y=ax＋bx＋c（a≠0）的最大（小）值时，除了通过观察图象，还可以通过
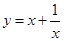
配方得到．请你通过配方求函数(x＞0)的最小值．
解决问题
⑵用上述方法解决“问题情境”中的问题，直接写出答案．
科目：czsx 来源： 题型：
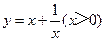
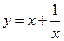
| x | …… | 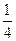 | 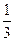 | 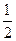 | 1 | 2 | 3 | 4 | …… |
| y | …… | | | | | | | | …… |
|
科目：czsx 来源： 题型：
下面是一个二次函数y=ax
＋bx＋c的自变量x和函数y的对应值表：
| x | … | －3 | －2 | －1 | 0 | 1 | 2 | 3 | … |
| y | … | 12 | 5 | 0 | －3 | －4 | －3 | 0 | … |
根据表中提供的信息解答下列各题：
（1）求抛物线与y轴的交点坐标；
（2）抛物线的对称轴是在y轴的右边还是左边？并说明理由
（3）设抛物线与x轴两个交点分别为A、B，顶点为C，求△ABC的面积.
科目：czsx 来源： 题型：
已知二次函数y=ax²+bx+c（c≠0）的图像如图4所示，下列说法错误的是：
（A）图像关于直线x=1对称
（B）函数y=ax²+bx+c（c ≠0）的最小值是 -4
（C）-1和3是方程ax²+bx+c=0（c ≠0）的两个根
（D）当x＜1时，y随x的增大而增大
（2013•平阳县二模）三角形在方格纸中的位置如图所示，则cosα的值是（ ）
13、张同学是一个NBA迷，周末的一天他在家里做作业，一次他抬头看到墙上镜面里的钟如图所示，那他过
