精英家教网 >
试题搜索列表 >抛物线y=ax2+bx+c与直线y=x-2相交于（m，-2）（n,3）两点，且抛物线的对称轴为直线x=3
抛物线y=ax2+bx+c与直线y=x-2相交于（m，-2）（n,3）两点，且抛物线的对称轴为直线x=3答案解析
科目：czsx
来源：河南省同步题
题型：解答题
抛物线y=ax2+bx+c与直线y=x-2相交于（m，-2），（n，3）两点，且抛物线的对称轴为直线x=3，求抛物线的解析式。
查看答案和解析>>
科目：czsx
来源：
题型：
已知抛物线y=ax2+bx+c与直线y=kx+4相交于A（1，m），B（4，8）两点，与x轴交于原点O及点C．
（1）求直线与抛物线相应的函数关系式；
（2）在x轴上方的抛物线上是否存在点D，使得S△OCD=S△OCB？如果存在，请求出满足条件的点D；如果不存在，请说明理由．
查看答案和解析>>
科目：czsx
来源：
题型：
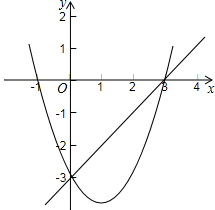
如图，抛物线y
1=ax
2+bx+c与直线y
2=kx+h相交于（3，0）、（0，-3）两点，当y
1＞y
2时，自变量x的取值范围是（ ）
查看答案和解析>>
科目：czsx
来源：
题型：
已知抛物线y=ax
2+bx+c与直线y=mx+n相交于两点，这两点的坐标分别是（0，-
）和（m-b，
m
2-mb+n），其中 a，b，c，m，n为实数，且a，m不为0．
（1）求c的值；
（2）设抛物线y=ax
2+bx+c与x轴的两个交点是（x
1，0）和（x
2，0），求x
1▪x
2的值；
（3）当-1≤x≤1时，设抛物线y=ax
2+bx+c上与x轴距离最大的点为P（x
0，y
0），求这时|y
0丨的最小值．
查看答案和解析>>
科目：czsx
来源：
题型：解答题
已知抛物线y=ax2+bx+c与直线y=kx+4相交于A（1，m），B（4，8）两点，与x轴交于原点O及点C．
（1）求直线与抛物线相应的函数关系式；
（2）在x轴上方的抛物线上是否存在点D，使得S△OCD=S△OCB？如果存在，请求出满足条件的点D；如果不存在，请说明理由．
查看答案和解析>>
科目：czsx
来源：不详
题型：解答题
已知抛物线y=ax2+bx+c与直线y=kx+4相交于A（1，m），B（4，8）两点，与x轴交于原点O及点C．
（1）求直线与抛物线相应的函数关系式；
（2）在x轴上方的抛物线上是否存在点D，使得S△OCD=S△OCB？如果存在，请求出满足条件的点D；如果不存在，请说明理由．
查看答案和解析>>
科目：czsx
来源：《第2章 二次函数》2009年单元测试（解析版）
题型：解答题
已知抛物线y=ax2+bx+c与直线y=kx+4相交于A（1，m），B（4，8）两点，与x轴交于原点O及点C．
（1）求直线与抛物线相应的函数关系式；
（2）在x轴上方的抛物线上是否存在点D，使得S△OCD=S△OCB？如果存在，请求出满足条件的点D；如果不存在，请说明理由．
查看答案和解析>>
科目：czsx
来源：湖北省中考真题
题型：解答题
已知抛物线y=ax2+bx+c与直线y=mx+n相交于两点，这两点的坐标分别是（0，-
）和（m-b，m2-mb+n），其中a，b，c，m，n为实数，且a，m不为0。
（1）求c的值；
（2）设抛物线y=ax2+bx+c与x轴的两个交点是（x1，0）和（x2，0），求x1x2的值；
（3）当-1≤x≤1时，设抛物线y=ax2+bx+c上与x轴距离最大的点为P（x0，y0），求这时|y0|的最小值。
查看答案和解析>>
科目：czsx
来源：2011年湖北省宜昌市中考数学试卷（解析版）
题型：解答题
已知抛物线y=ax
2+bx+c与直线y=mx+n相交于两点，这两点的坐标分别是（0，-
）和（m-b，m
2-mb+n），其中 a，b，c，m，n为实数，且a，m不为0．
（1）求c的值；
（2）设抛物线y=ax
2+bx+c与x轴的两个交点是（x
1，0）和（x
2，0），求x
1▪x
2的值；
（3）当-1≤x≤1时，设抛物线y=ax
2+bx+c上与x轴距离最大的点为P（x
，y
），求这时|y
丨的最小值．
查看答案和解析>>
科目：czsx
来源：
题型：单选题
如图，抛物线y1=ax2+bx+c与直线y2=kx+h相交于（3，0）、（0，-3）两点，当y1＞y2时，自变量x的取值范围是
- A.
-1＜x＜3
- B.
x＞3或x＜-1
- C.
-3＜x＜3
- D.
x＞3或x＜0
查看答案和解析>>
科目：czsx
来源：
题型：
（2013•平阳县二模）如图，抛物线
y=ax2+bx+与直线AB交于点A（-1，0），B（4，
）．点D是抛物线A，B两点间部分上的一个动点（不与点A，B重合），直线CD与y轴平行，交直线AB于点C，连接AD，BD．
（1）求抛物线的解析式；
（2）①当D为抛物线顶点时，线段DC的长度是多少？
②设点D的横坐标为m，△ADB的面积为S，求S关于m的函数关系式，并求出S的最大值．
查看答案和解析>>
科目：czsx
来源：
题型：
15、抛物线y=ax2+bx+c与直线y=ax+b的大致图象只可能是（ ）
查看答案和解析>>
科目：czsx
来源：
题型：
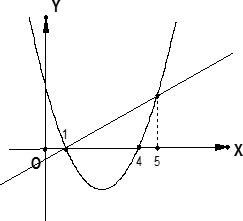
抛物线y
1=ax
2+bx+c与直线y
2=kx+m的图象如图所示，根据图象回答下列问题：
（1）指出b，b
2-4ac，a-b+c的符号；
（2）若y
1＜0，指出x的取值范围；
（3）若y
1＞y
2，指出x的取值范围．
查看答案和解析>>
科目：czsx
来源：
题型：
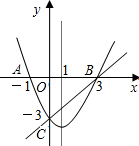
如图，抛物线y=ax
2+bx+c与直线y=kx+m在同一直角坐标系中，二次函数的图象与两坐标轴分别交于A（-1，0）、点B（3，0）和点C（0，-3），一次函数的图象与抛物线交于B、C两点．当x满足：
时一次函数值大于二次函数的值．
查看答案和解析>>
科目：czsx
来源：
题型：
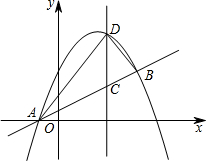
（2013•郑州模拟）如图，抛物线
y=ax2+bx+与直线AB交于点A（-1，0），B（4，
）．点D是抛物线A，B两点间部分上的一个动点（不与点A，B重合），直线CD与y轴平行，交直线AB于点C，连接AD，BD．
（1）求抛物线的解析式；
（2）设点D的横坐标为m，△ADB的面积为S，求S关于m的函数关系式，并求出当S取最大值时的点C的坐标；
（3）当点D为抛物线的顶点时，若点P是抛物线上的动点，点Q是直线AB上的动点，判断有几个位置能使以点P，Q，C，D为顶点的四边形为平行四边形，直接写出相应的点Q的坐标．
查看答案和解析>>
科目：czsx
来源：
题型：
已知：抛物线y=ax
2+bx+c与y交于C点，顶点为M，直线CM的解析式为y=-x+3并且线段CM的长为
3，则抛物线的解析式为
．
查看答案和解析>>
科目：czsx
来源：
题型：
已知抛物线y=ax
2+bx+c与直线y=25有公共点，且仅当
-＜x＜时抛物线在x轴上方，求a、b、c的取值范围．
查看答案和解析>>
科目：czsx
来源：
题型：
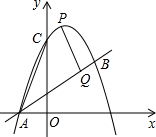
如图，抛物线y=ax
2+bx+
与直线AB
y=x+交于x轴上的一点A，和另一点B（4，n）．点P是抛物线A，B两点间部分上的一个动点（不与点A，B重合），直线PQ与直线AB垂直，交直线AB于点Q，．
（1）求抛物线的解析式和cos∠BAO的值；
（2）设点P的横坐标为m用含m的代数式表示线段PQ的长，并求出线段PQ长的最大值；
（3）点E是抛物线上一点，过点E作EF∥AC，交直线AB与点F，若以E、F、A、C为顶点的四边形为平行四边形，直接写出相应的点E的坐标．
查看答案和解析>>
科目：czsx
来源：
题型：
（2012•湖里区一模）已知：直线y=
x+c与x轴交于点A，与y轴交于点B，抛物线y=ax
2+bx+4c与直线AB交于A、D两点，与y轴交于点C．
（1）若c=-1，点C为抛物线的顶点，求点D的坐标；
（2）若c＞0，点O到直线AB的距离为
，∠CDB=∠ACB，求抛物线的解析式．
查看答案和解析>>
科目：czsx
来源：
题型：
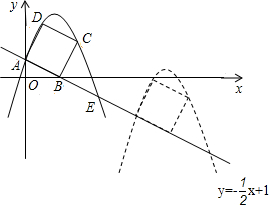
如图，已知直线
y=-x+1分别交y轴、x轴于A，B两点，以线段AB为边向上作正方形ABCD过点A，D，C的抛物线y=ax
2+bx+1与直线的另一交点为点E
（1）点C的坐标为
；点D的坐标为
．并求出抛物线的解析式；
（2）若正方形以每秒
个单位长度的速度沿射线AB下滑，直至顶点D落在x轴上时停止．设正方形落在x轴下方部分的面积为S，求S关于滑行时间t的函数关系式，并写出相应自变量t的取值范围；
（3）在（2）的条件下，抛物线与正方形一起平移，同时停止，求抛物线上C，E两点间的抛物线弧所扫过的面积．
查看答案和解析>>
