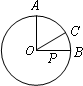精英家教网 >
试题搜索列表 >如图,A、B是直线L同侧的两定点,定长线段PQ在L上平行移动,问PQ移动到什么位置时,AP+PQ+QB的长最短?、
如图,A、B是直线L同侧的两定点,定长线段PQ在L上平行移动,问PQ移动到什么位置时,AP+PQ+QB的长最短?、答案解析
科目:czsx
来源:
题型:
几何模型:条件:如图,A、B是直线l同旁的两个定点.
问题:在直线l上确定一点P,使PA+PB的值最小.
方法:作点A关于直线l的对称点A′,连接A′B交l于点P,则PA+PB=A′P+PB=A′B,
由“两点之间,线段最短”可知,点P即为所求的点.
模型应用:
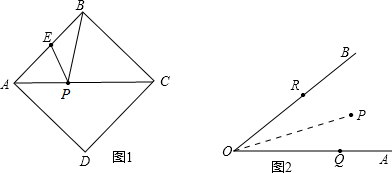
(1)如图1,正方形ABCD的边长为2,E为AB的中点,P是AC上一动点.则PB+PE的最小值是
;
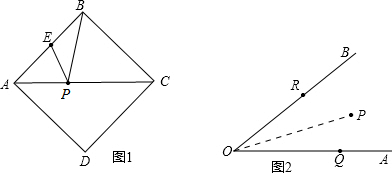
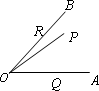
(2)如图2,∠AOB=45°,P是∠AOB内一定点,PO=10,Q、R分别是OA、OB上的动点,求△PQR周长的最小值.(要求画出示意图,写出解题过程)
查看答案和解析>>
科目:czsx
来源:
题型:

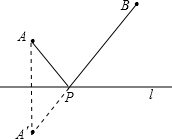
几何模型:
条件:如图,A、B是直线l同旁的两个定点.
问题:在直线l上确定一点P,使PA+PB的值最小.
方法:作点A关于直线l的对称点A
′,连接A′B交l于点P,则PA+PB=A′B的值最小(不必证明).
模型应用:
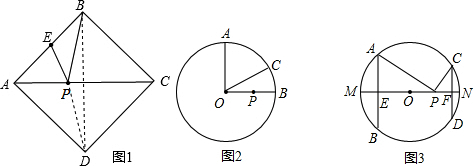
(1)如图1,正方形ABCD的边长为2,E为AB的中点,P是AC上一动点.连接BD,由正方形对称性可知,B与D关于直线AC对称.连接ED交AC于P,则PB+PE的最小值是
;
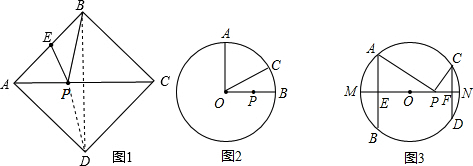
(2)如图2,⊙O的半径为2,点A、B、C在⊙O上,OA⊥OB,∠AOC=60°,P是OB上一动点,求PA+PC的最小值;
(3)如图3,AB、CD是半径为5的⊙O的两条弦,AB=8,CD=6,MN是直径,AB⊥MN于点E,CD⊥MN于点F,P为EF上的任意一点,求PA+PC的最小值.
查看答案和解析>>
科目:czsx
来源:期中题
题型:解答题
阅读理解题:【几何模型】
条件:如图,A、B是直线l同旁的两个定点,问题:在直线l上确定一点P,使PA+PB的值最小。
方法:作点A关于直线l的对称点A′,连接A′B交l于点P,则PA+PB=A′P+PB=A′B,由“两点之间,线段最短”可知,点P即为所求的点。
【模型应用】
(1)如图1,正方形ABCD的边长为2,E为AB的中点,P是AC上一动点.求出PB+PE的最小值。(画出示意图,并解答)
(2)如图2,∠AOB=45°,P是∠AOB内一定点,PO=10,Q、R分别是OA、OB上的动点,求△PQR周长的最小值。(要求画出示意图,写出解题过程)
查看答案和解析>>
科目:czsx
来源:
题型:解答题
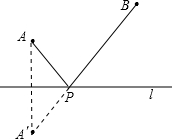 几何模型:条件:如图,A、B是直线l同旁的两个定点.
几何模型:条件:如图,A、B是直线l同旁的两个定点.
问题:在直线l上确定一点P,使PA+PB的值最小.
方法:作点A关于直线l的对称点A′,连接A′B交l于点P,则PA+PB=A′P+PB=A′B,
由“两点之间,线段最短”可知,点P即为所求的点.
模型应用:
(1)如图1,正方形ABCD的边长为2,E为AB的中点,P是AC上一动点.则PB+PE的最小值是______;
(2)如图2,∠AOB=45°,P是∠AOB内一定点,PO=10,Q、R分别是OA、OB上的动点,求△PQR周长的最小值.(要求画出示意图,写出解题过程)
查看答案和解析>>
科目:czsx
来源:
题型:解答题
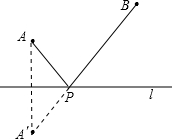 几何模型:
几何模型:
条件:如图,A、B是直线l同旁的两个定点.
问题:在直线l上确定一点P,使PA+PB的值最小.
方法:作点A关于直线l的对称点A′,连接A′B交l于点P,则PA+PB=A′B的值最小(不必证明).
模型应用:
(1)如图1,正方形ABCD的边长为2,E为AB的中点,P是AC上一动点.连接BD,由正方形对称性可知,B与D关于直线AC对称.连接ED交AC于P,则PB+PE的最小值是______;
(2)如图2,⊙O的半径为2,点A、B、C在⊙O上,OA⊥OB,∠AOC=60°,P是OB上一动点,求PA+PC的最小值;
(3)如图3,AB、CD是半径为5的⊙O的两条弦,AB=8,CD=6,MN是直径,AB⊥MN于点E,CD⊥MN于点F,P为EF上的任意一点,求PA+PC的最小值.
查看答案和解析>>
科目:czsx
来源:2011-2012学年浙江省杭州市开元中学九年级(下)第一次月考数学试卷(解析版)
题型:解答题
几何模型:
条件:如图,A、B是直线l同旁的两个定点.
问题:在直线l上确定一点P,使PA+PB的值最小.
方法:作点A关于直线l的对称点A
′,连接A′B交l于点P,则PA+PB=A′B的值最小(不必证明).
模型应用:
(1)如图1,正方形ABCD的边长为2,E为AB的中点,P是AC上一动点.连接BD,由正方形对称性可知,B与D关于直线AC对称.连接ED交AC于P,则PB+PE的最小值是______

查看答案和解析>>
科目:czsx
来源:
题型:
几何模型:
条件:如下图,A、B是直线l同旁的两个定点.
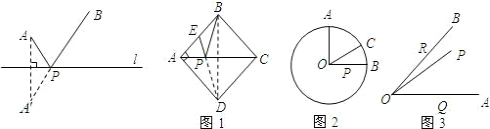
问题:在直线l上确定一点P,使PA+PB的值最小.
方法:作点A关于直线l的对称点A′,连接A′B交l于点P,则PA+PB=A′B的值最小(不必证明).
模型应用:
(1)如图1,正方形ABCD的边长为2,E为AB的中点,P是AC上一动点.连接BD,由正方形对称性可知,B与D关于直线AC对称.连接ED交AC于P,则PB+PE的最小值是
;
(2)如图2,⊙O的半径为2,点A、B、C在⊙O上,OA⊥OB,∠AOC=60°,P是OB上一动点,求PA+PC的最小值;
(3)如图3,∠AOB=45°,P是∠AOB内一点,PO=10,Q、R分别是OA、OB上的动点,求△PQR周长的最小值.
查看答案和解析>>
科目:czsx
来源:2009年全国中考数学试题汇编《图形的对称》(04)(解析版)
题型:解答题
(2009•漳州)几何模型:
条件:如下图,A、B是直线l同旁的两个定点.

问题:在直线l上确定一点P,使PA+PB的值最小.
方法:作点A关于直线l的对称点A′,连接A′B交l于点P,则PA+PB=A′B的值最小(不必证明).
模型应用:
(1)如图1,正方形ABCD的边长为2,E为AB的中点,P是AC上一动点.连接BD,由正方形对称性可知,B与D关于直线AC对称.连接ED交AC于P,则PB+PE的最小值是______;
(2)如图2,⊙O的半径为2,点A、B、C在⊙O上,OA⊥OB,∠AOC=60°,P是OB上一动点,求PA+PC的最小值;
(3)如图3,∠AOB=45°,P是∠AOB内一点,PO=10,Q、R分别是OA、OB上的动点,求△PQR周长的最小值.
查看答案和解析>>
科目:czsx
来源:2010年福建省莆田市中考数学仿真模拟试卷(二)(解析版)
题型:解答题
(2009•漳州)几何模型:
条件:如下图,A、B是直线l同旁的两个定点.

问题:在直线l上确定一点P,使PA+PB的值最小.
方法:作点A关于直线l的对称点A′,连接A′B交l于点P,则PA+PB=A′B的值最小(不必证明).
模型应用:
(1)如图1,正方形ABCD的边长为2,E为AB的中点,P是AC上一动点.连接BD,由正方形对称性可知,B与D关于直线AC对称.连接ED交AC于P,则PB+PE的最小值是______;
(2)如图2,⊙O的半径为2,点A、B、C在⊙O上,OA⊥OB,∠AOC=60°,P是OB上一动点,求PA+PC的最小值;
(3)如图3,∠AOB=45°,P是∠AOB内一点,PO=10,Q、R分别是OA、OB上的动点,求△PQR周长的最小值.
查看答案和解析>>
科目:czsx
来源:2012年北师大版初三中考数学模拟试卷(三)(解析版)
题型:解答题
几何模型:
条件:如下图,A、B是直线l同旁的两个定点.
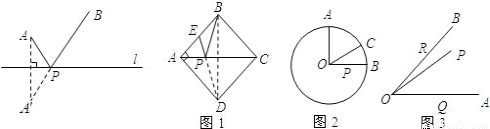
问题:在直线l上确定一点P,使PA+PB的值最小.
方法:作点A关于直线l的对称点A′,连接A′B交l于点P,则PA+PB=A′B的值最小(不必证明).
模型应用:
(1)如图1,正方形ABCD的边长为2,E为AB的中点,P是AC上一动点.连接BD,由正方形对称性可知,B与D关于直线AC对称.连接ED交AC于P,则PB+PE的最小值是______;
(2)如图2,⊙O的半径为2,点A、B、C在⊙O上,OA⊥OB,∠AOC=60°,P是OB上一动点,求PA+PC的最小值;
(3)如图3,∠AOB=45°,P是∠AOB内一点,PO=10,Q、R分别是OA、OB上的动点,求△PQR周长的最小值.
查看答案和解析>>
科目:czsx
来源:2011年浙江省杭州市中考数学模拟试卷(16)(解析版)
题型:解答题
几何模型:
条件:如下图,A、B是直线l同旁的两个定点.

问题:在直线l上确定一点P,使PA+PB的值最小.
方法:作点A关于直线l的对称点A′,连接A′B交l于点P,则PA+PB=A′B的值最小(不必证明).
模型应用:
(1)如图1,正方形ABCD的边长为2,E为AB的中点,P是AC上一动点.连接BD,由正方形对称性可知,B与D关于直线AC对称.连接ED交AC于P,则PB+PE的最小值是______;
(2)如图2,⊙O的半径为2,点A、B、C在⊙O上,OA⊥OB,∠AOC=60°,P是OB上一动点,求PA+PC的最小值;
(3)如图3,∠AOB=45°,P是∠AOB内一点,PO=10,Q、R分别是OA、OB上的动点,求△PQR周长的最小值.
查看答案和解析>>
科目:czsx
来源:2013年四川省成都市中考数学模拟试卷(六)(解析版)
题型:解答题
几何模型:
条件:如下图,A、B是直线l同旁的两个定点.
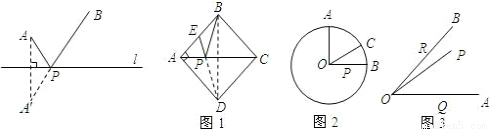
问题:在直线l上确定一点P,使PA+PB的值最小.
方法:作点A关于直线l的对称点A′,连接A′B交l于点P,则PA+PB=A′B的值最小(不必证明).
模型应用:
(1)如图1,正方形ABCD的边长为2,E为AB的中点,P是AC上一动点.连接BD,由正方形对称性可知,B与D关于直线AC对称.连接ED交AC于P,则PB+PE的最小值是______;
(2)如图2,⊙O的半径为2,点A、B、C在⊙O上,OA⊥OB,∠AOC=60°,P是OB上一动点,求PA+PC的最小值;
(3)如图3,∠AOB=45°,P是∠AOB内一点,PO=10,Q、R分别是OA、OB上的动点,求△PQR周长的最小值.
查看答案和解析>>
科目:czsx
来源:2010年河北省石家庄市第28中学中考数学模拟试卷(解析版)
题型:解答题
几何模型:
条件:如下图,A、B是直线l同旁的两个定点.

问题:在直线l上确定一点P,使PA+PB的值最小.
方法:作点A关于直线l的对称点A′,连接A′B交l于点P,则PA+PB=A′B的值最小(不必证明).
模型应用:
(1)如图1,正方形ABCD的边长为2,E为AB的中点,P是AC上一动点.连接BD,由正方形对称性可知,B与D关于直线AC对称.连接ED交AC于P,则PB+PE的最小值是______;
(2)如图2,⊙O的半径为2,点A、B、C在⊙O上,OA⊥OB,∠AOC=60°,P是OB上一动点,求PA+PC的最小值;
(3)如图3,∠AOB=45°,P是∠AOB内一点,PO=10,Q、R分别是OA、OB上的动点,求△PQR周长的最小值.
查看答案和解析>>
科目:czsx
来源:2010年贵州省黔南州惠水县断杉中学中考数学模拟试卷(三)(解析版)
题型:解答题
几何模型:
条件:如下图,A、B是直线l同旁的两个定点.

问题:在直线l上确定一点P,使PA+PB的值最小.
方法:作点A关于直线l的对称点A′,连接A′B交l于点P,则PA+PB=A′B的值最小(不必证明).
模型应用:
(1)如图1,正方形ABCD的边长为2,E为AB的中点,P是AC上一动点.连接BD,由正方形对称性可知,B与D关于直线AC对称.连接ED交AC于P,则PB+PE的最小值是______;
(2)如图2,⊙O的半径为2,点A、B、C在⊙O上,OA⊥OB,∠AOC=60°,P是OB上一动点,求PA+PC的最小值;
(3)如图3,∠AOB=45°,P是∠AOB内一点,PO=10,Q、R分别是OA、OB上的动点,求△PQR周长的最小值.
查看答案和解析>>
科目:czsx
来源:2013年浙江省丽水市中考数学预测试卷(解析版)
题型:解答题
几何模型:
条件:如下图,A、B是直线l同旁的两个定点.
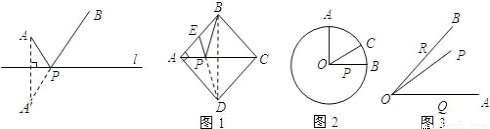
问题:在直线l上确定一点P,使PA+PB的值最小.
方法:作点A关于直线l的对称点A′,连接A′B交l于点P,则PA+PB=A′B的值最小(不必证明).
模型应用:
(1)如图1,正方形ABCD的边长为2,E为AB的中点,P是AC上一动点.连接BD,由正方形对称性可知,B与D关于直线AC对称.连接ED交AC于P,则PB+PE的最小值是______;
(2)如图2,⊙O的半径为2,点A、B、C在⊙O上,OA⊥OB,∠AOC=60°,P是OB上一动点,求PA+PC的最小值;
(3)如图3,∠AOB=45°,P是∠AOB内一点,PO=10,Q、R分别是OA、OB上的动点,求△PQR周长的最小值.
查看答案和解析>>
科目:czsx
来源:2012年湖北省恩施州鹤峰县中考数学一模试卷(解析版)
题型:解答题
几何模型:
条件:如下图,A、B是直线l同旁的两个定点.

问题:在直线l上确定一点P,使PA+PB的值最小.
方法:作点A关于直线l的对称点A′,连接A′B交l于点P,则PA+PB=A′B的值最小(不必证明).
模型应用:
(1)如图1,正方形ABCD的边长为2,E为AB的中点,P是AC上一动点.连接BD,由正方形对称性可知,B与D关于直线AC对称.连接ED交AC于P,则PB+PE的最小值是______;
(2)如图2,⊙O的半径为2,点A、B、C在⊙O上,OA⊥OB,∠AOC=60°,P是OB上一动点,求PA+PC的最小值;
(3)如图3,∠AOB=45°,P是∠AOB内一点,PO=10,Q、R分别是OA、OB上的动点,求△PQR周长的最小值.
查看答案和解析>>
科目:czsx
来源:2012年安徽省中考数学模拟试卷(十六)(解析版)
题型:解答题
几何模型:
条件:如下图,A、B是直线l同旁的两个定点.

问题:在直线l上确定一点P,使PA+PB的值最小.
方法:作点A关于直线l的对称点A′,连接A′B交l于点P,则PA+PB=A′B的值最小(不必证明).
模型应用:
(1)如图1,正方形ABCD的边长为2,E为AB的中点,P是AC上一动点.连接BD,由正方形对称性可知,B与D关于直线AC对称.连接ED交AC于P,则PB+PE的最小值是______;
(2)如图2,⊙O的半径为2,点A、B、C在⊙O上,OA⊥OB,∠AOC=60°,P是OB上一动点,求PA+PC的最小值;
(3)如图3,∠AOB=45°,P是∠AOB内一点,PO=10,Q、R分别是OA、OB上的动点,求△PQR周长的最小值.
查看答案和解析>>
科目:czsx
来源:北京市延庆区2010届初三第一次统一练习数学试卷
题型:044
几何模型:
条件:如下图,
A、B是直线l同旁的两个定点.问题:在直线l上确定一点P,使PA+PB的值最小.

方法:作点
A关于直线l的对称点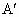 ,连结
,连结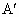 B交l于点P,则PA+PB=
B交l于点P,则PA+PB=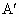 B的值最小
B的值最小(
不必证明)
.
模型应用:
(1)如图,正方形ABCD的边长为2,E为AB的中点,P是AC上一动点.连结BD,由正方形对称性可知,B与D关于直线AC对称.连结ED交AC于P,则PB+PE的最小值是________;
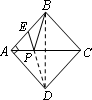
(2)如图,⊙O的半径为2,点A、B、C在⊙O上,OA⊥OB,∠AOC=60°,P是OB上一动点,则PA+PC的最小值是________;
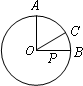
(3)如图,∠AOB=45°,P是∠AOB内一点,PO=10,Q、R分别是OA、OB上
的动点,则△PQR周长的最小值是________.
查看答案和解析>>
科目:czsx
来源:2010年北京市怀柔区中考数学二模试卷(解析版)
题型:解答题
几何模型:
条件:如下图,A、B是直线l同旁的两个定点.

问题:在直线l上确定一点P,使PA+PB的值最小.
方法:作点A关于直线l的对称点A′,连接A′B交l于点P,则PA+PB=A′B的值最小(不必证明).
模型应用:
(1)如图1,正方形ABCD的边长为2,E为AB的中点,P是AC上一动点.连接BD,由正方形对称性可知,B与D关于直线AC对称.连接ED交AC于P,则PB+PE的最小值是______;
(2)如图2,⊙O的半径为2,点A、B、C在⊙O上,OA⊥OB,∠AOC=60°,P是OB上一动点,求PA+PC的最小值;
(3)如图3,∠AOB=45°,P是∠AOB内一点,PO=10,Q、R分别是OA、OB上的动点,求△PQR周长的最小值.
查看答案和解析>>
科目:czsx
来源:2010年江苏省盐城市盐都区中考数学一模试卷(解析版)
题型:解答题
(2009•漳州)几何模型:
条件:如下图,A、B是直线l同旁的两个定点.

问题:在直线l上确定一点P,使PA+PB的值最小.
方法:作点A关于直线l的对称点A′,连接A′B交l于点P,则PA+PB=A′B的值最小(不必证明).
模型应用:
(1)如图1,正方形ABCD的边长为2,E为AB的中点,P是AC上一动点.连接BD,由正方形对称性可知,B与D关于直线AC对称.连接ED交AC于P,则PB+PE的最小值是______;
(2)如图2,⊙O的半径为2,点A、B、C在⊙O上,OA⊥OB,∠AOC=60°,P是OB上一动点,求PA+PC的最小值;
(3)如图3,∠AOB=45°,P是∠AOB内一点,PO=10,Q、R分别是OA、OB上的动点,求△PQR周长的最小值.
查看答案和解析>>

 几何模型:条件:如图,A、B是直线l同旁的两个定点.
几何模型:条件:如图,A、B是直线l同旁的两个定点.
 几何模型:
几何模型:
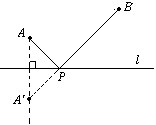


 几何模型:条件:如图,A、B是直线l同旁的两个定点.
几何模型:条件:如图,A、B是直线l同旁的两个定点.
 几何模型:
几何模型: