
科目:czsx 来源: 题型:
 如图,在平面直角坐标系xoy内,点P在直线y=
如图,在平面直角坐标系xoy内,点P在直线y=| 1 |
| 2 |
| 5 |
| k |
| x |
科目:czsx 来源: 题型:
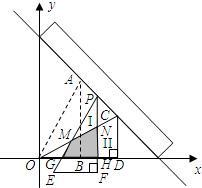 从上方紧靠两纸板放置,让纸板Ⅰ沿直尺边缘平行移动.当纸板Ⅰ移动至△PEF处时,设PE,PF与OC分别交于点M,N,与x轴分别交于点G,H.
从上方紧靠两纸板放置,让纸板Ⅰ沿直尺边缘平行移动.当纸板Ⅰ移动至△PEF处时,设PE,PF与OC分别交于点M,N,与x轴分别交于点G,H.科目:czsx 来源: 题型:
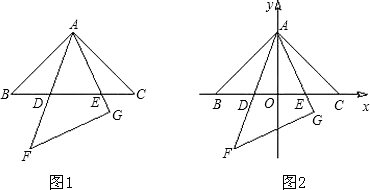
科目:czsx 来源: 题型:
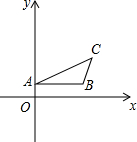
 (2011•道外区二模)点A(6,4)和点B(2,1)在平面直角坐标系中的位置如图所示.
(2011•道外区二模)点A(6,4)和点B(2,1)在平面直角坐标系中的位置如图所示.科目:czsx 来源: 题型:
 如图,在平面直角坐标系中,点A的坐标为(0,1),点B的坐标为(3,1),C的坐标为
如图,在平面直角坐标系中,点A的坐标为(0,1),点B的坐标为(3,1),C的坐标为科目:czsx 来源: 题型:
| 3 |
| 4 |
| A、9个 | B、7个 | C、5个 | D、3个 |
科目:czsx 来源: 题型:
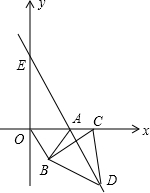 点C为x轴的正半轴上一动点(OC>2),连接BC,以BC为边在第四象限内作等边△CBD,直线DA交y轴于点E.
点C为x轴的正半轴上一动点(OC>2),连接BC,以BC为边在第四象限内作等边△CBD,直线DA交y轴于点E.科目:czsx 来源: 题型:
| 3m-12 |

科目:czsx 来源: 题型:
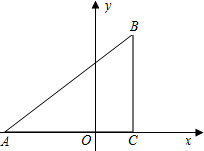 坐标分别为A(-3,0),C(1,0),tan∠BAC=
坐标分别为A(-3,0),C(1,0),tan∠BAC=| 3 | 4 |
科目:czsx 来源: 题型:
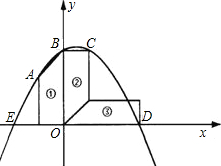 x2-bx-c经过梯形的顶点A、B、C、D,已知梯形的两条底边长分别为4,6.
x2-bx-c经过梯形的顶点A、B、C、D,已知梯形的两条底边长分别为4,6.科目:czsx 来源: 题型:
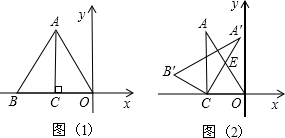
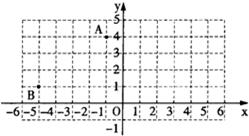 12、点A(-l,4)和点B(-5,1)在平面直角坐标系中的位置如图所示:将点A、B分别向右平移5个单位,得到点A1、B1,画出四边形AA1B1B;并画一条直线,将四边形AA1B1B分成两个全等的图形,并且每个图形都是轴对称图形.
12、点A(-l,4)和点B(-5,1)在平面直角坐标系中的位置如图所示:将点A、B分别向右平移5个单位,得到点A1、B1,画出四边形AA1B1B;并画一条直线,将四边形AA1B1B分成两个全等的图形,并且每个图形都是轴对称图形.科目:czsx 来源: 题型:
| k | x |

科目:czsx 来源: 题型:
| 3 |
科目:czsx 来源: 题型:
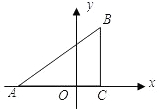 ,C(1,0),tan∠BAC=
,C(1,0),tan∠BAC=| 3 | 4 |
科目:czsx 来源: 题型:
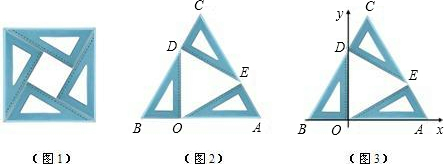
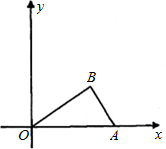
 在平面直角坐标系中,点A(2,0),B(0,4),作△BOC,使△BOC与△ABO全等,则点C坐标为
在平面直角坐标系中,点A(2,0),B(0,4),作△BOC,使△BOC与△ABO全等,则点C坐标为科目:czsx 来源: 题型:
科目:czsx 来源: 题型:
 为
为| 16 | 5 |
科目:czsx 来源: 题型:
| 3 |
| 1 |
| a |
科目:czsx 来源: 题型:
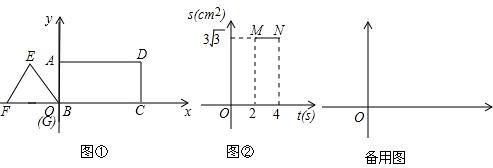
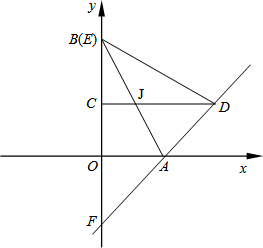 (2013•石景山区一模)如图,把两个全等的Rt△AOB和Rt△ECD分别置于平面直角坐标系xOy中,使点E与点B重合,直角边OB、BC在y轴上.已知点D (4,2),过A、D两点的直线交y轴于点F.若△ECD沿DA方向以每秒
(2013•石景山区一模)如图,把两个全等的Rt△AOB和Rt△ECD分别置于平面直角坐标系xOy中,使点E与点B重合,直角边OB、BC在y轴上.已知点D (4,2),过A、D两点的直线交y轴于点F.若△ECD沿DA方向以每秒| 2 |
科目:czsx 来源: 题型:
 (2013•贵港)如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+c交y轴于点C(0,4),对称轴x=2与x轴交于点D,顶点为M,且DM=OC+OD.
(2013•贵港)如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+c交y轴于点C(0,4),对称轴x=2与x轴交于点D,顶点为M,且DM=OC+OD.