精英家教网 >
试题搜索列表 >在△abc中,∠acb=90°,d是ab上的一点,bd=bc,过点d作ab的垂线交ac与点e,连接be,cd交于点m,求证:cd⊥be
在△abc中,∠acb=90°,d是ab上的一点,bd=bc,过点d作ab的垂线交ac与点e,连接be,cd交于点m,求证:cd⊥be答案解析
科目:czsx
来源:
题型:
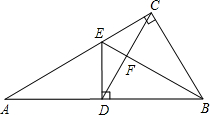
如图,在Rt△ABC中,∠ACB=90°,D是AB上的一点,BD=BC,过点D作AB的垂线交AC于点E,CD交BE于点F.
求证:BE垂直平分CD.
查看答案和解析>>
科目:czsx
来源:
题型:

如图,Rt△ABC中,∠ACB=90°,D是AB上的一点,BD=BC.过D作AB的垂线交AC于点E,CD交BE于点F.求证:BE⊥CD.
查看答案和解析>>
科目:czsx
来源:
题型:

如图,Rt△ABC中,∠ACB=90°,D是AB上的一点,BD=BC.过D作AB的垂线交AC于点E,CD交BE于点F.猜想BE与CD的关系,并证明.
查看答案和解析>>
科目:czsx
来源:重庆市期末题
题型:证明题
如图,Rt△ABC中,∠ACB=90°,D是AB上的一点,BD=BC,过D作AB的垂线交AC于点E,CD交BE于点F。求证:BE⊥CD。
查看答案和解析>>
科目:czsx
来源:重庆市期末题
题型:解答题
如图,Rt△ABC中,∠ACB=90°,D是AB上的一点,BD=BC.过D作AB的垂线交AC于点E,CD交BE于点F.求证:BE⊥CD.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
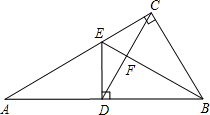 如图,Rt△ABC中,∠ACB=90°,D是AB上的一点,BD=BC.过D作AB的垂线交AC于点E,CD交BE于点F.求证:BE⊥CD.
如图,Rt△ABC中,∠ACB=90°,D是AB上的一点,BD=BC.过D作AB的垂线交AC于点E,CD交BE于点F.求证:BE⊥CD.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
 如图,Rt△ABC中,∠ACB=90°,D是AB上的一点,BD=BC.过D作AB的垂线交AC于点E,CD交BE于点F.猜想BE与CD的关系,并证明.
如图,Rt△ABC中,∠ACB=90°,D是AB上的一点,BD=BC.过D作AB的垂线交AC于点E,CD交BE于点F.猜想BE与CD的关系,并证明.
查看答案和解析>>
科目:czsx
来源:
题型:
如图,Rt△ABC中,∠ACB=900,D是AB上的一点,BD=BC.过D作AB的垂线交AC于点E,CD交BE于点F.求证:BE⊥CD.
查看答案和解析>>
科目:czsx
来源:
题型:

如图,在△ABC中,∠A=90°,D是AC上的一点,BD=DC,P是BC上的任一点,PE⊥BD,PF⊥AC,E、F为垂足.求证:PE+PF=AB.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
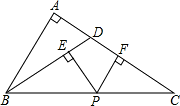 如图,在△ABC中,∠A=90°,D是AC上的一点,BD=DC,P是BC上的任一点,PE⊥BD,PF⊥AC,E、F为垂足.求证:PE+PF=AB.
如图,在△ABC中,∠A=90°,D是AC上的一点,BD=DC,P是BC上的任一点,PE⊥BD,PF⊥AC,E、F为垂足.求证:PE+PF=AB.
查看答案和解析>>
科目:czsx
来源:
题型:

已知:如图,在Rt△ABC中,∠ACB=90°,CD是AB上的中点,过点B作BE⊥CD,垂足为E.
求证:△ABC∽△BCE.
查看答案和解析>>
科目:czsx
来源:
题型:
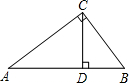
如图,在△ABC中,∠ACB=90°,CD是AB边上的高,∠A=30°,则下列结论中正确的是( )
查看答案和解析>>
科目:czsx
来源:
题型:
已知在Rt△ABC中,∠ACB=90°,CD是AB上的中线,BC=
2,cos∠ACD=
,则CD=
.
查看答案和解析>>
科目:czsx
来源:
题型:

如图,在△ABC中,∠ACB=90°,CD是AB边上的高,且AB=13cm,BC=12cm,AC=5cm.求:
(1)△ABC的面积;
(2)CD的长.
查看答案和解析>>
科目:czsx
来源:
题型:
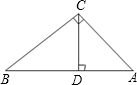
如图,在△ABC中,∠ACB=90°,CD是AB边上的高,AB=5,BC=4,AC=3,
求:(1)△ABC的面积;
(2)CD的长?
查看答案和解析>>
科目:czsx
来源:
题型:
13、已知在△ABC中,∠ACB=90°,CD是AB边上的高,∠B=30°,AD=a,则AB=
4a
.
查看答案和解析>>
科目:czsx
来源:
题型:
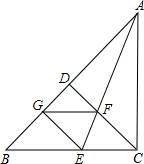
如图,在△ABC中,∠ACB=90°,CD是AB边上的高,∠BAC的平分线AE交CD于F,EG⊥AB于G.
(1)求证:△AEG≌△AEC;
(2)△CEF是否为等腰三角形,请证明你的结论;
(3)四边形GECF是否为菱形,请证明你的结论.
查看答案和解析>>
科目:czsx
来源:
题型:
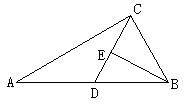
24、如图,在Rt△ABC中,∠ACB=90°,D是AB边上的一点,DC的中垂线EB经过点B,AC=4,AD=2.
①求证:∠CBE=∠DBE;
②求BC的长.
查看答案和解析>>
科目:czsx
来源:
题型:
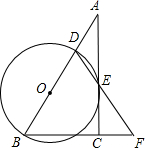
(2013•宁夏)在Rt△ABC中,∠ACB=90°,D是AB边上的一点,以BD为直径作⊙O交AC于点E,连结DE并延长,与BC的延长线交于点F.且BD=BF.
(1)求证:AC与⊙O相切.
(2)若BC=6,AB=12,求⊙O的面积.
查看答案和解析>>
科目:czsx
来源:
题型:

20、如图,在△ABC中,∠ACB=90°,CD是AB边上的高,∠A=30°.求证:AB=4BD.
查看答案和解析>>

 如图,Rt△ABC中,∠ACB=90°,D是AB上的一点,BD=BC.过D作AB的垂线交AC于点E,CD交BE于点F.猜想BE与CD的关系,并证明.
如图,Rt△ABC中,∠ACB=90°,D是AB上的一点,BD=BC.过D作AB的垂线交AC于点E,CD交BE于点F.猜想BE与CD的关系,并证明.

 如图,Rt△ABC中,∠ACB=90°,D是AB上的一点,BD=BC.过D作AB的垂线交AC于点E,CD交BE于点F.猜想BE与CD的关系,并证明.
如图,Rt△ABC中,∠ACB=90°,D是AB上的一点,BD=BC.过D作AB的垂线交AC于点E,CD交BE于点F.猜想BE与CD的关系,并证明. 如图,在△ABC中,∠A=90°,D是AC上的一点,BD=DC,P是BC上的任一点,PE⊥BD,PF⊥AC,E、F为垂足.求证:PE+PF=AB.
如图,在△ABC中,∠A=90°,D是AC上的一点,BD=DC,P是BC上的任一点,PE⊥BD,PF⊥AC,E、F为垂足.求证:PE+PF=AB. 如图,在△ABC中,∠ACB=90°,CD是AB边上的高,且AB=13cm,BC=12cm,AC=5cm.求:
如图,在△ABC中,∠ACB=90°,CD是AB边上的高,且AB=13cm,BC=12cm,AC=5cm.求: 如图,在△ABC中,∠ACB=90°,CD是AB边上的高,∠BAC的平分线AE交CD于F,EG⊥AB于G.
如图,在△ABC中,∠ACB=90°,CD是AB边上的高,∠BAC的平分线AE交CD于F,EG⊥AB于G. 24、如图,在Rt△ABC中,∠ACB=90°,D是AB边上的一点,DC的中垂线EB经过点B,AC=4,AD=2.
24、如图,在Rt△ABC中,∠ACB=90°,D是AB边上的一点,DC的中垂线EB经过点B,AC=4,AD=2.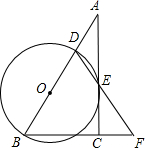 (2013•宁夏)在Rt△ABC中,∠ACB=90°,D是AB边上的一点,以BD为直径作⊙O交AC于点E,连结DE并延长,与BC的延长线交于点F.且BD=BF.
(2013•宁夏)在Rt△ABC中,∠ACB=90°,D是AB边上的一点,以BD为直径作⊙O交AC于点E,连结DE并延长,与BC的延长线交于点F.且BD=BF.