科目：czsx 来源： 题型：
10、如图所示在三角形△ABC中AB=AC，AD是△ABC的角平分线，DE⊥AB，DF⊥AC，垂足分别为E、F，则下列四个结论中，①AB上一点与AC上一点到D的距离相等；②AD上任意一点到AB、AC的距离相等；③∠BDE=∠CDF；④BD=CD，AD⊥BC．其中正确的个数是（ ）科目：czsx 来源：2015届湖北罗田石桥铺中学八年级上学期期中考试数学试卷（解析版） 题型：选择题
如图,在三角形ABC中,∠C=90,AC=4cm,AB=7cm,AD平分∠BAC交BC于点D，DE⊥AB于点E，则EB的长是：（ ）
A．3cm, B.4cm C.5cm D.不能确定
科目：czsx 来源：2015届湖北罗田石桥铺中学八年级上学期期中考试数学试卷（解析版） 题型：选择题
如图,在三角形ABC中,∠C=90,AC=4cm,AB=7cm,AD平分∠BAC交BC于点D，DE⊥AB于点E，则EB的长是：（ ）
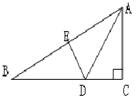
A．3cm, B.4cm C.5cm D.不能确定
科目：czsx 来源：2015届湖北罗田石桥铺中学八年级上学期期中考试数学试卷（解析版） 题型：选择题
如图,在三角形ABC中,∠C=90,AC=4cm,AB=7cm,AD平分∠BAC交BC于点D，DE⊥AB于点E，则EB的长是：（ ）
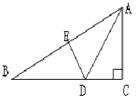
A．3cm, B.4cm C.5cm D.不能确定
科目：czsx 来源：2015届湖北罗田石桥铺中学八年级上学期期中考试数学试卷（解析版） 题型：选择题
如图,在三角形ABC中,∠C=90,AC=4cm,AB=7cm,AD平分∠BAC交BC于点D，DE⊥AB于点E，则EB的长是：（ ）
A．3cm, B.4cm C.5cm D.不能确定
科目：czsx 来源：2015届湖北罗田石桥铺中学八年级上学期期中考试数学试卷（解析版） 题型：选择题
如图,在三角形ABC中,∠C=90,AC=4cm,AB=7cm,AD平分∠BAC交BC于点D，DE⊥AB于点E，则EB的长是：（ ）
A．3cm, B.4cm C.5cm D.不能确定
科目：czsx 来源：2015届湖北罗田石桥铺中学八年级上学期期中考试数学试卷（解析版） 题型：选择题
如图,在三角形ABC中,∠C=90,AC=4cm,AB=7cm,AD平分∠BAC交BC于点D，DE⊥AB于点E，则EB的长是：（ ）
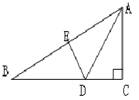
A．3cm, B.4cm C.5cm D.不能确定
科目：czsx 来源：2015届湖北罗田石桥铺中学八年级上学期期中考试数学试卷（解析版） 题型：选择题
如图,在三角形ABC中,∠C=90,AC=4cm,AB=7cm,AD平分∠BAC交BC于点D，DE⊥AB于点E，则EB的长是：（ ）
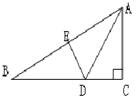
A．3cm, B.4cm C.5cm D.不能确定
科目：czsx 来源：2015届湖北罗田石桥铺中学八年级上学期期中考试数学试卷（解析版） 题型：选择题
如图,在三角形ABC中,∠C=90,AC=4cm,AB=7cm,AD平分∠BAC交BC于点D，DE⊥AB于点E，则EB的长是：（ ）
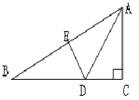
A．3cm, B.4cm C.5cm D.不能确定
科目：czsx 来源：2015届湖北罗田石桥铺中学八年级上学期期中考试数学试卷（解析版） 题型：选择题
如图,在三角形ABC中,∠C=90,AC=4cm,AB=7cm,AD平分∠BAC交BC于点D，DE⊥AB于点E，则EB的长是：（ ）
A．3cm, B.4cm C.5cm D.不能确定
科目：czsx 来源：2015届湖北罗田石桥铺中学八年级上学期期中考试数学试卷（解析版） 题型：选择题
如图,在三角形ABC中,∠C=90,AC=4cm,AB=7cm,AD平分∠BAC交BC于点D，DE⊥AB于点E，则EB的长是：（ ）
A．3cm, B.4cm C.5cm D.不能确定
科目：czsx 来源：不详 题型：单选题
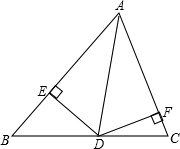
| A．1个 | B．2个 | C．3个 | D．4个 |
科目：czsx 来源： 题型：单选题
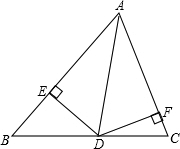如图所示在三角形△ABC中AB=AC，AD是△ABC的角平分线，DE⊥AB，DF⊥AC，垂足分别为E、F，则下列四个结论中，①AB上有一点与AC上一点到D的距离相等；②AD上任意一点到AB、AC的距离相等；③∠BDE=∠CDF；④BD=CD，AD⊥BC．其中正确的个数是科目：czsx 来源： 题型：
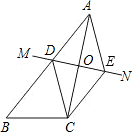如图，三角形ABC中，AC的垂直平分线MN交AB于点D，交AC于点O，CE∥AB交MN于E连结AE、CD．科目：czsx 来源： 题型：
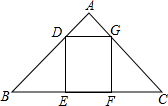（2013•嘉定区一模）如图已知△ABC中AB=AC=10，BC=16，矩形DEFG的边EF在△ABC的边BC上，顶点D、G分别在AB、AC上，设DE的长为x，矩形DEFG的面积为y，求y关于x的函数关系式，并写出这个函数的定义域．科目：czsx 来源：2012年初中毕业升学考试（上海卷）数学（带解析） 题型：解答题
如图在Rt△ABC中，∠ACB=90°，D是边AB的中点，BE⊥CD，垂足为点E．已知AC=15，cosA=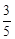
．
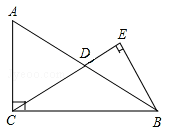
（1）求线段CD的长；
（2）求sin∠DBE的值．
科目：czsx 来源： 题型：解答题
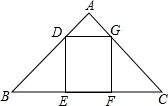如图已知△ABC中AB=AC=10，BC=16，矩形DEFG的边EF在△ABC的边BC上，顶点D、G分别在AB、AC上，设DE的长为x，矩形DEFG的面积为y，求y关于x的函数关系式，并写出这个函数的定义域．科目：czsx 来源： 题型：
如图8-23,△ABC中,AB=AC,D、E、F分别为AB、BC、CA上的点,且BD=CE,∠DEF=∠B.
图8-23
(1)请指出图中的等腰三角形为______________(除△ABC外).
(2)其中哪两条线段相等?请说明.
科目：czsx 来源： 题型：
如图8-15,在Rt△ABC中,AB=AC,∠BAC=90°,O为BC中点.
图8-15
(1)写出O点到△ABC三个顶点A、B、C的距离关系(不要求证明);
(2)如果M、N分别在线段AB、AC上移动,在移动过程中保持AN=BM,请判断△OMN的形状,并证明你的结论.