精英家教网 >
试题搜索列表 >表中已经填2、0、1、2四个数,每行中右边数减去左边数都相等,每列中下边数减去上边数也都相等,那么这表中16个数的总和是 .
表中已经填2、0、1、2四个数,每行中右边数减去左边数都相等,每列中下边数减去上边数也都相等,那么这表中16个数的总和是 .答案解析
科目:czsx
来源:
题型:填空题
 表中已经填2、0、1、2四个数,每行中右边数减去左边数都相等,每列中下边数减去上边数也都相等,那么这表中16个数的总和是________.
表中已经填2、0、1、2四个数,每行中右边数减去左边数都相等,每列中下边数减去上边数也都相等,那么这表中16个数的总和是________.
查看答案和解析>>
科目:czsx
来源:
题型:
(2013•德州)设A是由2×4个整数组成的2行4列的数表,如果某一行(或某一列)各数之和为负数,则改变该行(或该列)中所有数的符号,称为一次“操作”.
(1)数表A如表1所示,如果经过两次“操作”,使得到的数表每行的各数之和与每列的各数之和均为非负整数,请写出每次“操作”后所得的数表;(写出一种方法即可)
表1
(2)数表A如表2所示,若经过任意一次“操作”以后,便可使得到的数表每行的各数之和与每列的各数之和均为非负整数,求整数a的值
表2.
| a |
a2-1 |
-a |
-a2 |
| 2-a |
1-a2 |
a-2 |
a2 |
查看答案和解析>>
科目:czsx
来源:
题型:
图1是一个3×3方阵图,每行的三个数、每列的三个数,每斜对角的三个数相加的和均相等.
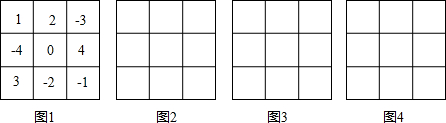
如何把9个连续整数迅速填入一个3×3方阵,使每行、每列、每斜对角的三个数相加的和均相等,是我们祖先早就在研究的问题.古代的“洛书”、汉朝徐岳的“九宫算”就揭示出祖先们得到的神奇填写方法.图1显示出把-4,-3,-2,-1,0,1,2,3,4填入一个3×3方阵,使每行、每列、每斜对角的三个数相加的和均相等的一种方法.同学们,你能正确填写吗?马上试一试:
(1)请观察图1中数字的填写规律,然后将下列各数组中的9个数分别填入图2、图3、图4所示的9个空格中,使得每行的三个数、每列的三个数,每斜对角的三个数相加的和均相等;
①6,5,4,3,2,1,0,-1,-2
②9,8,7,6,5,4,3,2,1
③-8,-6,-4,-2,0,2,4,6,8
(2)拓展探究:在图5所示 9个空格中,填入5个2和4个-2,使得每行、每列、每斜对角的三个数的乘积都是8;
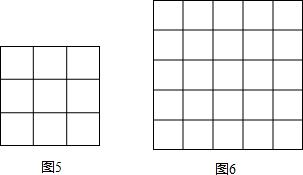
(3)拓展再探究:将25,24,23,22,21,20,19,18,17,16,15,14,13,12,11,10,9,8,7,6,5,4,3,2,1这25个数分别填入图 6所示25个空格中,使得每行、每列、每斜对角的五个数相加的和均相等.
查看答案和解析>>
科目:czsx
来源:
题型:阅读理解
在数学文化节第一轮活动中,我们以探讨一个趣题的方式纪念了数学大师欧拉诞辰300周年.著名数学家拉普拉斯说过:“读读欧拉,他是我们所有人的导师.”是啊!欧拉在数学上的贡献实在太多了,即使在初等数学中也到处可见他的身影.我们再来看看欧拉研究过的“36军官问题”:
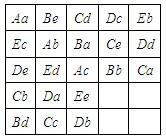
从6支部队中各选出6名不同军衔的军官,将这36名军官排成一个6行6列的方阵,要求每行每列的6个军官分别来自不同的部队,并具有不同的军衔.用大写字母A,B,C,D,E,F分别表示6支不同的部队,用小写字母a,b,c,d,e,f分别表示6种不同的军衔,于是问题转化为:在6×6的方格阵中,每个方格分别填入一个大写字母和一个小写字母,使每行和每列中的大小写字母只能各出现一次(通常称这种方阵为欧拉方阵或正交拉丁方).欧拉搅尽脑汁,也没能排出符合要求的6×6方阵,他猜想并不存在这样的6×6方阵.100多年以后,才有人证明了欧拉的这个猜想是正确的.
于是欧拉继而探究了其他情形,例如,他分别作出了3×3,4×4,5×5正交拉丁方,并证明了当n除以4的余数不等于2时,n×n正交拉丁方是存在的.
正交拉丁方在药品配方试验设计等方面有着广泛应用.现在流行的“数独”游戏和比赛,就是发源于拉丁方问题呢!
如图是一个5×5正交拉丁方,请将剩余的字母填上
.
查看答案和解析>>
科目:czsx
来源:
题型:

把绝对值小于5的整数分别填入下图的各个方格中(每数只能用一次),使得每行、每列以及对角线上的数字之和都相等.
查看答案和解析>>
科目:czsx
来源:
题型:
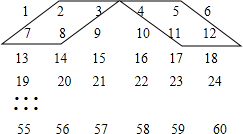
将正整数1~60排成如数表:
用如图的平行四边形在数表中框出四个数,设最小的数为a,
(1)如图表中形如左边的平行四边形框,则另外的三个数分别为
a+1
a+1
,
a+5
a+5
,
a+6
a+6
;如图表中形如右边的平行四边形框,则另外的三个数分别为
a+1
a+1
,
a+7
a+7
,
a+8
a+8
;
(2)能否让图中的平行四边形框出的四个数之和为100吗?如果能,请求出最小的数a,如果不能,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
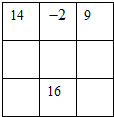
数学游戏题
(1)如图是一个三阶幻方,有9个数字构成,并且每横行,竖行和对角线上的3个数字的和都相等,试填出空格中的数.
(2)有一种“二十四点”的游戏(即算24游戏),其游戏规则是这样的:任取四个1至13之间的自然数,将这四个数(每个数用且只能用一次)进行加减乘除四则运算,使其结果等于24.例如对1,2,3,4,可作如下运算:(1+2+3)×4=24(上述运算与4×(1+2+3)视为相同方法的运算)
①给出有理数4,6,9,12;请你写出一个算式使其结果为24.
②在我们学过负数以后这个游戏仍可以玩,如-2,-3,4,5可以列出算式-2×(-3-4-5)=24;现给出3,-5,6,-8四个数,请你写出一个算式使其结果为24.
查看答案和解析>>
科目:czsx
来源:2013年初中毕业升学考试(山东德州卷)数学(解析版)
题型:解答题
设A是由2×4个整数组成的2行4列的数表,如果某一行(或某一列)各数之和为负数,则改变该行(或该列)中所有数的符号,称为一次“操作”.
(1)数表A如表1所示,如果经过两次“操作”,使得到的数表每行的各数之和与每列的各数之和均为非负整数,请写出每次“操作”后所得的数表;(写出一种方法即可)
表1.
(2)数表A如表2所示,若经过任意一次“操作”以后,便可使得到的数表每行的各数之和与每列的各数之和均为非负整数,求整数a的值
表2.
|
a
|
a2﹣1
|
﹣a
|
﹣a2
|
|
2﹣a
|
1﹣a2
|
a﹣2
|
a2
|
查看答案和解析>>
科目:czsx
来源:2012-2013学年江苏省张家港市初一第一学期调研数学试卷(带解析)
题型:解答题
查看答案和解析>>
科目:czsx
来源:2015届江苏省张家港市初一第一学期调研数学试卷(解析版)
题型:解答题
数学游戏题:
(1)下图是一个三阶幻方,有9个数字构成,并且每横行,竖行和对角线上的3个数字的和都相等,试填出空格中的数;

(2)有一种“二十四点”的游戏(即算24游戏),其游戏规则是这样的:任取四个1至13之间的自然数,将这四个数(每个数用且只能用一次)进行加减乘除四则运算,使其结果等于24.例如对1,2,3,4,可作如下运算:(1+2+3)×4=24(上述运算与4×(1+2+3)视为相同方法的运算)
①给出有理数4,6,9,12 ;请你写出一个算式使其结果为24;
②在我们学过负数以后这个游戏仍可以玩,如 可以列出算式
可以列出算式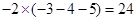 ;现给出
;现给出 四个数,请你写出一个算式使其结果为24.
四个数,请你写出一个算式使其结果为24.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
 将正整数1~60排成如数表:
将正整数1~60排成如数表:
用如图的平行四边形在数表中框出四个数,设最小的数为a,
(1)如图表中形如左边的平行四边形框,则另外的三个数分别为______,______,______;如图表中形如右边的平行四边形框,则另外的三个数分别为______,______,______;
(2)能否让图中的平行四边形框出的四个数之和为100吗?如果能,请求出最小的数a,如果不能,请说明理由.
查看答案和解析>>
科目:czsx
来源:不详
题型:解答题
将正整数1~60排成如数表:
用如图的平行四边形在数表中框出四个数,设最小的数为a,
(1)如图表中形如左边的平行四边形框,则另外的三个数分别为______,______,______;如图表中形如右边的平行四边形框,则另外的三个数分别为______,______,______;
(2)能否让图中的平行四边形框出的四个数之和为100吗?如果能,请求出最小的数a,如果不能,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
设A是由2×4个整数组成的2行4列的数表,如果某一行(或某一列)各数之和为负数,则改变该行(或该列)中所有数的符号,称为一次“操作”.
(1)数表A如表1所示,如果经过两次“操作”,使得到的数表每行的各数之和与每列的各数之和均为非负整数,请写出每次“操作”后所得的数表;(写出一种方法即可)
表1
(2)数表A如表2所示,若经过任意一次“操作”以后,便可使得到的数表每行的各数之和与每列的各数之和均为非负整数,求整数a的值
表2.
| a | a2﹣1 | ﹣a | ﹣a2 |
| 2﹣a | 1﹣a2 | a﹣2 | a2 |
查看答案和解析>>
科目:czsx
来源:活学巧练七年级数学(上)
题型:044
在如图所示的方格中,填入5,6,7,8,9,10,11,12,13这9个数,每行、每列及对角线上各数的和都相等.

查看答案和解析>>
科目:czsx
来源:
题型:解答题
设A是由2×4个整数组成的2行4列的数表,如果某一行(或某一列)各数之和为负数,则改变该行(或该列)中所有数的符号,称为一次“操作”.
(1)数表A如表1所示,如果经过两次“操作”,使得到的数表每行的各数之和与每列的各数之和均为非负整数,请写出每次“操作”后所得的数表;(写出一种方法即可)
表1
(2)数表A如表2所示,若经过任意一次“操作”以后,便可使得到的数表每行的各数之和与每列的各数之和均为非负整数,求整数a的值
表2.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
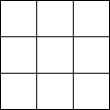 把绝对值小于5的整数分别填入下图的各个方格中(每数只能用一次),使得每行、每列以及对角线上的数字之和都相等.
把绝对值小于5的整数分别填入下图的各个方格中(每数只能用一次),使得每行、每列以及对角线上的数字之和都相等.
查看答案和解析>>
科目:czsx
来源:2013年山东省德州市高级中等学校招生考试数学
题型:044
设A是由2×4个整数组成的2行4列的数表,如果某一行(或某一列)各数之和为负数,则改变该行(或该列)中所有数的符号,称为一次“操作”.
(1)数表A如表1所示,如果经过两次“操作”,使得到的数表每行的各数之和与每列的各数之和均为非负整数,请写出每次“操作”后所得的数表;(写出一种方法即可)
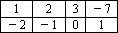
(2)数表A如表所示,若经过任意一次“操作”以后,便可使得到的数表每行的各数之和与每列的各数之和均为非负整数,求整数a的值

查看答案和解析>>
科目:czsx
来源:
题型:解答题
 数学游戏题
数学游戏题
(1)如图是一个三阶幻方,有9个数字构成,并且每横行,竖行和对角线上的3个数字的和都相等,试填出空格中的数.
(2)有一种“二十四点”的游戏(即算24游戏),其游戏规则是这样的:任取四个1至13之间的自然数,将这四个数(每个数用且只能用一次)进行加减乘除四则运算,使其结果等于24.例如对1,2,3,4,可作如下运算:(1+2+3)×4=24(上述运算与4×(1+2+3)视为相同方法的运算)
①给出有理数4,6,9,12;请你写出一个算式使其结果为24.
②在我们学过负数以后这个游戏仍可以玩,如-2,-3,4,5可以列出算式-2×(-3-4-5)=24;现给出3,-5,6,-8四个数,请你写出一个算式使其结果为24.
查看答案和解析>>
科目:czsx
来源:重庆市期末题
题型:探究题
图1是一个3×3方阵图,每行的三个数、每列的三个数,每斜对角的三个数相加的和均相等.如何把9个连续整数迅速填入一个3×3方阵,使每行、每列、每斜对角的三个数相加的和均相等,是我们祖先早就在研究的问题.古代的“洛书”、汉朝徐岳的“九宫算”就揭示出祖先们得到的神奇填写方法.图1显示出把﹣4,﹣3,﹣2,﹣1,0,1,2,3,4填入一个3×3方阵,使每行、每列、每斜对角的三个数相加的和均相等的一种方法.同学们,你能正确填写吗?马上试一试:
(1)请观察图1中数字的填写规律,然后将下列各数组中的9个数分别填入图2、图3、图4所示的9个空格中,使得每行的三个数、每列的三个数,每斜对角的三个数相加的和均相等;
①6,5,4,3,2,1,0,﹣1,﹣2
②9,8,7,6,5,4,3,2,1
③﹣8,﹣6,﹣4,﹣2,0,2,4,6,8
(2)拓展探究:在图5所示 9个空格中,填入5个2和4个﹣2,使得每行、每列、每斜对角的三个数的乘积都是8;
(3)拓展再探究:将25,24,23,22,21,20,19,18,17,16,15,14,13,12,11,10,9,8,7,6,5,4,3,2,1这25个数分别填入图 6所示25个空格中,使得每行、每列、每斜对角的五个数相加的和均相等.
查看答案和解析>>
科目:czsx
来源:2013年山东省济南市中考数学模拟试卷(解析版)
题型:解答题
设A是由2×4个整数组成的2行4列的数表,如果某一行(或某一列)各数之和为负数,则改变该行(或该列)中所有数的符号,称为一次“操作”.
(1)数表A如表1所示,如果经过两次“操作”,使得到的数表每行的各数之和与每列的各数之和均为非负整数,请写出每次“操作”后所得的数表;(写出一种方法即可)
表1
(2)数表A如表2所示,若经过任意一次“操作”以后,便可使得到的数表每行的各数之和与每列的各数之和均为非负整数,求整数a的值
表2.
查看答案和解析>>






 将正整数1~60排成如数表:
将正整数1~60排成如数表: 数学游戏题
数学游戏题
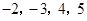 可以列出算式
可以列出算式 ;现给出
;现给出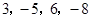 四个数,请你写出一个算式使其结果为24.
四个数,请你写出一个算式使其结果为24.
 可以列出算式
可以列出算式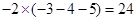 ;现给出
;现给出 四个数,请你写出一个算式使其结果为24.
四个数,请你写出一个算式使其结果为24. 将正整数1~60排成如数表:
将正整数1~60排成如数表: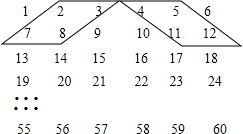
![]()
 数学游戏题
数学游戏题