如图，在两面成“八”字形放置的镜子中间放答案解析

科目：czsx 来源：同步题 题型：解答题

如图，在两面成“八”字形放置的镜子中间放着塑料做的数字9，你在左右两面镜子中看到的像是怎么样的？请你把它们写出来。

科目：czsx 来源：单科王牌　　九年级数学(上) 题型：044

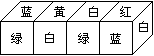
把正方体的六个面上分别涂上不同的颜色，并标上数字，各面上的颜色和数字的对应情况如下表，现将与上述大小相同，颜色与对应数字也完全相同的四个小正方体如图所示拼成一个平面放置的长方体，求此时长方体的下底面的数字和．

科目：czsx 来源： 题型：

如图，在离地面高度6米的C处引拉线固定电线杆，拉线和地面成61°角，求拉线AC的下端A与杆底D的距离AD=

 

米．（精确到0.01米）

科目：czsx 来源： 题型：

如图，在一个坡角为40°的斜坡上有一棵树BC，树高4米．当太阳光AC与水平线成70°角时，该树在斜坡上的树影恰好为线段AB，求树影AB的长．（结果保留一位小数）
（参考数据：sin20°=0.34，tan20°=0.36，sin30°=0.50，tan30°=0.58，sin40°=0.64，tan40°=0.84，sin70°=0.94，tan70°=2.75）

科目：czsx 来源： 题型：

如图，在一个坡角为30°的斜坡上有一棵树，高AB，当太阳光与水平线成60°时，测得该树在斜坡上的树影BC的长为6m，则树高AB=

 

m．

科目：czsx 来源： 题型：

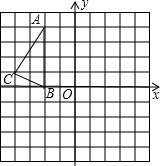（2012•海南）如图，在正方形网格中，△ABC的三个顶点都在格点上，点A、B、C的坐标分别为（-2，4）、（-2，0）、（-4，1），结合所给的平面直角坐标系解答下列问题：
（1）画出△ABC关于原点O对称的△A₁B₁C₁；
（2）平移△ABC，使点A移到点A₂（0，2），画出平移后△A₂B₂C₂并写出点B₂、C₂的坐标；
（3）在△ABC、△A₁B₁C₁、△A₂B₂C₂中，△A₂B₂C₂与

△A₁B₁C₁

△A₁B₁C₁

成中心对称，其对称中心坐标为

（1，-1）

（1，-1）

．

科目：czsx 来源： 题型：

如图，在两面墙之间有一个底端在A点的梯子，当它靠在一侧墙上时，梯子的顶端在B点；当它靠在另一侧墙上时，梯子的顶端在D点．已知∠BAC=60°，∠DAE=45°，点D到地面的垂直距离DE=3

2

m．则点B到地面的垂直距离BC是

3

3

m

3

3

m

．

科目：czsx 来源： 题型：

如图，在针孔成像问题中，根据图形尺寸可知像A′B′的长是物AB长的（　　）

A．3倍

B．不知AB的长度，无法计算

C． 1 3

D． 1 2

科目：czsx 来源： 题型：

28、如图，在离地面高度6米的C处引拉线固定电线杆，拉线和地面成61°角，求拉线AC的长以及拉线下端点A与杆底D的距离AD．（精确到0.01米）

科目：czsx 来源： 题型：

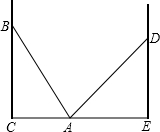如图，在两面墙之间有一个底端在A点的梯子，当它靠在一侧的墙上时，梯子的顶端在B点，当它靠在另一侧的墙上时，梯子的顶端在D点，已知∠BAC=60°，∠DAE=45°，点B到地的垂直距离BC=5

3

米，求两堵墙之间的距离CE．

科目：czsx 来源： 题型：

如图，在由六个全等的正三角形拼成的图中，等腰梯形的个数为（　　）

A．3

B．4

C．5

D．6

科目：czsx 来源： 题型：

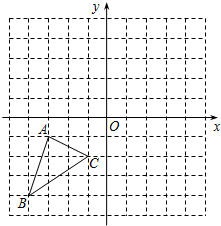19、如图，在正方形网格中，△ABC的三个顶点都在格点上，结合所给的平面直角坐标系解答下列问题：
（1）将△ABC向右平移5个单位长度，画出平移后的△A₁B₁C₁；
（2）画出△ABC关于x轴对称的△A₂B₂C₂；
（3）将△ABC绕原点O旋转180°，画出旋转后的△A₃B₃C₃；
（4）在△A₁B₁C₁、△A₂B₂C₂、△A₃B₃C₃中，△

△A₂B₂C₂

与△

△A₃B₃C₃

成轴对称；△

△A₁B₁C₁

与△

△A₃B₃C₃

成中心对称．

科目：czsx 来源： 题型：

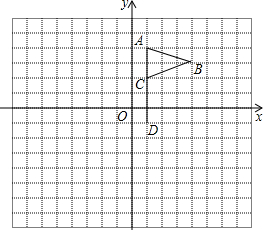如图，在平面直角坐标系中放置着一个小旗ABCD，其四个顶点的坐标分别A（1，4），B（4，3），C（1，2），D（1，-1）．
（1）画出将小旗绕点D逆时针旋转90°得到的图形A₁B₁C₁D；
（2）画出图形A₁B₁C₁D关于原点O成中心对称的图象A₂B₂C₂D₂；
（3）点B₂的坐标为

（3，-2）

（3，-2）

．

科目：czsx 来源： 题型：

20、如图，在一个坡角为20°的斜坡上有一棵树，高为AB，当太阳光线与水平线成52°角时，测得该树斜坡上的树影BC的长为10m，求树高AB（精确到0.1m）
（已知：sin20°≈0.342，cos20°≈0.940，tan20°≈0.364，sin52°≈0.788，cos52°≈0.616，tan52°≈1.280．供选用）

科目：czsx 来源： 题型：阅读理解

（2007•海淀区一模）阅读：
如图，在空间中，与定点的距离等于定长的点的集合叫做球面．定点叫做球心，定长叫做半径．球面被经过球心的平面截得的圆叫做大圆．
探究1：当我们把半径为11cm的足球看成一个球时，假设有一根无弹性的细线恰好能沿足球的大圆紧紧缠绕一周，将细线的长度增加1米后，细线仍以圆形呈现，且圆心为足球的球心．若将细线与足球表面的间隙记为h₁（间隙如图所示），求h₁的长；（π取3.14，结果精确到1cm）
探究2：将探究1中的足球分别换成乒乓球和地球，其他条件都不改变．设乒乓球半径为r，细线与乒乓球表面的间隙为h₂；地球的半径为R，细线与地球表面的间隙为h₃，试比较h₂与h₃大小，并说明理由．

科目：czsx 来源： 题型：

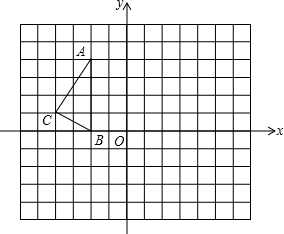如图，在正方形网络中，△ABC的三个顶点都在格点上，点A、B、C的坐标分别为（-2，4）、（-2，0）、（-4，1），结合所给的平面直角坐标系解答下列问题：
（1）画出△ABC关于原点O对称的△A₁B₁C₁；
（2）平移△ABC，使点A移动到点A₂（0，2），画出平移后的△A₂B₂C₂并写出点B₂、C₂的坐标；
（3）△A₁B₁C₁与△A₂B₂C₂成中心对称，写出其对称中心的坐标．

科目：czsx 来源： 题型：

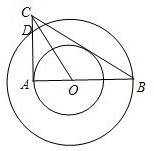22、如图，在以点O为圆心的两个同心圆中，AB经过圆心O，且与小圆相交于A，与大圆相交于点B，小圆的切线AC与大圆相交于D，OC平分∠ACB．
（1）证明直线BC是小圆的切线；
（2）试证明：AC+AD=BC；
（3）若AB=8cm，BC=10cm，求大圆与小圆形成的圆环的面积．

科目：czsx 来源： 题型：

23、如图，在离地面高度6米的C处引拉线固定电线杆，拉线和地面成61°角，求拉线AC的长（精确到0.01米）．

科目：czsx 来源： 题型：

如图，在两面墙之间有一根底端在A点的竹竿，当它靠在一侧墙上时，竹竿的顶端在B点；当它靠在另一侧墙上时，竹竿的顶端在D点．已知∠BAC=60°，∠DAE=45°，AC=2米，则DE的高度为

2

2

2

2

 米．（墙面垂直地面）

科目：czsx 来源： 题型：

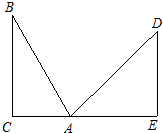如图，在两面墙之间有一个底端在A点的梯子，当它靠在一侧墙上时，梯子的顶端在B点；当它靠在另一侧墙上时，梯子的顶端在D点．已知∠BAC=60°，∠DAE=45°，当D到地面的垂直距离DE=2

2

m，求点B到地面的垂直距离BC（结果保留根号）