如图是规格为8×8的正方形网格,请在所给网格中按下列答案解析
科目:czsx
来源:
题型:
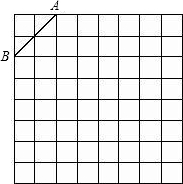
如图是规格为8×8的正方形网格,请在所给网格中按下列要求操作:
(1)请在网格中建立平面直角坐标系,使A点坐标为(-2,4),B点坐标为(-4,2);
(2)在第二象限内的格点上画一点C,使点C与线段AB组成一个以AB为底的等腰三角形,且腰长是无理数,则C点坐标是
,△ABC的周长是
(结果保留根号);
(3)画出△ABC以点C为旋转中心,旋转180°后的△A′B′C,连接AB′和A′B,试说出四边形ABA′B′是何特殊四边形,并说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
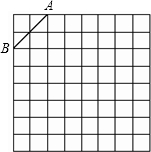
如图是规格为8×8的正方形网格,请在所给网格中按下列要求操作:
在网格中建立平面直角坐标系,以O点为坐标原点,使A点坐标为(-3,5),B点坐标为(-5,3).
(1)C点坐标为(-2,0),则△ABC是
三角形;
(2)在第二象限内的格点上找点P,使点P与线段AB组成等腰三角形,且腰长是无理数,写出所有符合条件的P点坐标
.
查看答案和解析>>
科目:czsx
来源:
题型:
如图是规格为8×8的正方形网格(网格小正方形的边长为1),请在所给网格中按下列要求

操作:
(1)请在网格中建立平面直角坐标系,使A点坐标为(-2,3),B点坐标为(-4,1);
(2)在第二象限内的格点上画一点C,使点C与线段AB围成一个直角三角形(不是等腰直角三角形),则C点坐标是
,△ABC的面积是
;
(3)将(2)中画出△ABC以点C为旋转中心,逆时针旋转90°后得△A′B′C.求经过B、C、B′三点的抛物线的解析式;并判断抛物线是否经过8×8正方形网格的格点(不包括点B、C、B′),若经过,请你直接写出点坐标.
查看答案和解析>>
科目:czsx
来源:
题型:
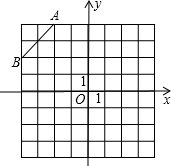
如图是规格为8×8的正方形网格,请在网格中按下列要求操作:
(1)在第二象限内的格点上画一点C,使点C与线段AB组成一个以AB为底的等腰三角形,且腰长是无理数,并求出腰长;
(2)画出△ABC绕点C旋转180°后得到的△A′B′C;连接AB′和A′B,试说明四边形ABA′B′是矩形.
查看答案和解析>>
科目:czsx
来源:
题型:
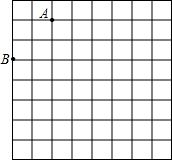
如图是规格为8×8的正方形网格(小正方形的边长为1,小正方形的顶点叫格点),在网格中建立平面直角坐标系,使A点坐标为(-2,4),B点坐标为(-4,2);在第二象限内的格点上找点C(C点的横坐标大于-3),使点C与线段AB组成一个以AB为底的等腰三角形,则C点坐标是
(-2,2)或(-1,1)
(-2,2)或(-1,1)
.
查看答案和解析>>
科目:czsx
来源:
题型:
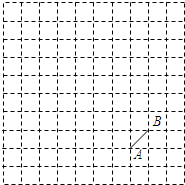
(2012•安庆二模)如图是规格为10×10的正方形网格,请在所给网格中按下列要求操作:
(1)请在网格中建立平面直角坐标系,使点A、B的坐标分别为(1,-2)、(2,-1);
(2)以坐标原点O为位似中心,在第二象限内将线段AB放大到原来的2倍得到线段A
1B
1;
(3)在第二象限内的格点(横、纵坐标均为整数的点叫做格点)上画一点C
1,使点C
1与线段A
1B
1组成一个以A
1B
1为底边的等腰三角形,且腰长是无理数.此时,点C
1的坐标是
(-1,1)
(-1,1)
,△A
1B
1C
1的周长是
(写出一种符合要求的情况即可,结果保留根号).
查看答案和解析>>
科目:czsx
来源:
题型:
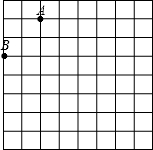
如图是规格为8×8的正方形网格(小正方形的边长为1,小正方形的顶点叫格点),请在所给网格中按下列要求操作:
(1)请在网格中建立平面直角坐标系,使A点坐标为(-2,4),B点坐标为(-4,2);
(2)按(1)中的直角坐标系在第二象限内的格点上找点C(C点的横坐标大于-3),使点C与线段AB组成一个以AB为底的等腰三角形,则C点坐标是
,△ABC的面积是
.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
如图是规格为8×8的正方形网格(网格小正方形的边长为1),请在所给网格中按下列要求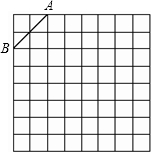 操作:
操作:
(1)请在网格中建立平面直角坐标系,使A点坐标为(-2,3),B点坐标为(-4,1);
(2)在第二象限内的格点上画一点C,使点C与线段AB围成一个直角三角形(不是等腰直角三角形),则C点坐标是______,△ABC的面积是______;
(3)将(2)中画出△ABC以点C为旋转中心,逆时针旋转90°后得△A′B′C.求经过B、C、B′三点的抛物线的解析式;并判断抛物线是否经过8×8正方形网格的格点(不包括点B、C、B′),若经过,请你直接写出点坐标.
查看答案和解析>>
科目:czsx
来源:辽宁省期末题
题型:操作题
如图是规格为8×8的正方形网格,请在所给网格中按下列要求操作:
(1)请在网格中建立平面直角坐标系,使A点坐标为(﹣2,4),B点坐标为(﹣4,2);
(2)在第二象限内的格点上画一点C,使点C与线段AB组成一个以AB为底的等腰三角形,且腰长是无理数,则C点坐标是 ,△ABC的周长是 (结果保留根号); (3)画出△ABC以点C为旋转中心,旋转180°后的△A'B'C,连接AB'和A'B,试说出四边形ABA'B'是何特殊四边形,并说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
 如图是规格为8×8的正方形网格,请在所给网格中按下列要求操作:
如图是规格为8×8的正方形网格,请在所给网格中按下列要求操作:
(1)请在网格中建立平面直角坐标系,使A点坐标为(-2,4),B点坐标为(-4,2);
(2)在第二象限内的格点上画一点C,使点C与线段AB组成一个以AB为底的等腰三角形,且腰长是无理数,则C点坐标是______,△ABC的周长是______(结果保留根号);
(3)画出△ABC以点C为旋转中心,旋转180°后的△A′B′C,连接AB′和A′B,试说出四边形ABA′B′是何特殊四边形,并说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
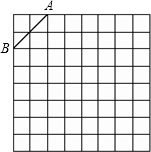 如图是规格为8×8的正方形网格,请在所给网格中按下列要求操作:
如图是规格为8×8的正方形网格,请在所给网格中按下列要求操作:
在网格中建立平面直角坐标系,以O点为坐标原点,使A点坐标为(-3,5),B点坐标为(-5,3).
(1)C点坐标为(-2,0),则△ABC是______三角形;
(2)在第二象限内的格点上找点P,使点P与线段AB组成等腰三角形,且腰长是无理数,写出所有符合条件的P点坐标______.
查看答案和解析>>
科目:czsx
来源:
题型:
如图是规格为8×8的正方形网格,请在所给网格中按下列要求操作:
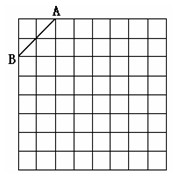
在网格中建立平面直角坐标系, 以O点为坐标原点,使A点坐标为(-3,5),B点坐标为(-5,3).
(1)C点坐标为(-2,0),则 是 三角形;
是 三角形;
(2)在第二象限内的格点上找点P, 使点P与线段AB组成等腰三角形, 且腰长是无理数, 写出所有符合条件的P点坐标 .
查看答案和解析>>
科目:czsx
来源:
题型:解答题
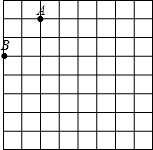 如图是规格为8×8的正方形网格(小正方形的边长为1,小正方形的顶点叫格点),请在所给网格中按下列要求操作:
如图是规格为8×8的正方形网格(小正方形的边长为1,小正方形的顶点叫格点),请在所给网格中按下列要求操作:
(1)请在网格中建立平面直角坐标系,使A点坐标为(-2,4),B点坐标为(-4,2);
(2)按(1)中的直角坐标系在第二象限内的格点上找点C(C点的横坐标大于-3),使点C与线段AB组成一个以AB为底的等腰三角形,则C点坐标是______,△ABC的面积是______.
查看答案和解析>>
科目:czsx
来源:北京市四中2011-2012学年七年级下学期期中考试数学试题
题型:022
如图是规格为8×8的正方形网格(小正方形的边长为1,小正方形的顶点叫格点),在网格中建立平面直角坐标系,使A点坐标为(-2,4),B点坐标为(-4,2);在第二象限内的格点上找点C(C点的横坐标大于-3),使点C与线段AB组成一个以AB为底的等腰三角形,则C点坐标是________.

查看答案和解析>>
科目:czsx
来源:
题型:解答题
如图是规格为8×8的正方形网格,请在网格中按下列要求操作:
(1)在第二象限内的格点上画一点C,使点C与线段AB组成一个以AB为底的等腰三角形,且腰长是无理数,并求出腰长;
(2)画出△ABC绕点C旋转180°后得到的△A′B′C;连接AB′和A′B,试说明四边形ABA′B′是矩形.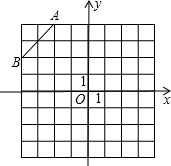
查看答案和解析>>
科目:czsx
来源:
题型:解答题
 如图是规格为10×10的正方形网格,请在所给网格中按下列要求操作:
如图是规格为10×10的正方形网格,请在所给网格中按下列要求操作:
(1)请在网格中建立平面直角坐标系,使点A、B的坐标分别为(1,-2)、(2,-1);
(2)以坐标原点O为位似中心,在第二象限内将线段AB放大到原来的2倍得到线段A1B1;
(3)在第二象限内的格点(横、纵坐标均为整数的点叫做格点)上画一点C1,使点C1与线段A1B1组成一个以A1B1为底边的等腰三角形,且腰长是无理数.此时,点C1的坐标是______,△A1B1C1的周长是______(写出一种符合要求的情况即可,结果保留根号).
查看答案和解析>>
科目:czsx
来源:
题型:
如图是规格为8×8的正方形网格,请在所给网格中按下列要求操作:
在网格中建立平面直角坐标系, 以O点为坐标原点,使A点坐标为(-3,5),B点坐标为(-5,3).
(1)C点坐标为(-2,0),则 是 三角形;
是 三角形;
(2)在第二象限内的格点上找点P, 使点P与线段AB组成等腰三角形, 且腰长是无理数, 写出所有符合条件的P点坐标 .

查看答案和解析>>
科目:czsx
来源:北京同步题
题型:解答题
如图是规格为8 ×8 的正方形网格( 小正方形的边长为1 ,小正方形的顶点叫格点) ,请在所给网格中按下列要求操作:
(1)请在网格中建立平面直角坐标系,使A点坐标为(-2,4),B点坐标为(-4,2);
(2)按(1)中的直角坐标系在第二象限内的格点上找点C(C点的横坐标大于-3),使点C与线段AB组成一个以AB为底的等腰三角形,则C点坐标是______,△ABC的面积是______.
查看答案和解析>>
科目:czsx
来源:
题型:填空题
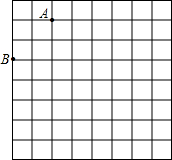 如图是规格为8×8的正方形网格(小正方形的边长为1,小正方形的顶点叫格点),在网格中建立平面直角坐标系,使A点坐标为(-2,4),B点坐标为(-4,2);在第二象限内的格点上找点C(C点的横坐标大于-3),使点C与线段AB组成一个以AB为底的等腰三角形,则C点坐标是________.
如图是规格为8×8的正方形网格(小正方形的边长为1,小正方形的顶点叫格点),在网格中建立平面直角坐标系,使A点坐标为(-2,4),B点坐标为(-4,2);在第二象限内的格点上找点C(C点的横坐标大于-3),使点C与线段AB组成一个以AB为底的等腰三角形,则C点坐标是________.
查看答案和解析>>
科目:czsx
来源:
题型:
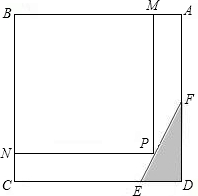
如图,规格为60cm×60cm的正方形地砖在运输过程中受损,断去一角,量得AF=30cm,CE=45cm,现准备从五边形地砖ABCEF上截出一个面积为S的矩形地砖PMBN,
(1)设BN=x,BM=y,请用含x的代数式表示y,并写出x的取值范围;
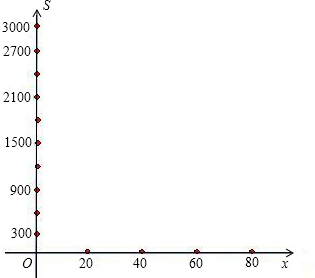
(2)请用含x的代数式表示S,并在给定的直角坐标系内画出该函数的示意图;
(3)利用函数图象回答(2)中:当x取何值时,S有最大值?最大值是多少?
查看答案和解析>>

 如图是规格为8×8的正方形网格,请在所给网格中按下列要求操作:
如图是规格为8×8的正方形网格,请在所给网格中按下列要求操作: 如图是规格为8×8的正方形网格,请在所给网格中按下列要求操作:
如图是规格为8×8的正方形网格,请在所给网格中按下列要求操作: 操作:
操作:
 如图是规格为8×8的正方形网格(小正方形的边长为1,小正方形的顶点叫格点),在网格中建立平面直角坐标系,使A点坐标为(-2,4),B点坐标为(-4,2);在第二象限内的格点上找点C(C点的横坐标大于-3),使点C与线段AB组成一个以AB为底的等腰三角形,则C点坐标是
如图是规格为8×8的正方形网格(小正方形的边长为1,小正方形的顶点叫格点),在网格中建立平面直角坐标系,使A点坐标为(-2,4),B点坐标为(-4,2);在第二象限内的格点上找点C(C点的横坐标大于-3),使点C与线段AB组成一个以AB为底的等腰三角形,则C点坐标是 (2012•安庆二模)如图是规格为10×10的正方形网格,请在所给网格中按下列要求操作:
(2012•安庆二模)如图是规格为10×10的正方形网格,请在所给网格中按下列要求操作: 如图是规格为8×8的正方形网格(小正方形的边长为1,小正方形的顶点叫格点),请在所给网格中按下列要求操作:
如图是规格为8×8的正方形网格(小正方形的边长为1,小正方形的顶点叫格点),请在所给网格中按下列要求操作: 操作:
操作: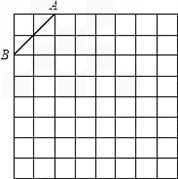
 如图是规格为8×8的正方形网格,请在所给网格中按下列要求操作:
如图是规格为8×8的正方形网格,请在所给网格中按下列要求操作: 如图是规格为8×8的正方形网格,请在所给网格中按下列要求操作:
如图是规格为8×8的正方形网格,请在所给网格中按下列要求操作:![]() 是 三角形;
是 三角形;
 如图是规格为8×8的正方形网格(小正方形的边长为1,小正方形的顶点叫格点),请在所给网格中按下列要求操作:
如图是规格为8×8的正方形网格(小正方形的边长为1,小正方形的顶点叫格点),请在所给网格中按下列要求操作:

 如图是规格为10×10的正方形网格,请在所给网格中按下列要求操作:
如图是规格为10×10的正方形网格,请在所给网格中按下列要求操作:![]() 是 三角形;
是 三角形;

 如图是规格为8×8的正方形网格(小正方形的边长为1,小正方形的顶点叫格点),在网格中建立平面直角坐标系,使A点坐标为(-2,4),B点坐标为(-4,2);在第二象限内的格点上找点C(C点的横坐标大于-3),使点C与线段AB组成一个以AB为底的等腰三角形,则C点坐标是________.
如图是规格为8×8的正方形网格(小正方形的边长为1,小正方形的顶点叫格点),在网格中建立平面直角坐标系,使A点坐标为(-2,4),B点坐标为(-4,2);在第二象限内的格点上找点C(C点的横坐标大于-3),使点C与线段AB组成一个以AB为底的等腰三角形,则C点坐标是________. 如图,规格为60cm×60cm的正方形地砖在运输过程中受损,断去一角,量得AF=30cm,CE=45cm,现准备从五边形地砖ABCEF上截出一个面积为S的矩形地砖PMBN,
如图,规格为60cm×60cm的正方形地砖在运输过程中受损,断去一角,量得AF=30cm,CE=45cm,现准备从五边形地砖ABCEF上截出一个面积为S的矩形地砖PMBN,