直角三角形的三边为a-b，a，a+b且ab都为整数答案解析
科目：czsx
来源：
题型：
勾股定理有着悠久的历史，它曾引起很多人的兴趣．l955年希腊发行了二枚以勾股图为背景的邮票．所谓勾股图是指以直角三角形的三边为边向外作正方形构成，它可以验证勾股定理．在上图的勾股图中，已知∠ACB=90°，∠BAC=30°，AB=8．作△PQR使得∠R=90°，点H在边QR上，点D，E在边PR上，点G，F在边PQ上，那么△PQR的周长等于
．
查看答案和解析>>
科目：czsx
来源：
题型：
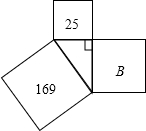
以直角三角形的三边为边长分别向外作正方形，如图字母B所代表的正方形的面积是（ ）
查看答案和解析>>
科目：czsx
来源：
题型：
如图，△ABC中，∠C=90°．
（1）以直角三角形的三边为边向形外作等边三角形（如图①），探究S
1+S
2与S
3的关系；
（2）以直角三角形的三边为斜边向形外作等腰直角三角形（如图②），探究S
1+S
2与S
3的关系；
（3）以直角三角形的三边为直径向形外作半圆（如图③），探究S
1+S
2与S
3的关系．
查看答案和解析>>
科目：czsx
来源：
题型：
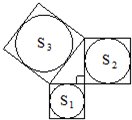
5、如下图，分别以直角三角形的三边为边长向外作正方形，然后分别以三个正方形的中心为圆心，正方形边长的一半为半径作圆，记三个圆的面积分别为S
1，S
2，S
3，则S
1，S
2，S
3之间的关系是（ ）
查看答案和解析>>
科目：czsx
来源：
题型：
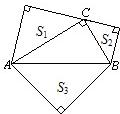
22、如图，分别以直角三角形的三边为斜边，在其形外作等腰直角三角形，其面积分别记为S
1、S
2、S
3，则S
1、S
2、S
3的关系为（ ）
查看答案和解析>>
科目：czsx
来源：
题型：
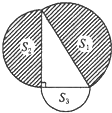
如图，分别以直角三角形的三边为直径作半圆，则三个半圆的面积S
1，S
2+S
3之间的关系是（ ）
| A、S1＞S2+S3 | B、S1=S2+S3 | C、S1＜S2+S3 | D、无法确定 |
查看答案和解析>>
科目：czsx
来源：
题型：
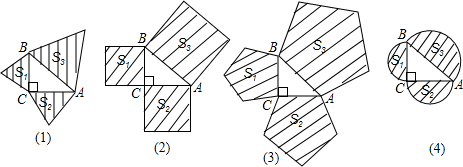
下列图①、②、③中的阴影部分分别是以直角三角形的三边为边长所作的正多边形；图④中的阴影部分分别是以直角三角形的三边为直径所作的半圆．根据勾股定理可知：分别以直角三角形的两条直角边为边长的正方形面积之和等于以斜边为边长的正方形的面积（如图②）
（1）类似的结论，对于图②的结论，对于图①、③、④是否成立？如果成立，请选择其中一个图形进行证明．
（2）根据（1）的结论，你能提出一般性的结论吗？写出你的结论并给予证明．
查看答案和解析>>
科目：czsx
来源：
题型：
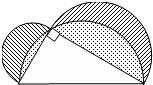
已知直角三角形的一直角边长是4，以这个直角三角形的三边为直径作三个半圆（如图所示），已知两个月牙形（带斜线的阴影图形）的面积之和是10，那么以下四个整数中，最接近图中两个弓形（带点的阴影图形）面积之和的是（ ）
查看答案和解析>>
科目：czsx
来源：
题型：
如果直角三角形的三边为3，6，m，那么m的取值可以有（ ）
查看答案和解析>>
科目：czsx
来源：
题型：
（1）已知实数x、y满足（x
2+y
2）（x
2-1+y
2）=12，则x
2+y
2的值为
4
4
．
（2）已知方程x
2-5x+2=0的一根为a，那么a+
的值为
5
5
．
（3）已知关于x的方程x
2-
x+k=0有两个不相等的实数解，化简|-k-2|+
=
4
4
．
（4）已知一直角三角形的三边为a、b、c，∠B=90°，那么关于x的方程a（x
2-1）-2cx+b（x
2+1）=0的根的情况为
方程有两个相等的实数根
方程有两个相等的实数根
．
（5）如果关于x的方程（m-2）x
2-2（m-1）x+m=0只有一个实数根，那么方程mx
2-（m+2）x+（4-m）=0的根的情况是
方程有两个相等的实数根
方程有两个相等的实数根
．
查看答案和解析>>
科目：czsx
来源：
题型：
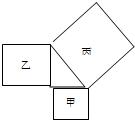
7、如图，以直角三角形的三边为边向三角形外作正方形，已知甲、乙两个正方形的面积分别为4、6，则丙正方形的面积为
10
．
查看答案和解析>>
科目：czsx
来源：
题型：
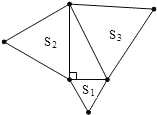
如图，分别以直角三角形的三边为边长向外作等边三角形，面积分别记为S
1，S
2，S
3，则S
1，S
2，S
3的关系是（ ）
| A、S1+S2=S3 | B、S12+S22=S32 | C、S1+S2＞S3 | D、S1+S2＜S3 |
查看答案和解析>>
科目：czsx
来源：
题型：
10、一个直角三角形的三边为三个连续偶数，则它的三边长分别为
6，8，10
．
查看答案和解析>>
科目：czsx
来源：
题型：
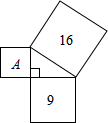
如图，以直角三角形的三边为边长分别作三个正方形，其中两个正方形的面积标示在图中，则字母A所在的正方形的面积是
7
7
．
查看答案和解析>>
科目：czsx
来源：
题型：
如图所示，分别以直角三角形的三边为直径作半圆，其中两个半圆的面积S
1=
π，S
3=
π，则S
2=
2π
2π
．
查看答案和解析>>
科目：czsx
来源：
题型：
（拓展创新）在教材中，我们通过数格子的方法发现了直角三角形的三边关系，利用完全相同的四个直角三角形采用拼图的方式验证了勾股定理的正确性．
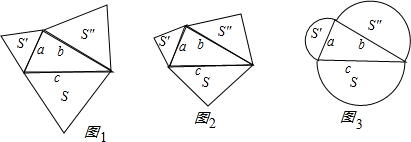
问题1：以直角三角形的三边为边向形外作等边三角形，探究S
1+S
2与S
3的关系（如图1）．
问题2：以直角三角形的三边为斜边向形外作等腰直角三角形，探究S′+S″与S的关系（如图2）．
问题3：以直角三角形的三边为直径向形外作半圆，探究S
1+S
2与S
3的关系（如图3）．
查看答案和解析>>
科目：czsx
来源：
题型：
以直角三角形的三边为边分别向外作等边三角形，两直角边上的等边三角形的面积分别记作s1、s2，斜边上的等边三角形的面积记作s3，则s1、s2、s3之间的关系是（ ）
| | | |
查看答案和解析>>
科目：czsx
来源：
题型：
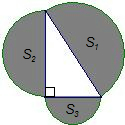
（2012•新疆）如图所示，分别以直角三角形的三边为直径作半圆，其中两个半圆的面积
S1=π，S
2=2π，则S
3是
．
查看答案和解析>>
科目：czsx
来源：
题型：
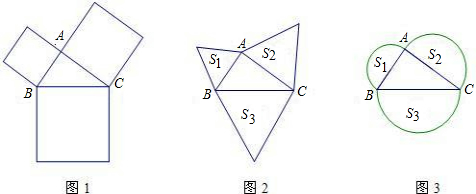
勾股定理有着悠久的历史，它曾引起很多人的兴趣．1955年希腊发行了二枚以勾股图为背景的邮票．所谓勾股图是指以直角三角形的三边为边向外作正方形构成（图1：△ABC中，∠BAC=90°）．
请解答：
（1）如图2，若以直角三角形的三边为边向外作等边三角形，则它们的面积S
1、S
2、S
3之间的数量关系是
．
（2）如图3，若以直角三角形的三边为直径向外作半圆，则它们的面积S
1、S
2、S
3之间的数量关系是
，请说明理由．
（3）如图4，在梯形ABCD中，AD∥BC，∠ABC+∠BCD=90°，BC=2AD，分别以AB、CD、AD为边向
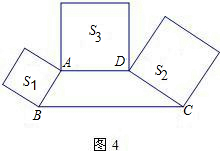
梯形外作正方形，其面积分别为S
1、S
2、S
3，则S
1、S
2、S
3之间的数量关系式为
，请说明理由．
查看答案和解析>>
科目：czsx
来源：
题型：
观察下列图形，回答问题：
问题（1）：若图①中的△DEF为直角三角形，正方形P的面积为9，正方形Q的面积为15，则正方形M的面积为
24
24
．
问题（2）：如图②，分别以直角三角形的三边为直径向三角形外作三个半圆，这三个半圆的面积之间的关系是
S1+S2=S3
S1+S2=S3
（用图中字母表示）
问题（3）：如图③，如果直角三角形两直角边的长分别为3和4，以直角三角形的三边为直径作半圆，请你利用上面中的结论求出阴影部分的面积．
查看答案和解析>>
