
科目:czsx 来源:江苏省张家港市2012届九年级上学期期中考试数学试题 题型:022
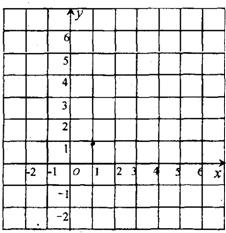
已知二次函数y=-x2+2x+m的部分图象如图所示,则函数与x轴两交点坐标是________

科目:czsx 来源: 题型:
 21、已知二次函数y=-(x-2)2+4.
21、已知二次函数y=-(x-2)2+4.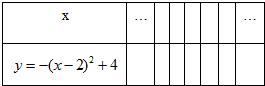
科目:czsx 来源: 题型:
| S四边形CFGH |
| S四边形CMNO |
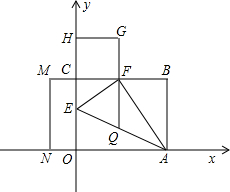 CO=1,CE=
CO=1,CE=| 1 |
| 3 |
| 2 |
| 3 |
2
| ||
| 3 |
| 1 |
| 3 |
2
| ||
| 3 |
| 1 |
| 3 |
科目:czsx 来源: 题型:
科目:czsx 来源: 题型:
科目:czsx 来源: 题型:
A、(-
| ||||
| B、(-1,2) | ||||
| C、(-1,-2) | ||||
| D、(-1,0) |
科目:czsx 来源: 题型:
| 3 |
| 4 |
| 3 |
| 3 |
| 4 |
| 3 |
| 3 |
| 13 |
