如图，抛物线y=ax2+bx+c与x轴的答案解析

科目：czsx 来源： 题型：

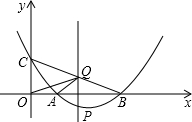
已知：如图，抛物线y=ax²+bx+2与x轴的交点是A（3，0）、B（6，0），与y轴的交点是C．
（1）求抛物线的函数表达式；
（2）设P（x，y）（0＜x＜6）是抛物线上的动点，过点P作PQ∥y轴交直线BC于点Q．
①当x取何值时，线段PQ的长度取得最大值，其最大值是多少？
②是否存在这样的点P，使△OAQ为直角三角形？若存在，求出点P的坐标；若不存在，请说明理由．

科目：czsx 来源： 题型：

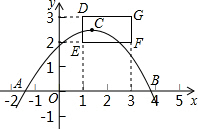
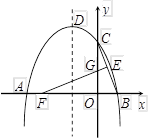
如图，抛物线y=ax²+bx+c与x轴的一个交点A在点（-2，0）和（-1，0）之间（包括这两点），顶点C是矩形DEFG上（包括边界和内部）的一个动点，则abc

＜

＜

0（填“＞”或“＜”）

科目：czsx 来源： 题型：

如图，抛物线y=ax²+bx+4与x轴的两个交点分别为A（-4，0）、B（2，0），与y轴交于点C，顶点为D．E（1，2）为线段BC的中点，BC的垂直平分线与x轴、y轴分别交于F、G．
（1）求抛物线的函数解析式，并写出顶点D的坐标；
（2）在直线EF上求一点H，使△CDH的周长最小，并求出最小周长；
（3）若点K在x轴上方的抛物线上运动，当K运动到什么位置时，△EFK的面积最大？并求出最大面积．

科目：czsx 来源： 题型：

如图，抛物线y=ax²+bx+c与x轴的一个交点A在点（-2，0）和（-1，0）之间（包括这两点），顶点C是矩形DEFG上（包括边界和内部）的一个动点，则：
（1）abc

 

0（填“＞”或“＜”）；
（2）a的取值范围是

 

．

科目：czsx 来源：第2章《二次函数》中考题集（31）：2.8 二次函数的应用（解析版） 题型：解答题

如图，抛物线y=ax²+bx+4与x轴的两个交点分别为A（-4，0）、B（2，0），与y轴交于点C，顶点为D．E（1，2）为线段BC的中点，BC的垂直平分线与x轴、y轴分别交于F、G．
（1）求抛物线的函数解析式，并写出顶点D的坐标；
（2）在直线EF上求一点H，使△CDH的周长最小，并求出最小周长；
（3）若点K在x轴上方的抛物线上运动，当K运动到什么位置时，△EFK的面积最大？并求出最大面积．

科目：czsx 来源：2013年浙江省湖州市中考数学模拟试卷（十二）（解析版） 题型：填空题

如图，抛物线y=ax²+bx+c与x轴的一个交点A在点（-2，0）和（-1，0）之间（包括这两点），顶点C是矩形DEFG上（包括边界和内部）的一个动点，则：
（1）abc    0（填“＞”或“＜”）；
（2）a的取值范围是    ．

科目：czsx 来源：2012年浙江省杭州市中考数学模拟试卷（30）（解析版） 题型：填空题

如图，抛物线y=ax²+bx+c与x轴的一个交点A在点（-2，0）和（-1，0）之间（包括这两点），顶点C是矩形DEFG上（包括边界和内部）的一个动点，则abc    0（填“＞”或“＜”）

科目：czsx 来源：2010年高级中等学校招生全国统一考试数学卷（辽宁沈阳） 题型：解答题

科目：czsx 来源：第23章《二次函数与反比例函数》中考题集（28）：23.5 二次函数的应用（解析版） 题型：解答题

如图，抛物线y=ax²+bx+4与x轴的两个交点分别为A（-4，0）、B（2，0），与y轴交于点C，顶点为D．E（1，2）为线段BC的中点，BC的垂直平分线与x轴、y轴分别交于F、G．
（1）求抛物线的函数解析式，并写出顶点D的坐标；
（2）在直线EF上求一点H，使△CDH的周长最小，并求出最小周长；
（3）若点K在x轴上方的抛物线上运动，当K运动到什么位置时，△EFK的面积最大？并求出最大面积．

科目：czsx 来源：2011-2012学年浙江省金华市九年级（上）期末数学试卷（解析版） 题型：填空题

如图，抛物线y=ax²+bx+c与x轴的一个交点A在点（-2，0）和（-1，0）之间（包括这两点），顶点C是矩形DEFG上（包括边界和内部）的一个动点，则：
（1）abc    0（填“＞”或“＜”）；
（2）a的取值范围是    ．

科目：czsx 来源：2010-2011学年陕西省师大附中九年级（上）期末数学试卷（解析版） 题型：解答题

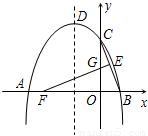
如图，抛物线y=ax²+bx+4与x轴的两个交点分别为A（-4，0）、B（2，0），与y轴交于点C，顶点为D．E（1，2）为线段BC的中点，BC的垂直平分线与x轴、y轴分别交于F、G．
（1）求抛物线的函数解析式，并写出顶点D的坐标；
（2）在直线EF上求一点H，使△CDH的周长最小，并求出最小周长；
（3）若点K在x轴上方的抛物线上运动，当K运动到什么位置时，△EFK的面积最大？并求出最大面积．

科目：czsx 来源： 题型：

科目：czsx 来源： 题型：

如图，抛物线y = ax² + bx + 4与x轴的两个交点分别为A（－4，0）、B（2，0），与y轴交于点C，顶点为D．E（1，2）为线段BC的中点，BC的垂直平分线与x轴、y轴分别交于F、G．

（1）求抛物线的函数解析式，并写出顶点D的坐标；
（2）在直线EF上求一点H，使△CDH的周长最小，并求出最小周长；
（3）若点K在x轴上方的抛物线上运动，当K运动到什么位置时，
△EFK的面积最大？并求出最大面积．

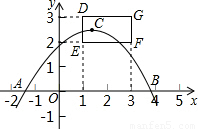
科目：czsx 来源：2011-2012学年浙江省杭州市萧山区朝晖中学九年级（上）第一次月考数学试卷（解析版） 题型：填空题

如图，抛物线y=ax²+bx+c与x轴的一个交点A在点（-2，0）和（-1，0）之间（包括这两点），顶点C是矩形DEFG上（包括边界和内部）的一个动点，则：
（1）abc    0（填“＞”或“＜”）；
（2）a的取值范围是    ．

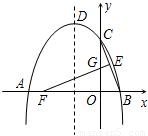
科目：czsx 来源：2010年全国中考数学试题汇编《二次函数》（08）（解析版） 题型：解答题

（2010•绵阳）如图，抛物线y=ax²+bx+4与x轴的两个交点分别为A（-4，0）、B（2，0），与y轴交于点C，顶点为D．E（1，2）为线段BC的中点，BC的垂直平分线与x轴、y轴分别交于F、G．
（1）求抛物线的函数解析式，并写出顶点D的坐标；
（2）在直线EF上求一点H，使△CDH的周长最小，并求出最小周长；
（3）若点K在x轴上方的抛物线上运动，当K运动到什么位置时，△EFK的面积最大？并求出最大面积．

科目：czsx 来源：第26章《二次函数》中考题集（28）：26.3 实际问题与二次函数（解析版） 题型：解答题

如图，抛物线y=ax²+bx+4与x轴的两个交点分别为A（-4，0）、B（2，0），与y轴交于点C，顶点为D．E（1，2）为线段BC的中点，BC的垂直平分线与x轴、y轴分别交于F、G．
（1）求抛物线的函数解析式，并写出顶点D的坐标；
（2）在直线EF上求一点H，使△CDH的周长最小，并求出最小周长；
（3）若点K在x轴上方的抛物线上运动，当K运动到什么位置时，△EFK的面积最大？并求出最大面积．

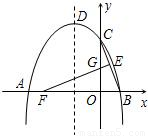
科目：czsx 来源：第2章《二次函数》中考题集（28）：2.4 二次函数的应用（解析版） 题型：解答题

如图，抛物线y=ax²+bx+4与x轴的两个交点分别为A（-4，0）、B（2，0），与y轴交于点C，顶点为D．E（1，2）为线段BC的中点，BC的垂直平分线与x轴、y轴分别交于F、G．
（1）求抛物线的函数解析式，并写出顶点D的坐标；
（2）在直线EF上求一点H，使△CDH的周长最小，并求出最小周长；
（3）若点K在x轴上方的抛物线上运动，当K运动到什么位置时，△EFK的面积最大？并求出最大面积．

科目：czsx 来源：2009-2010学年浙江省杭州市萧山区朝晖中学九年级（上）数学阶段性测试（解析版） 题型：填空题

如图，抛物线y=ax²+bx+c与x轴的一个交点A在点（-2，0）和（-1，0）之间（包括这两点），顶点C是矩形DEFG上（包括边界和内部）的一个动点，则：
（1）abc    0（填“＞”或“＜”）；
（2）a的取值范围是    ．

科目：czsx 来源：2012年广东省广州市中考数学模拟试卷（四）（解析版） 题型：解答题

如图，抛物线y=ax²+bx+4与x轴的两个交点分别为A（-4，0）、B（2，0），与y轴交于点C，顶点为D．E（1，2）为线段BC的中点，BC的垂直平分线与x轴、y轴分别交于F、G．
（1）求抛物线的函数解析式，并写出顶点D的坐标；
（2）在直线EF上求一点H，使△CDH的周长最小，并求出最小周长；
（3）若点K在x轴上方的抛物线上运动，当K运动到什么位置时，△EFK的面积最大？并求出最大面积．

科目：czsx 来源：2012年四川省成都市石室天府中学中考数学三模试卷（解析版） 题型：解答题

如图，抛物线y=ax²+bx+4与x轴的两个交点分别为A（-4，0）、B（2，0），与y轴交于点C，顶点为D．E（1，2）为线段BC的中点，BC的垂直平分线与x轴、y轴分别交于F、G．
（1）求抛物线的函数解析式，并写出顶点D的坐标；
（2）在直线EF上求一点H，使△CDH的周长最小，并求出最小周长；
（3）若点K在x轴上方的抛物线上运动，当K运动到什么位置时，△EFK的面积最大？并求出最大面积．