
科目:czsx 来源: 题型:
科目:czsx 来源: 题型:
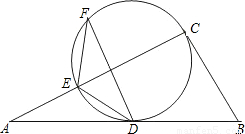
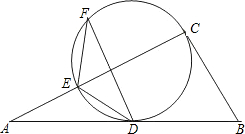 D、C,并交AC边于E.在优弧DE上任取一点F,连接FE、FD,若BC=a,cos∠EFD=
D、C,并交AC边于E.在优弧DE上任取一点F,连接FE、FD,若BC=a,cos∠EFD=| AC | AB |
科目:czsx 来源:2010年福建省南安市初中学业质量检查数学试题 题型:044
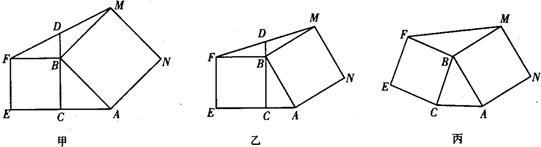
如图,在△ABC中,AB=BC,P为AB边上一点,连接CP,以PA、PC为邻边作□APCD,AC与PD相交于点E,已知∠ABC=∠AEP=α(0°<α<90°).
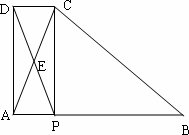
(1)求证:∠EAP=∠EPA;
(2)□APCD是否为矩形?请说明理由;
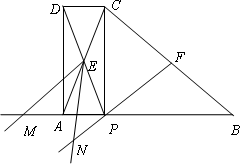
(3)如图,F为BC中点,连接FP,将∠AEP绕点E顺时针旋转适当的角度,得到∠MEN(点M、N分别是∠MEN的两边与BA、FP延长线的交点).猜想线段EM与EN之间的数量关系,并证明你的结论.

科目:czsx 来源:2003年全国中考数学试题汇编《三角形》(09)(解析版) 题型:解答题
 .
.
科目:czsx 来源: 题型:解答题
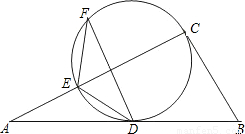
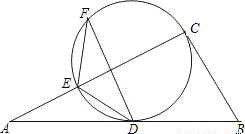
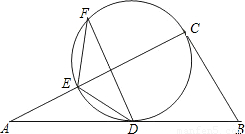
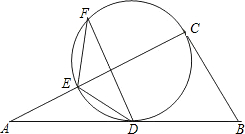 D、C,并交AC边于E.在优弧DE上任取一点F,连接FE、FD,若BC=a,cos∠EFD=
D、C,并交AC边于E.在优弧DE上任取一点F,连接FE、FD,若BC=a,cos∠EFD=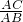 .
.科目:czsx 来源: 题型:解答题



科目:czsx 来源:2003年全国中考数学试题汇编《圆》(11)(解析版) 题型:解答题
 .
.
科目:czsx 来源:同步题 题型:操作题

科目:czsx 来源:2003年全国中考数学试题汇编《锐角三角函数》(04)(解析版) 题型:解答题
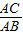 .
.
科目:czsx 来源:2008年四川省绵阳市中考数学试卷(副卷)(解析版) 题型:解答题


科目:czsx 来源:2003年湖北省黄石市中考数学试卷(解析版) 题型:解答题
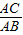 .
.
科目:czsx 来源:福建省南平市2010年中考数学试题 题型:044
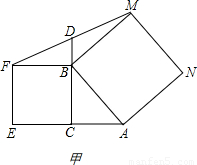
如图,在△ABC中,AB=BC,P为AB边上一点,连接CP,以PA、PC为邻边作□APCD,AC与PD相交于点E,已知∠ABC=∠AEP=α(0°<α<90°).
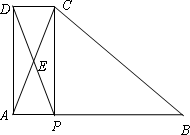
(1)求证:∠EAP=∠EPA;
(2)□APCD是否为矩形?请说明理由;
(3)如图,F为BC中点,连接FP,将∠AEP绕点E顺时针旋转适当的角度,得到∠MEN(点M、N分别是∠MEN的两边与BA、FP延长线的交点).猜想线段EM与EN之间的数量关系,并证明你的结论.
科目:czsx 来源: 题型:
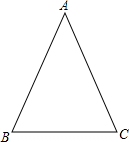 如图,在△ABC中,AB=AC,∠A=36°,
如图,在△ABC中,AB=AC,∠A=36°,| CD | DA |
科目:czsx 来源: 题型:
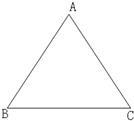 23、如图,在△ABC中,用尺规作∠ABC的平分线BD,交AC于D,作线段BD的垂直平分线EF,分别交AB于E,BC于F,垂足为O,连接DE、DF,判断四边形BFDE的形状,并加以证明.(不写作法,保留作图痕迹)
23、如图,在△ABC中,用尺规作∠ABC的平分线BD,交AC于D,作线段BD的垂直平分线EF,分别交AB于E,BC于F,垂足为O,连接DE、DF,判断四边形BFDE的形状,并加以证明.(不写作法,保留作图痕迹)科目:czsx 来源: 题型:
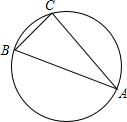 △ABC中,∠A=30°,∠C=90°,作△ABC的外接圆.如图,若
△ABC中,∠A=30°,∠C=90°,作△ABC的外接圆.如图,若 |
| AB |
 |
| AC |
| A、10cm | B、9cm |
| C、8cm | D、6cm |
科目:czsx 来源: 题型:
 如图,在△ABC中,AD⊥BC,垂足为D.
如图,在△ABC中,AD⊥BC,垂足为D.科目:czsx 来源: 题型:
 (2011•杭州一模)如图,在△ABC中,AB=AC=
(2011•杭州一模)如图,在△ABC中,AB=AC=| 5 |
科目:czsx 来源: 题型:
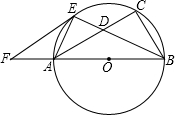 ∥AC交BA的延长线于F.
∥AC交BA的延长线于F.