科目:czsx
来源:
题型:
圆外切等腰梯形一腰长为5cm,则梯形的中位线长为( )
查看答案和解析>>
科目:czsx
来源:2012年湖南省常德市中考数学模拟试卷(六)(解析版)
题型:选择题
圆外切等腰梯形一腰长为5cm,则梯形的中位线长为( )
A.10cm
B.5cm
C.20cm
D.15cm
查看答案和解析>>
科目:czsx
来源:
题型:单选题
圆外切等腰梯形一腰长为5cm,则梯形的中位线长为
- A.
10cm
- B.
5cm
- C.
20cm
- D.
15cm
查看答案和解析>>
科目:czsx
来源:
题型:
圆外切等腰梯形一腰长为5cm,则梯形的中位线长为( )
A 10cm B 5cm C 20cm D 15cm
查看答案和解析>>
科目:czsx
来源:
题型:
(2012•黑龙江)等腰三角形一腰长为5,一边上的高为4,则底边长
.
查看答案和解析>>
科目:czsx
来源:
题型:
(1997•北京)如果等腰三角形一腰长为8,底边长为10,那么连接这个三角形各边的中点所成的三角形的周长为( )
查看答案和解析>>
科目:czsx
来源:
题型:
一个圆锥的三视图如图所示,主视图,左视图是两个全等的等腰三角形,腰长为12cm,底边长为10cm,则该圆锥的侧面展开图的圆心角为
150°
150°
.

查看答案和解析>>
科目:czsx
来源:
题型:
已知:一个等腰直角三角形腰长为a,三边上的高之积为P,一个等边三角形边长为a,三边上的高之积为Q,则P和Q的大小关系是( )
查看答案和解析>>
科目:czsx
来源:
题型:
(2012•佳木斯)等腰三角形一腰长为5,一边上的高为3,则底边长为
.
查看答案和解析>>
科目:czsx
来源:
题型:

6、某几何体的三视图如图所示,主视图、左视图是两个全等的等腰三角形,腰长为13cm,底边长为10cm,则该几何体的侧面积是( )
查看答案和解析>>
科目:czsx
来源:
题型:
7、有一个内角为60°的等腰三角形,腰长为6cm,那么这个三角形的周长为
18
cm.
查看答案和解析>>
科目:czsx
来源:
题型:
19、用8cm长的细铁丝围成一个等腰三角形,腰长为xcm,底长为ycm.
(1)求y关于x的函数关系式;
(2)求自变量x的取值范围;
(3)用描点法画出该函数的图象.
查看答案和解析>>
科目:czsx
来源:
题型:
如图,等腰直角△ABC腰长为a,现分别按图1,图2方式在△ABC内内接一个正方形ADFE和正方形PMNQ.设△ABC的面积为S,正方形ADFE的面积为S
1,正方形PMNQ的面积为S
2.
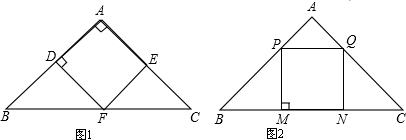
(1)在图1中,求AD:AB的值;在图2中,求AP:AB的值;
(2)比较S
1+S
2与S的大小.
查看答案和解析>>
科目:czsx
来源:2012年初中毕业升学考试(黑龙江龙东地区卷)数学(解析版)
题型:填空题
等腰三角形一腰长为5,一边上的高为3,则底边长为 。
查看答案和解析>>
科目:czsx
来源:2012-2013学年江西景德镇八年级上第一章测试数学试卷(解析版)
题型:填空题
等腰三角形一腰长为5,一边上的高为4,则底边长 .
查看答案和解析>>
科目:czsx
来源:2012年初中毕业升学考试(黑龙江龙东地区卷)数学(带解析)
题型:填空题
等腰三角形一腰长为5,一边上的高为3,则底边长为 。
查看答案和解析>>
科目:czsx
来源:1+1轻巧夺冠·优化训练·八年级数学下
题型:013
如果等腰三角形一腰长为8,底边长为10,那么连接这个三角形各边中点所组成的三角形的周长为
[ ]
查看答案和解析>>
科目:czsx
来源:第1章《解直角三角形》好题集(12):1.4 解直角三角形(解析版)
题型:选择题
已知:一个等腰直角三角形腰长为a,三边上的高之积为P,一个等边三角形边长为a,三边上的高之积为Q,则P和Q的大小关系是( )
A.P>Q
B.P<Q
C.P=Q
D.无法确定
查看答案和解析>>
科目:czsx
来源:2010年上海市宝山区泗塘中学初三数学基础卷(解析版)
题型:解答题
(2009•湘西州)如图,等腰直角△ABC腰长为a,现分别按图1,图2方式在△ABC内内接一个正方形ADFE和正方形PMNQ.设△ABC的面积为S,正方形ADFE的面积为S
1,正方形PMNQ的面积为S
2.
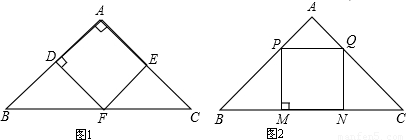
(1)在图1中,求AD:AB的值;在图2中,求AP:AB的值;
(2)比较S
1+S
2与S的大小.
查看答案和解析>>
科目:czsx
来源:2009年湖南省湘西州中考数学试卷(解析版)
题型:解答题
(2009•湘西州)如图,等腰直角△ABC腰长为a,现分别按图1,图2方式在△ABC内内接一个正方形ADFE和正方形PMNQ.设△ABC的面积为S,正方形ADFE的面积为S
1,正方形PMNQ的面积为S
2.

(1)在图1中,求AD:AB的值;在图2中,求AP:AB的值;
(2)比较S
1+S
2与S的大小.
查看答案和解析>>



