
科目:czsx 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
科目:czsx 来源:2009年安徽省合肥市寿春中学一模试卷(解析版) 题型:解答题
 ;勾是五时,股和弦的算式分别是
;勾是五时,股和弦的算式分别是 .根据你发现的规律,分别写出勾是七时,股和弦的算式;
.根据你发现的规律,分别写出勾是七时,股和弦的算式;科目:czsx 来源: 题型:解答题
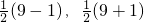 ;勾是五时,股和弦的算式分别是
;勾是五时,股和弦的算式分别是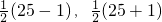 .根据你发现的规律,分别写出勾是七时,股和弦的算式;
.根据你发现的规律,分别写出勾是七时,股和弦的算式;科目:czsx 来源:2012年安徽省合肥市包河区中考数学一模试卷(解析版) 题型:解答题
 ;勾是五时,股和弦的算式分别是
;勾是五时,股和弦的算式分别是 .根据你发现的规律,分别写出勾是七时,股和弦的算式;
.根据你发现的规律,分别写出勾是七时,股和弦的算式;科目:czsx 来源: 题型:
| 2 |

| 5 |
| 5 |
| 10 |

| 5 |

科目:czsx 来源:学习周报 数学 华师大八年级版 2009-2010学年 第8期 总第164期 华师大版 题型:044
下面是数学课堂上的一个学习片段,阅读后,请回答下面的问题
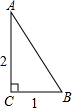
学习了勾股定理的有关内容后,张老师请同学们交流讨论这样一个问题:“已知Rt△ABC的两边长分别为3和4,请你求出第三边长的平方.”
同学们经片刻的思考与交流后,李明同学举手说:“第三边长的平方是25”;王华同学说:“第三边长的平方是7”.还有一些同学也提出了不同的看法
(1)假如你也在课堂上,你的意见如何?为什么?
(2)通过上面数学问题的讨论,你有什么感受?(用一句话表示)
科目:czsx 来源:期末题 题型:解答题
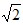 ,它是一个无理数.
,它是一个无理数.
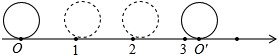
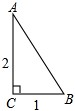
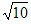 的线段吗?
的线段吗?
 的点吗?
的点吗?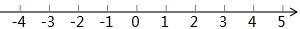
科目:czsx 来源: 题型:解答题
 ,它是一个无理数.
,它是一个无理数.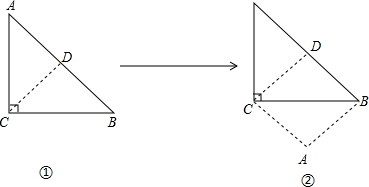
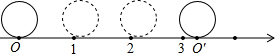
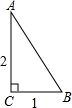
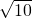 的线段吗?
的线段吗?
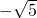 的点吗?
的点吗?
科目:czsx 来源: 题型:
科目:czsx 来源: 题型:
| 7 |
科目:czsx 来源: 题型:
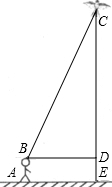 下操作:
下操作:科目:czsx 来源: 题型:阅读理解
| 13 |
| 9 |
| 13 |
| 16 |
| 13 |
| 13 |
| 4 |
| 6 |
| 13 |
| 4 |
| 6 |
| 41 |
| m |
| m |
| m |
| b |
| 2a |
| b |
| 2a |
| 37 |
科目:czsx 来源: 题型:

科目:czsx 来源: 题型:
| 7 |
| A、6 | B、8 | C、35 | D、37 |
科目:czsx 来源: 题型:

科目:czsx 来源: 题型:
科目:czsx 来源: 题型:
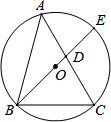 学习了勾股定理的逆定理,我们知道:在一个三角形中,如果两边的平方和等于第三边的平方,那么这个三角形为直角三角形.类似地,我们定义:对于任意的三角形,设其三个角的度数分别为x°、y°和z°,若满足x2+y2=z2,则称这个三角形为勾股三角形.
学习了勾股定理的逆定理,我们知道:在一个三角形中,如果两边的平方和等于第三边的平方,那么这个三角形为直角三角形.类似地,我们定义:对于任意的三角形,设其三个角的度数分别为x°、y°和z°,若满足x2+y2=z2,则称这个三角形为勾股三角形.| 6 |
| 3 |