科目:czsx
来源:2011-2012学年上海市奉贤区九年级调研测试数学试卷(解析版)
题型:解答题
某校开展了以“人生观、价值观”为主题的班队活动,活动结束后,九(2)班数学兴趣小组提出了5个主要观点并在本班50名学生中进行了调查(要求每位同学只选自己最认可的一项观点),并制成了如下扇形统计图.
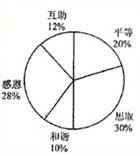
(1)该班学生选择“互助”观点的有
人,在扇形统计图中,“和谐”观点所在扇形区域的圆心角是
度;
(2)如果该校有1500名九年级学生,利用样本估计选择“感恩”观点的九年级学生约有__420____人.
(3)如果数学兴趣小组在这5个主要观点中任选两项观点在全校学生中进行调查,求恰好选到“和谐”和“感恩”观点的概率.(用树状图或列表法分析解答)
查看答案和解析>>
科目:czsx
来源:2012届上海市奉贤区九年级调研测试数学试卷(带解析)
题型:解答题
某校开展了以“人生观、价值观”为主题的班队活动,活动结束后,九(2)班数学兴趣小组提出了5个主要观点并在本班50名学生中进行了调查(要求每位同学只选自己最认可的一项观点),并制成了如下扇形统计图.
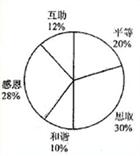
(1)该班学生选择“互助”观点的有 人,在扇形统计图中,“和谐”观点所在扇形区域的圆心角是 度;
(2)如果该校有1500名九年级学生,利用样本估计选择“感恩”观点的九年级学生约有__420____人.
(3)如果数学兴趣小组在这5个主要观点中任选两项观点在全校学生中进行调查,求恰好选到“和谐”和“感恩”观点的概率.(用树状图或列表法分析解答)
查看答案和解析>>
科目:czsx
来源:
题型:

已知:如图,初二•一班数学兴趣小组为了测量河两岸建筑物AB和建筑物CD的水平距离AC,他们首先在A点处测得建筑物CD的顶部D点的仰角为25°,然后爬到建筑物AB的顶部B处测得建筑物CD的顶部D点的俯角为15°30′.已知建筑物AB的高度为30米,求两建筑物的水平距离AC.(精确到0.1米)
查看答案和解析>>
科目:czsx
来源:第28章《锐角三角函数》中考题集(41):28.2 解直角三角形(解析版)
题型:解答题
已知:如图,初二•一班数学兴趣小组为了测量河两岸建筑物AB和建筑物CD的水平距离AC,他们首先在A点处测得建筑物CD的顶部D点的仰角为25°,然后爬到建筑物AB的顶部B处测得建筑物CD的顶部D点的俯角为15°30′.已知建筑物AB的高度为30米,求两建筑物的水平距离AC.(精确到0.1米)

查看答案和解析>>
科目:czsx
来源:第21章《解直角三角形》中考题集(37):21.5 应用举例(解析版)
题型:解答题
已知:如图,初二•一班数学兴趣小组为了测量河两岸建筑物AB和建筑物CD的水平距离AC,他们首先在A点处测得建筑物CD的顶部D点的仰角为25°,然后爬到建筑物AB的顶部B处测得建筑物CD的顶部D点的俯角为15°30′.已知建筑物AB的高度为30米,求两建筑物的水平距离AC.(精确到0.1米)

查看答案和解析>>
科目:czsx
来源:第25章《解直角三角形》中考题集(35):25.3 解直角三角形(解析版)
题型:解答题
已知:如图,初二•一班数学兴趣小组为了测量河两岸建筑物AB和建筑物CD的水平距离AC,他们首先在A点处测得建筑物CD的顶部D点的仰角为25°,然后爬到建筑物AB的顶部B处测得建筑物CD的顶部D点的俯角为15°30′.已知建筑物AB的高度为30米,求两建筑物的水平距离AC.(精确到0.1米)

查看答案和解析>>
科目:czsx
来源:四川省中考真题
题型:解答题
已知:如图,初二·一班数学兴趣小组为了测量河两岸建筑物AB和建筑物CD的水平距离AC,他们首先在A点处测得建筑物CD的顶部D点的仰角为25°,然后爬到建筑物AB的顶部B处测得建筑物CD的顶部D点的俯角为15°30′,已知建筑物AB的高度为30米,求两建筑物的水平距离AC。(精确到0.1米)
查看答案和解析>>
科目:czsx
来源:第4章《锐角三角形》中考题集(35):4.3 解直角三角形及其应用(解析版)
题型:解答题
已知:如图,初二•一班数学兴趣小组为了测量河两岸建筑物AB和建筑物CD的水平距离AC,他们首先在A点处测得建筑物CD的顶部D点的仰角为25°,然后爬到建筑物AB的顶部B处测得建筑物CD的顶部D点的俯角为15°30′.已知建筑物AB的高度为30米,求两建筑物的水平距离AC.(精确到0.1米)

查看答案和解析>>
科目:czsx
来源:第31章《锐角三角函数》中考题集(38):31.3 锐角三角函数的应用(解析版)
题型:解答题
已知:如图,初二•一班数学兴趣小组为了测量河两岸建筑物AB和建筑物CD的水平距离AC,他们首先在A点处测得建筑物CD的顶部D点的仰角为25°,然后爬到建筑物AB的顶部B处测得建筑物CD的顶部D点的俯角为15°30′.已知建筑物AB的高度为30米,求两建筑物的水平距离AC.(精确到0.1米)

查看答案和解析>>
科目:czsx
来源:第1章《解直角三角形》中考题集(39):1.3 解直角三角形(解析版)
题型:解答题
已知:如图,初二•一班数学兴趣小组为了测量河两岸建筑物AB和建筑物CD的水平距离AC,他们首先在A点处测得建筑物CD的顶部D点的仰角为25°,然后爬到建筑物AB的顶部B处测得建筑物CD的顶部D点的俯角为15°30′.已知建筑物AB的高度为30米,求两建筑物的水平距离AC.(精确到0.1米)

查看答案和解析>>
科目:czsx
来源:第7章《锐角三角函数》中考题集(43):7.6 锐角三角函数的简单应用(解析版)
题型:解答题
已知:如图,初二•一班数学兴趣小组为了测量河两岸建筑物AB和建筑物CD的水平距离AC,他们首先在A点处测得建筑物CD的顶部D点的仰角为25°,然后爬到建筑物AB的顶部B处测得建筑物CD的顶部D点的俯角为15°30′.已知建筑物AB的高度为30米,求两建筑物的水平距离AC.(精确到0.1米)

查看答案和解析>>
科目:czsx
来源:第1章《直角三角形的边角关系》中考题集(40):1.5 测量物体的高度(解析版)
题型:解答题
已知:如图,初二•一班数学兴趣小组为了测量河两岸建筑物AB和建筑物CD的水平距离AC,他们首先在A点处测得建筑物CD的顶部D点的仰角为25°,然后爬到建筑物AB的顶部B处测得建筑物CD的顶部D点的俯角为15°30′.已知建筑物AB的高度为30米,求两建筑物的水平距离AC.(精确到0.1米)

查看答案和解析>>
科目:czsx
来源:第25章《解直角三角形》中考题集(35):25.3 解直角三角形及其应用(解析版)
题型:解答题
已知:如图,初二•一班数学兴趣小组为了测量河两岸建筑物AB和建筑物CD的水平距离AC,他们首先在A点处测得建筑物CD的顶部D点的仰角为25°,然后爬到建筑物AB的顶部B处测得建筑物CD的顶部D点的俯角为15°30′.已知建筑物AB的高度为30米,求两建筑物的水平距离AC.(精确到0.1米)

查看答案和解析>>
科目:czsx
来源:
题型:解答题
 已知:如图,初二•一班数学兴趣小组为了测量河两岸建筑物AB和建筑物CD的水平距离AC,他们首先在A点处测得建筑物CD的顶部D点的仰角为25°,然后爬到建筑物AB的顶部B处测得建筑物CD的顶部D点的俯角为15°30′.已知建筑物AB的高度为30米,求两建筑物的水平距离AC.(精确到0.1米)
已知:如图,初二•一班数学兴趣小组为了测量河两岸建筑物AB和建筑物CD的水平距离AC,他们首先在A点处测得建筑物CD的顶部D点的仰角为25°,然后爬到建筑物AB的顶部B处测得建筑物CD的顶部D点的俯角为15°30′.已知建筑物AB的高度为30米,求两建筑物的水平距离AC.(精确到0.1米)
查看答案和解析>>
科目:czsx
来源:第1章《解直角三角形》中考题集(37):1.5 解直角三角形的应用(解析版)
题型:解答题
已知:如图,初二•一班数学兴趣小组为了测量河两岸建筑物AB和建筑物CD的水平距离AC,他们首先在A点处测得建筑物CD的顶部D点的仰角为25°,然后爬到建筑物AB的顶部B处测得建筑物CD的顶部D点的俯角为15°30′.已知建筑物AB的高度为30米,求两建筑物的水平距离AC.(精确到0.1米)

查看答案和解析>>
科目:czsx
来源:2006年四川省乐山市中考数学试卷(课标卷)(解析版)
题型:解答题
(2006•乐山)已知:如图,初二•一班数学兴趣小组为了测量河两岸建筑物AB和建筑物CD的水平距离AC,他们首先在A点处测得建筑物CD的顶部D点的仰角为25°,然后爬到建筑物AB的顶部B处测得建筑物CD的顶部D点的俯角为15°30′.已知建筑物AB的高度为30米,求两建筑物的水平距离AC.(精确到0.1米)

查看答案和解析>>
科目:czsx
来源:
题型:
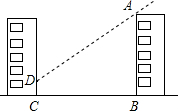
在学习了锐角三角函数相关知识后,九年级(3)班数学兴趣小组的同学利用所学知识测量学校一栋教学楼的高度.如图,他们发现在太阳光下教学楼AB在另一栋楼房留下1.5米高的影子(即图中的CD,两栋楼的底部处于同一水平面),经测量,两楼底部B与C相距21米,同时测得此时太阳光线与地面成35.6°角,请你帮助他们计算教学楼AB的高.(结果精确到0.1米.参考数据:sin35.6°=0.682,cos35.6°=0.813,tan35.6°=0.715)
查看答案和解析>>
科目:czsx
来源:
题型:
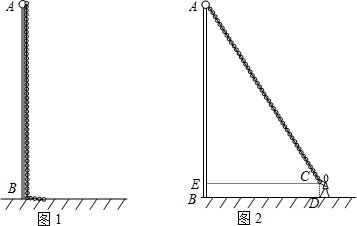
26、学过《勾股定理》后,八年级某班数学兴趣小组来到操场上测量旗杆AB的高度.小华测得从旗杆顶端垂直挂下来的升旗用的绳子比旗杆长1m(如图1),小明拉着绳子的下端往后退,当他将绳子拉直时,小凡测得此时小明拉绳子的手到地面的距离CD为1m,到旗杆的距离CE为8m,(如图2).于是,他们很快算出了旗杆的高度,请你也来试一试.
查看答案和解析>>
科目:czsx
来源:
题型:
我们学习了勾股定理后,都知道“勾三、股四、弦五”.
(1)观察:3,4,5;5,12,13;7,24,25;…,发现这些勾股数的勾都是奇数,且从3起就没有间断过.事实上,勾是三时,股和弦的算式分别是
(9-1),(9+1);勾是五时,股和弦的算式分别是
(25-1),(25+1).根据你发现的规律,分别写出勾是七时,股和弦的算式;
(2)根据(1)的规律,请用含n(n为奇数,且n≥3)的代数式来表示所有这些勾股数的勾、股、弦,合情猜想它们之间的相等关系(请写出两种),并对其中一种猜想加以证明;
(3)继续观察4,3,5;6,8,10;8,15,17;…,可以发现各组的第一个数都是偶数,且从4起也没有间断过.运用类似上述探索的方法,直接用m(m为偶数,且m>4)的代数式来表示股和弦.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
我们学习了勾股定理后,都知道“勾三、股四、弦五”.
(1)观察:3,4,5;5,12,13;7,24,25;…,发现这些勾股数的勾都是奇数,且从3起就没有间断过.事实上,勾是三时,股和弦的算式分别是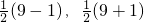 ;勾是五时,股和弦的算式分别是
;勾是五时,股和弦的算式分别是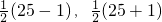 .根据你发现的规律,分别写出勾是七时,股和弦的算式;
.根据你发现的规律,分别写出勾是七时,股和弦的算式;
(2)根据(1)的规律,请用含n(n为奇数,且n≥3)的代数式来表示所有这些勾股数的勾、股、弦,合情猜想它们之间的相等关系(请写出两种),并对其中一种猜想加以证明;
(3)继续观察4,3,5;6,8,10;8,15,17;…,可以发现各组的第一个数都是偶数,且从4起也没有间断过.运用类似上述探索的方法,直接用m(m为偶数,且m>4)的代数式来表示股和弦.
查看答案和解析>>



 已知:如图,初二•一班数学兴趣小组为了测量河两岸建筑物AB和建筑物CD的水平距离AC,他们首先在A点处测得建筑物CD的顶部D点的仰角为25°,然后爬到建筑物AB的顶部B处测得建筑物CD的顶部D点的俯角为15°30′.已知建筑物AB的高度为30米,求两建筑物的水平距离AC.(精确到0.1米)
已知:如图,初二•一班数学兴趣小组为了测量河两岸建筑物AB和建筑物CD的水平距离AC,他们首先在A点处测得建筑物CD的顶部D点的仰角为25°,然后爬到建筑物AB的顶部B处测得建筑物CD的顶部D点的俯角为15°30′.已知建筑物AB的高度为30米,求两建筑物的水平距离AC.(精确到0.1米) 









 已知:如图,初二•一班数学兴趣小组为了测量河两岸建筑物AB和建筑物CD的水平距离AC,他们首先在A点处测得建筑物CD的顶部D点的仰角为25°,然后爬到建筑物AB的顶部B处测得建筑物CD的顶部D点的俯角为15°30′.已知建筑物AB的高度为30米,求两建筑物的水平距离AC.(精确到0.1米)
已知:如图,初二•一班数学兴趣小组为了测量河两岸建筑物AB和建筑物CD的水平距离AC,他们首先在A点处测得建筑物CD的顶部D点的仰角为25°,然后爬到建筑物AB的顶部B处测得建筑物CD的顶部D点的俯角为15°30′.已知建筑物AB的高度为30米,求两建筑物的水平距离AC.(精确到0.1米)

 在学习了锐角三角函数相关知识后,九年级(3)班数学兴趣小组的同学利用所学知识测量学校一栋教学楼的高度.如图,他们发现在太阳光下教学楼AB在另一栋楼房留下1.5米高的影子(即图中的CD,两栋楼的底部处于同一水平面),经测量,两楼底部B与C相距21米,同时测得此时太阳光线与地面成35.6°角,请你帮助他们计算教学楼AB的高.(结果精确到0.1米.参考数据:sin35.6°=0.682,cos35.6°=0.813,tan35.6°=0.715)
在学习了锐角三角函数相关知识后,九年级(3)班数学兴趣小组的同学利用所学知识测量学校一栋教学楼的高度.如图,他们发现在太阳光下教学楼AB在另一栋楼房留下1.5米高的影子(即图中的CD,两栋楼的底部处于同一水平面),经测量,两楼底部B与C相距21米,同时测得此时太阳光线与地面成35.6°角,请你帮助他们计算教学楼AB的高.(结果精确到0.1米.参考数据:sin35.6°=0.682,cos35.6°=0.813,tan35.6°=0.715)
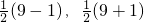 ;勾是五时,股和弦的算式分别是
;勾是五时,股和弦的算式分别是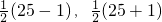 .根据你发现的规律,分别写出勾是七时,股和弦的算式;
.根据你发现的规律,分别写出勾是七时,股和弦的算式;