科目：czsx 来源：初中几何同步单元练习册 第1册 题型：022
已知：如图，A，B，C在一条直线上，且∠1＝∠2．
求证：EB⊥AC．
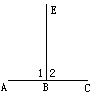
证明：因为 A，B，C在一条直线上( )，
所以∠1＋∠2＝
( )．
因为∠1＝∠2( )，
所以∠1＝∠2＝
所以EB⊥AC( )．
科目：czsx 来源： 题型：
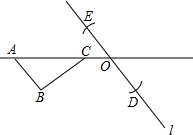已知：如图，A、C、O在同一条直线上，过点O的直线l∥AB．以点O为圆心，AB长为半径画弧，与直线l相交于D、E两点．请利用线段OE或线段OD为一边构造一个三角形，使它和△ABC全等，写出构造方法，并加以证明．科目：czsx 来源： 题型：解答题
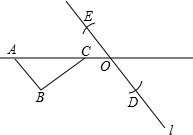已知：如图，A、C、O在同一条直线上，过点O的直线l∥AB．以点O为圆心，AB长为半径画弧，与直线l相交于D、E两点．请利用线段OE或线段OD为一边构造一个三角形，使它和△ABC全等，写出构造方法，并加以证明．科目：czsx 来源：2006-2007学年北京市海淀区九年级（上）期末数学试卷（解析版） 题型：解答题
科目：czsx 来源：2003年河南省中考数学试卷（B卷）（解析版） 题型：填空题
∠BOC+30°，OE平分∠BOC，则∠BOE= 度．
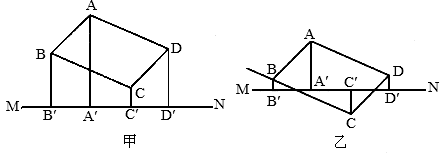
科目：czsx 来源： 题型：044
(1)已知，如图甲，MN是□ABCD外的一条直线，
、
、
、
都垂直于MN，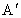
、
、
、
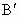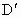为垂足．求证：+
=
+
．
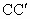(2)若直线MN向上移动，使点C在直线一侧，A、B、D三点在直线另一侧(如图乙)，则垂线段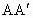
、
、
、
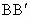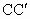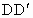之间存在什么关系？先对结论进行猜想，然后加以证明．
科目：czsx 来源： 题型：
如图，点A,D, B,E在同一条直线上，且AD=BE, ∠A=∠FDE,则△ABC≌△DEF.判断这个命题是真命题还是假命题，如果是真命题，请给出证明；如果是假命题请给出一个适当的条件使它成为真命题，并加以证明.
科目：czsx 来源：2012届江西省中等学校招生统一考试数学卷（三） 题型：解答题
如图，点A, D, B,E在同一条直线上，且AD=BE, ∠A=∠FDE,则△ABC≌△DEF.判断这个命题是真命题还是假命题，如果是真命题，请给出证明；如果是假命题请给出一个适当的条件使它成为真命题，并加以证明.
科目：czsx 来源：2012年江西省等学校招生统一考试数学卷（三） 题型：解答题
如图，点A, D, B,E在同一条直线上，且AD=BE, ∠A=∠FDE,则△ABC≌△DEF.判断这个命题是真命题还是假命题，如果是真命题，请给出证明；如果是假命题请给出一个适当的条件使它成为真命题，并加以证明.
科目：czsx 来源： 题型：
科目：czsx 来源：同步题 题型：解答题
（2003•河南）已知：如图，A、O、B在同一条直线上，∠AOC=
已知：如图，A、O、B在同一条直线上，∠AOC=
∠BOC+30°，OE平分∠BOC，则∠BOE=________度．
25、如图，已知A、B、C、D在一条直线上，AB=CD，AE∥DF，BF∥EC，求证：∠E=∠F．
，∠2＝
，则CD与CE的位置关系是________．
