如图,D是等腰直角三角形ABC内一点,BC是斜边答案解析
科目:czsx
来源:
题型:
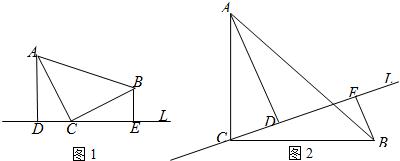
28、如图:已知等腰直角三角形ABC中,∠ACB=90°,直线l经过点C,AD⊥l,BE⊥l,垂足分别为D、E.
(1)证明:△ACD≌△CBE;
(2)如图,当直线l经过△ABC内部时,其他条件不变,这个结论还是真命题吗?如果是真命题,请给出证明;如果是假命题,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
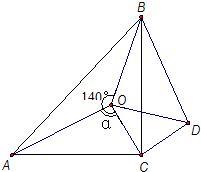
28、如图,点O是等腰直角三角形ABC内一点,∠ACB=90°,∠AOB=140°,∠AOC=α.将△AOC绕直角顶点C按顺时针方向旋转90°得△BDC,连接OD.
(1)试说明△COD是等腰直角三角形;
(2)当α=95°时,试判断△BOD的形状,并说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
若一个三角形经过它的某一顶点的一条直线可把它分成两个小等腰三角形,那么我们称该三角形
为等腰三角形的生成三角形,简称生成三角形.
(1)如图,已知等腰直角三角形ABC,∠A=90度.求证:△ABC是生成三角形;
(2)若等腰三角形ABC有一个内角等于36°,那么请你画出简图说明△ABC是生成三角形;(要求画出直线,标注出图中等腰三角形的顶角、底角的度数.)
(3)说明不同种类(两个三角形各内角度数不会对应相等)的生成三角形有无数多个.
查看答案和解析>>
科目:czsx
来源:
题型:
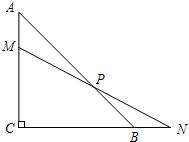
(2006•上海模拟)如图,已知等腰直角三角形ABC中,∠C=90°,AC=2,M是边AC上一点,过点M的直线交CB的延长线于点N,交边AB于点P,且AM=BN.
(1)求证:MP=NP;
(2)设AM=x,四边形MCBP的面积为y,求y与x的函数解析式,并写出函数的定义域;
(3)探索:以线段CM为直径的圆能否与边AB相切?如果能够相切,请求出x的值;如果不能相切,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
19、如图,把一个等腰直角三角形ABC沿斜边上的高BD剪下,与剩下部分能拼成一个平行四边形BCFD(见示意图①)
(1)想一想判断四边形BCFD是平行四边形的依据是
一组对边平行且相等的四边形是平行四边形
.(用平行四边形的判定方法叙述)
(2)做一做按上述方法,请你拼一个与图①位置或形状不同的平行四边形,并在图②中画出示意图.

查看答案和解析>>
科目:czsx
来源:
题型:

如图,已知等腰直角三角形ACB的边AC=BC=a,等腰直角三角形BED的边BE=DE=b,且a<b,点C、B、E放置在一条直线上,连接AD.
(1)求三角形ABD的面积.
(2)如果点P是线段CE的中点,连接AP、DP得到三角形APD,求三角形APD的面积.
(3)(2)中的三角形APD与三角形ABD面积哪个较大?大多少?(结果都可用a、b代数式表示,并化简.)
查看答案和解析>>
科目:czsx
来源:
题型:
24、如图,把一个等腰直角三角形ABC沿斜边上的高CD(裁剪线)剪一刀,从这个三角形中裁下一部分,与剩下部分能拼成一个四边形A′BCD(见示意图1).
(1)猜一猜:四边形A′BCD一定是
平行四边形
形;
(2)试一试:按上述的裁剪方法,请你拼一个与图(1)形状不同的四边形,并在图(2)中画出示意图.

查看答案和解析>>
科目:czsx
来源:2006年上海市部分学校初三数学抽样测试卷(5月份)(解析版)
题型:解答题
如图,已知等腰直角三角形ABC中,∠C=90°,AC=2,M是边AC上一点,过点M的直线交CB的延长线于点N,交边AB于点P,且AM=BN.
(1)求证:MP=NP;
(2)设AM=x,四边形MCBP的面积为y,求y与x的函数解析式,并写出函数的定义域;
(3)探索:以线段CM为直径的圆能否与边AB相切?如果能够相切,请求出x的值;如果不能相切,请说明理由.

查看答案和解析>>
科目:czsx
来源:
题型:解答题
如图,把一个等腰直角三角形ABC沿斜边上的高BD剪下,与剩下部分能拼成一个平行四边形BCFD(见示意图①)
(1)想一想判断四边形BCFD是平行四边形的依据是______.(用平行四边形的判定方法叙述)
(2)做一做按上述方法,请你拼一个与图①位置或形状不同的平行四边形,并在图②中画出示意图.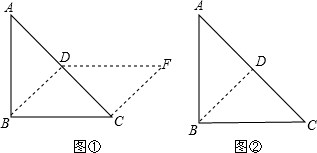
查看答案和解析>>
科目:czsx
来源:
题型:解答题
若一个三角形经过它的某一顶点的一条直线可把它分成两个小等腰三角形,那么我们称该三角形 为等腰三角形的生成三角形,简称生成三角形.
为等腰三角形的生成三角形,简称生成三角形.
(1)如图,已知等腰直角三角形ABC,∠A=90度.求证:△ABC是生成三角形;
(2)若等腰三角形ABC有一个内角等于36°,那么请你画出简图说明△ABC是生成三角形;(要求画出直线,标注出图中等腰三角形的顶角、底角的度数.)
(3)说明不同种类(两个三角形各内角度数不会对应相等)的生成三角形有无数多个.
查看答案和解析>>
科目:czsx
来源:月考题
题型:解答题
若一个三角形经过它的某一顶点的一条直线可把它分成两个小等腰三角形,那么我们称该三角形为等腰三角形的生成三角形,简称生成三角形。
(1)如图,已知等腰直角三角形ABC,∠A=90°,求证:△ABC是生成三角形;
(2) 若等腰三角形ABC有一个内角等于36°,那么请你画出简图说明△ABC是生成三角形;(要求画出直线,标注出图中等腰三角形的顶角、底角的度数。)
(3)说明不同种类(两个三角形各内角度数不会对应相等)的生成三角形有无数多个。
查看答案和解析>>
科目:czsx
来源:2007年中考数学全真模拟试题(10)
题型:044
|
|
如图:把一个等腰直角三角形ABC沿斜边上的高线CD(裁剪线)剪一刀,从这个三角形中剪下一部分,与剩下部分能拼成一个平行四边形ABCD(见示意图a)注意:以下探究过程中有画图要求的,工具不限,不必写画法和证明.
探究一:(1)想一想:判断四边形ABCD是平行四边形的依据是.
(2)做一做:按上述的裁剪方法,请你拼一个与图a位置或形状不同的平行四边形,并在图b中画出示意图.
探究二:在等腰直角三角形ABC中,请你找出其它的裁剪线,把分割成的两部分拼出不同类型的特殊四边形.

| (1) |
|
试一试:你能拼得所有不同类型的特殊四边形有________,它们的裁剪线分别是________.
|
|
(2) |
|
画一画:请在图c中画出一个你拼得的特殊四边形示意图.
|
|
|
查看答案和解析>>
科目:czsx
来源:
题型:解答题
如图:已知等腰直角三角形ABC中,∠ACB=90°,直线l经过点C,AD⊥l,BE⊥l,垂足分别为D、E.
(1)证明:△ACD≌△CBE;
(2)如图,当直线l经过△ABC内部时,其他条件不变,这个结论还是真命题吗?如果是真命题,请给出证明;如果是假命题,请说明理由.
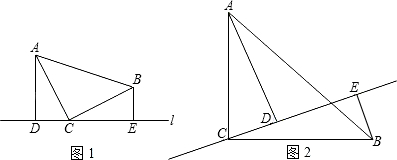
查看答案和解析>>
科目:czsx
来源:2014湘教版八年级上册(专题训练 状元笔记)数学:第2章 三角形 湘教版
题型:044
如图,点O是等腰直角三角形ABC内一点,∠ACB=90°,∠AOB=140°,∠AOC=α.将△AOC绕顶点C按顺时针方向旋转90°得△BDC,连接OD.
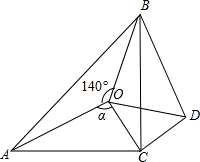
(1)试说明△COD是等腰直角三角形;
(2)当α=95°时,试判断△BOD的形状,并说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
如图,把一个等腰直角三角形ABC沿斜边上的高BD剪下,与剩下部分能拼成一个平行四边形BCFD(见示意图①)
(1)想一想——判断四边形BCFD是平行四边形的依据是
.(用平行四边形的判定方法叙述)
(2)做一做——按上述方法,请你拼一个与图①位置或形状不同的平行四边形,并在图
②中画出示意图.

图① 图②
查看答案和解析>>
科目:czsx
来源:
题型:解答题
如图,把一个等腰直角三角形ABC沿斜边上的高CD(裁剪线)剪一刀,从这个三角形中裁下一部分,与剩下部分能拼成一个四边形A′BCD(见示意图1).
(1)猜一猜:四边形A′BCD一定是________形;
(2)试一试:按上述的裁剪方法,请你拼一个与图(1)形状不同的四边形,并在图(2)中画出示意图.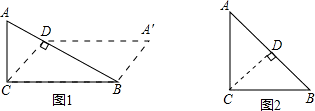
查看答案和解析>>
科目:czsx
来源:
题型:
如图,把一个等腰直角三角形abc沿斜边上的高bd剪下,与剩下部分能拼成一个平行四边形bcfd(见示意图①)
(1)想一想——判断四边形bcfd是平行四边形的依据是
.(用平行四边形的判定方法叙述)
(2)做一做——按上述方法,请你拼一个与图①位置或形状不同的平行四边形,并在图
②中画出示意图.

图① 图②
查看答案和解析>>
科目:czsx
来源:不详
题型:解答题
若一个三角形经过它的某一顶点的一条直线可把它分成两个小等腰三角形,那么我们称该三角形
为等腰三角形的生成三角形,简称生成三角形.
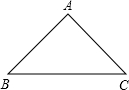
(1)如图,已知等腰直角三角形ABC,∠A=90度.求证:△ABC是生成三角形;
(2)若等腰三角形ABC有一个内角等于36°,那么请你画出简图说明△ABC是生成三角形;(要求画出直线,标注出图中等腰三角形的顶角、底角的度数.)
(3)说明不同种类(两个三角形各内角度数不会对应相等)的生成三角形有无数多个.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
如图,点O是等腰直角三角形ABC内一点,∠ACB=90°,∠AOB=140°,∠AOC=α.将△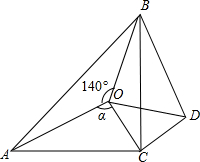 AOC绕直角顶点C按顺时针方向旋转90°得△BDC,连接OD.
AOC绕直角顶点C按顺时针方向旋转90°得△BDC,连接OD.
(1)试说明△COD是等腰直角三角形;
(2)当α=95°时,试判断△BOD的形状,并说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
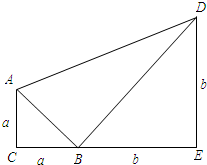 如图,已知等腰直角三角形ACB的边AC=BC=a,等腰直角三角形BED的边BE=DE=b,且a<b,点C、B、E放置在一条直线上,连接AD.
如图,已知等腰直角三角形ACB的边AC=BC=a,等腰直角三角形BED的边BE=DE=b,且a<b,点C、B、E放置在一条直线上,连接AD.
(1)求三角形ABD的面积.
(2)如果点P是线段CE的中点,连接AP、DP得到三角形APD,求三角形APD的面积.
(3)(2)中的三角形APD与三角形ABD面积哪个较大?大多少?(结果都可用a、b代数式表示,并化简.)
查看答案和解析>>


 28、如图,点O是等腰直角三角形ABC内一点,∠ACB=90°,∠AOB=140°,∠AOC=α.将△AOC绕直角顶点C按顺时针方向旋转90°得△BDC,连接OD.
28、如图,点O是等腰直角三角形ABC内一点,∠ACB=90°,∠AOB=140°,∠AOC=α.将△AOC绕直角顶点C按顺时针方向旋转90°得△BDC,连接OD. 为等腰三角形的生成三角形,简称生成三角形.
为等腰三角形的生成三角形,简称生成三角形. (2006•上海模拟)如图,已知等腰直角三角形ABC中,∠C=90°,AC=2,M是边AC上一点,过点M的直线交CB的延长线于点N,交边AB于点P,且AM=BN.
(2006•上海模拟)如图,已知等腰直角三角形ABC中,∠C=90°,AC=2,M是边AC上一点,过点M的直线交CB的延长线于点N,交边AB于点P,且AM=BN.
 如图,已知等腰直角三角形ACB的边AC=BC=a,等腰直角三角形BED的边BE=DE=b,且a<b,点C、B、E放置在一条直线上,连接AD.
如图,已知等腰直角三角形ACB的边AC=BC=a,等腰直角三角形BED的边BE=DE=b,且a<b,点C、B、E放置在一条直线上,连接AD.


 为等腰三角形的生成三角形,简称生成三角形.
为等腰三角形的生成三角形,简称生成三角形.




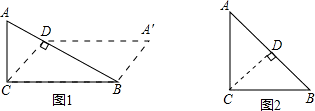



 AOC绕直角顶点C按顺时针方向旋转90°得△BDC,连接OD.
AOC绕直角顶点C按顺时针方向旋转90°得△BDC,连接OD. 如图,已知等腰直角三角形ACB的边AC=BC=a,等腰直角三角形BED的边BE=DE=b,且a<b,点C、B、E放置在一条直线上,连接AD.
如图,已知等腰直角三角形ACB的边AC=BC=a,等腰直角三角形BED的边BE=DE=b,且a<b,点C、B、E放置在一条直线上,连接AD.