如图所示的大桥桥体造型新颖,气势恢宏,两条拱肋如长虹卧波答案解析
科目:czsx
来源:
题型:
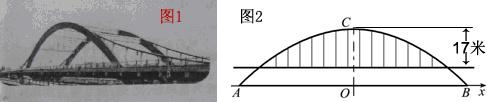
徒骇河大桥是我市第一座特大型桥梁,大桥桥体造型新颖,气势恢宏,两条拱肋如长虹卧波,极具时代气息(如图①).大桥为中承式悬索拱桥,大桥的主拱肋ACB是抛物线的一部分(如图②),跨径AB为100m,拱高OC为25m,抛物线顶点C到桥面的距离为17m.
(1)请建立适当的坐标系,求该抛物线所对应的函数关系式;
(2)七月份汛期来临,河水水位上涨,假设水位比AB所在直线高出1.96m,这时位于水面上的拱肋的跨径是多少?在不计桥面厚度的情况,一条高出水面4.6m的游船是否能够顺利通过大桥?
查看答案和解析>>
科目:czsx
来源:第26章《二次函数》中考题集(21):26.3 实际问题与二次函数(解析版)
题型:解答题
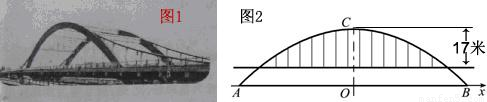
徒骇河大桥是我市第一座特大型桥梁,大桥桥体造型新颖,气势恢宏,两条拱肋如长虹卧波,极具时代气息(如图①).大桥为中承式悬索拱桥,大桥的主拱肋ACB是抛物线的一部分(如图②),跨径AB为100m,拱高OC为25m,抛物线顶点C到桥面的距离为17m.
(1)请建立适当的坐标系,求该抛物线所对应的函数关系式;
(2)七月份汛期来临,河水水位上涨,假设水位比AB所在直线高出1.96m,这时位于水面上的拱肋的跨径是多少?在不计桥面厚度的情况,一条高出水面4.6m的游船是否能够顺利通过大桥?
查看答案和解析>>
科目:czsx
来源:第23章《二次函数与反比例函数》中考题集(21):23.5 二次函数的应用(解析版)
题型:解答题
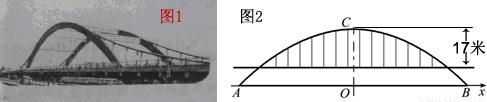
徒骇河大桥是我市第一座特大型桥梁,大桥桥体造型新颖,气势恢宏,两条拱肋如长虹卧波,极具时代气息(如图①).大桥为中承式悬索拱桥,大桥的主拱肋ACB是抛物线的一部分(如图②),跨径AB为100m,拱高OC为25m,抛物线顶点C到桥面的距离为17m.
(1)请建立适当的坐标系,求该抛物线所对应的函数关系式;
(2)七月份汛期来临,河水水位上涨,假设水位比AB所在直线高出1.96m,这时位于水面上的拱肋的跨径是多少?在不计桥面厚度的情况,一条高出水面4.6m的游船是否能够顺利通过大桥?
查看答案和解析>>
科目:czsx
来源:第6章《二次函数》中考题集(23):6.4 二次函数的应用(解析版)
题型:解答题
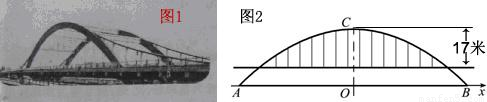
徒骇河大桥是我市第一座特大型桥梁,大桥桥体造型新颖,气势恢宏,两条拱肋如长虹卧波,极具时代气息(如图①).大桥为中承式悬索拱桥,大桥的主拱肋ACB是抛物线的一部分(如图②),跨径AB为100m,拱高OC为25m,抛物线顶点C到桥面的距离为17m.
(1)请建立适当的坐标系,求该抛物线所对应的函数关系式;
(2)七月份汛期来临,河水水位上涨,假设水位比AB所在直线高出1.96m,这时位于水面上的拱肋的跨径是多少?在不计桥面厚度的情况,一条高出水面4.6m的游船是否能够顺利通过大桥?
查看答案和解析>>
科目:czsx
来源:2009年全国中考数学试题汇编《二次函数》(04)(解析版)
题型:解答题
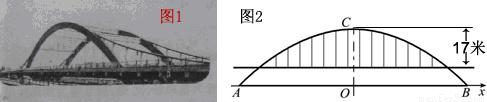
(2009•聊城)徒骇河大桥是我市第一座特大型桥梁,大桥桥体造型新颖,气势恢宏,两条拱肋如长虹卧波,极具时代气息(如图①).大桥为中承式悬索拱桥,大桥的主拱肋ACB是抛物线的一部分(如图②),跨径AB为100m,拱高OC为25m,抛物线顶点C到桥面的距离为17m.
(1)请建立适当的坐标系,求该抛物线所对应的函数关系式;
(2)七月份汛期来临,河水水位上涨,假设水位比AB所在直线高出1.96m,这时位于水面上的拱肋的跨径是多少?在不计桥面厚度的情况,一条高出水面4.6m的游船是否能够顺利通过大桥?
查看答案和解析>>
科目:czsx
来源:第27章《二次函数》中考题集(22):27.3 实践与探索(解析版)
题型:解答题
徒骇河大桥是我市第一座特大型桥梁,大桥桥体造型新颖,气势恢宏,两条拱肋如长虹卧波,极具时代气息(如图①).大桥为中承式悬索拱桥,大桥的主拱肋ACB是抛物线的一部分(如图②),跨径AB为100m,拱高OC为25m,抛物线顶点C到桥面的距离为17m.
(1)请建立适当的坐标系,求该抛物线所对应的函数关系式;
(2)七月份汛期来临,河水水位上涨,假设水位比AB所在直线高出1.96m,这时位于水面上的拱肋的跨径是多少?在不计桥面厚度的情况,一条高出水面4.6m的游船是否能够顺利通过大桥?

查看答案和解析>>
科目:czsx
来源:第34章《二次函数》中考题集(23):34.4 二次函数的应用(解析版)
题型:解答题
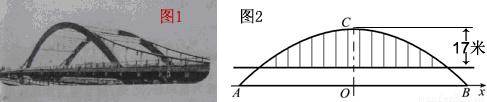
徒骇河大桥是我市第一座特大型桥梁,大桥桥体造型新颖,气势恢宏,两条拱肋如长虹卧波,极具时代气息(如图①).大桥为中承式悬索拱桥,大桥的主拱肋ACB是抛物线的一部分(如图②),跨径AB为100m,拱高OC为25m,抛物线顶点C到桥面的距离为17m.
(1)请建立适当的坐标系,求该抛物线所对应的函数关系式;
(2)七月份汛期来临,河水水位上涨,假设水位比AB所在直线高出1.96m,这时位于水面上的拱肋的跨径是多少?在不计桥面厚度的情况,一条高出水面4.6m的游船是否能够顺利通过大桥?
查看答案和解析>>
科目:czsx
来源:第2章《二次函数》中考题集(24):2.8 二次函数的应用(解析版)
题型:解答题
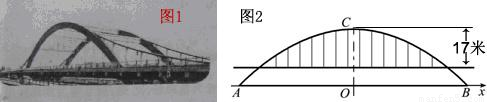
徒骇河大桥是我市第一座特大型桥梁,大桥桥体造型新颖,气势恢宏,两条拱肋如长虹卧波,极具时代气息(如图①).大桥为中承式悬索拱桥,大桥的主拱肋ACB是抛物线的一部分(如图②),跨径AB为100m,拱高OC为25m,抛物线顶点C到桥面的距离为17m.
(1)请建立适当的坐标系,求该抛物线所对应的函数关系式;
(2)七月份汛期来临,河水水位上涨,假设水位比AB所在直线高出1.96m,这时位于水面上的拱肋的跨径是多少?在不计桥面厚度的情况,一条高出水面4.6m的游船是否能够顺利通过大桥?
查看答案和解析>>
科目:czsx
来源:第2章《二次函数》中考题集(21):2.4 二次函数的应用(解析版)
题型:解答题
徒骇河大桥是我市第一座特大型桥梁,大桥桥体造型新颖,气势恢宏,两条拱肋如长虹卧波,极具时代气息(如图①).大桥为中承式悬索拱桥,大桥的主拱肋ACB是抛物线的一部分(如图②),跨径AB为100m,拱高OC为25m,抛物线顶点C到桥面的距离为17m.
(1)请建立适当的坐标系,求该抛物线所对应的函数关系式;
(2)七月份汛期来临,河水水位上涨,假设水位比AB所在直线高出1.96m,这时位于水面上的拱肋的跨径是多少?在不计桥面厚度的情况,一条高出水面4.6m的游船是否能够顺利通过大桥?

查看答案和解析>>
科目:czsx
来源:2009年山东省聊城市中考数学试卷(解析版)
题型:解答题
(2009•聊城)徒骇河大桥是我市第一座特大型桥梁,大桥桥体造型新颖,气势恢宏,两条拱肋如长虹卧波,极具时代气息(如图①).大桥为中承式悬索拱桥,大桥的主拱肋ACB是抛物线的一部分(如图②),跨径AB为100m,拱高OC为25m,抛物线顶点C到桥面的距离为17m.
(1)请建立适当的坐标系,求该抛物线所对应的函数关系式;
(2)七月份汛期来临,河水水位上涨,假设水位比AB所在直线高出1.96m,这时位于水面上的拱肋的跨径是多少?在不计桥面厚度的情况,一条高出水面4.6m的游船是否能够顺利通过大桥?

查看答案和解析>>
科目:czsx
来源:第20章《二次函数和反比例函数》中考题集(20):20.5 二次函数的一些应用(解析版)
题型:解答题
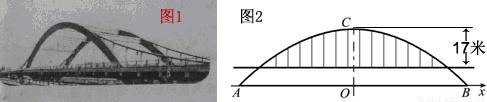
徒骇河大桥是我市第一座特大型桥梁,大桥桥体造型新颖,气势恢宏,两条拱肋如长虹卧波,极具时代气息(如图①).大桥为中承式悬索拱桥,大桥的主拱肋ACB是抛物线的一部分(如图②),跨径AB为100m,拱高OC为25m,抛物线顶点C到桥面的距离为17m.
(1)请建立适当的坐标系,求该抛物线所对应的函数关系式;
(2)七月份汛期来临,河水水位上涨,假设水位比AB所在直线高出1.96m,这时位于水面上的拱肋的跨径是多少?在不计桥面厚度的情况,一条高出水面4.6m的游船是否能够顺利通过大桥?
查看答案和解析>>
科目:czsx
来源:2009年山东省聊城市中考数学试题及答案
题型:044
徒骇河大桥是我市第一座特大型桥梁,大桥桥体造型新颖,气势恢宏,两条拱肋如长虹卧波,极具时代气息(如图①).大桥为中承式悬索拱桥,大桥的主拱肋ACB是抛物线的一部分(如图②),跨径AB为100 m,拱高OC为25 m,抛物线顶点C到桥面的距离为17 m.
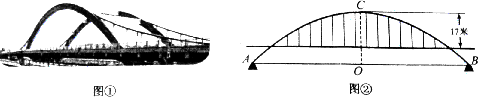
(1)请建立适当的坐标系,求该抛物线所对应的函数关系式;
(2)七月份汛期来临,河水水位上涨,假设水位比AB所在直线高出1.96 m,这时位于水面上的拱肋的跨径是多少?在不计桥面厚度的情况,一条高出水面4.6 m的游船是否能够顺利通过大桥?
查看答案和解析>>
科目:czsx
来源:
题型:解答题
徒骇河大桥是我市第一座特大型桥梁,大桥桥体造型新颖,气势恢宏,两条拱肋如长虹卧波,极具时代气息(如图①).大桥为中承式悬索拱桥,大桥的主拱肋ACB是抛物线的一部分(如图②),跨径AB为100m,拱高OC为25m,抛物线顶点C到桥面的距离为17m.
(1)请建立适当的坐标系,求该抛物线所对应的函数关系式;
(2)七月份汛期来临,河水水位上涨,假设水位比AB所在直线高出1.96m,这时位于水面上的拱肋的跨径是多少?在不计桥面厚度的情况,一条高出水面4.6m的游船是否能够顺利通过大桥?
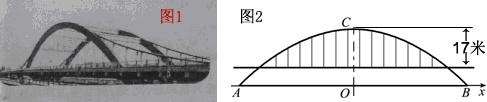
查看答案和解析>>
科目:czsx
来源:
题型:
徒骇河大桥是我市第一座特大型桥梁,大桥桥体造型新颖,气势恢宏,两条拱肋如长虹卧波,极具时代气息(如图①).大桥为中承式悬索拱桥,大桥的主拱肋ACB是抛物线的一部分(如图②),跨径AB为100m,拱高OC为25m,抛物线顶点C到桥面的距离为17m.
(1)请建立适当的坐标系,求该抛物线所对应的函数关系式;
(2)七月份汛期来临,河水水位上涨,假设水位比AB所在直线高出1.96m,这时位于水面上的拱肋的跨径是多少?在不计桥面厚度的情况,一条高出水面4.6m的游船是否能够顺利通过大桥?

查看答案和解析>>
科目:czsx
来源:
题型:013
如图所示的图案中,是轴对称图形且有两条对称轴的是(
)

查看答案和解析>>
科目:czsx
来源:
题型:

如图,用6根一样长的小棒搭成如图所示的图形,试移动AC、BC这两根小棒,使6根小棒组成中心对称的图形.(画出图形)
查看答案和解析>>
科目:czsx
来源:
题型:
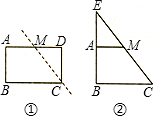
用剪刀将形状如图①所示的矩形纸片ABCD沿着直线CM剪成两部分,其中M为AD的中点.用这两部分纸片可以拼成一些新图形,例如图②中的Rt△BCE就是拼成的一个图形.若利用这两部分纸片拼成的Rt△BCE是等腰直角三角形,设原矩形纸片中的边AB和BC的长分别为a厘米、b厘米,且a、b满足关系式a+b=m-1,ab=m+1,则原矩形纸片的面积是
cm
2.
查看答案和解析>>
科目:czsx
来源:
题型:
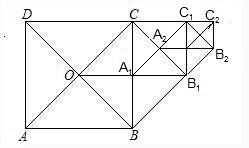
如图所示,在正方形ABCD中,AB=2,两条对角线相交于点O,以OB、OC为邻边作第1个正方形OBB
1C,对角线相交于点A
1;再以A
1B
1、A
1C为邻边作第2个正方形A
1B
1C
1C对角线相交于点O
1;再以O
1B
1、O
1C
1为邻边作第3个正方形O
1B
1B
2C
1,…依此类推.
(1)求第1个正方形OBB
1C的边长a
1和面积S
1;
(2)写出第2个正方形A
1B
1C
1C和第3个正方形的边长a
2,a
3和面积S
2,S
3;
(3)猜想第n个正方形的边长a
n和面积S
n.(不需证明).
查看答案和解析>>
科目:czsx
来源:
题型:

3、如图所示,在△ABC中,CD,BE是两条高,那么图中与∠A相等的角的个数有( )
查看答案和解析>>















 用剪刀将形状如图①所示的矩形纸片ABCD沿着直线CM剪成两部分,其中M为AD的中点.用这两部分纸片可以拼成一些新图形,例如图②中的Rt△BCE就是拼成的一个图形.若利用这两部分纸片拼成的Rt△BCE是等腰直角三角形,设原矩形纸片中的边AB和BC的长分别为a厘米、b厘米,且a、b满足关系式a+b=m-1,ab=m+1,则原矩形纸片的面积是
用剪刀将形状如图①所示的矩形纸片ABCD沿着直线CM剪成两部分,其中M为AD的中点.用这两部分纸片可以拼成一些新图形,例如图②中的Rt△BCE就是拼成的一个图形.若利用这两部分纸片拼成的Rt△BCE是等腰直角三角形,设原矩形纸片中的边AB和BC的长分别为a厘米、b厘米,且a、b满足关系式a+b=m-1,ab=m+1,则原矩形纸片的面积是