科目：czsx 来源：中考必备’04全国中考试题集锦·数学 题型：044
如图，现有两个边长比为1∶2的正方形ABCD与
，已知点B、C、
在同一直线上且点C与点
重合，请你利用这两个正方形，通过截割、平移、旋转的方法，拼出两个相似比为l∶3的三角形
要求：(1)借助原图拼图．
(2)简要说明方法．
(3)指明相似的两个三角形．
科目：czsx 来源：2012年苏教版初中数学九年级上5.4确定圆的条件练习卷（解析版） 题型：选择题
可以作圆，且只可以作一个圆的条件是 _____________．
A．已知圆心 B．已知半径
C．过三个已知点 D．过不在同一直线上的三点
科目：czsx 来源：新教材完全解读 九年级数学 下册(配北师大版新课标) 北师大版新课标 题型：013
可以作圆且只可以作一个圆的条件是
A．已知圆心
B．已知半径
C．过三个已知点
D．过不在同一直线上的三点
科目：czsx 来源： 题型：
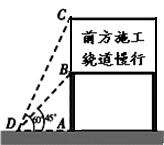因为市区某大型出入口要进行改道施工，有关部门在一个主要路口设立了交通路况指示牌（如图）．已知A、B、C在同一直线上，AC垂直于地面，立杆AB高度是3m，从侧面D点测得指示牌顶端C点和底端B点的仰角分别是60°和45°．求路况指示牌BC的高度（结果保留根号）． 科目：czsx 来源： 题型：
科目：czsx 来源： 题型：
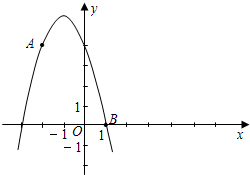
如图,已知点A的坐标为(
,3),AB⊥x轴于B,连接OA,反比例函数
（k >0）的图象与线段OA、AB分别交于点C、D．若AB=3BD,以点C为圆心,CA的
倍的长为半径作圆,则该圆与x轴的位置关系是 ．（填“相离”、“相切”或“相交”）．
科目：czsx 来源： 题型：
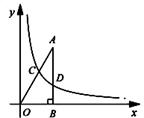
,3),AB⊥x轴于B,连接OA,反比例函数
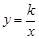（k >0）的图象与线段OA、AB分别交于点C、D．若AB=3BD,以点C为圆心,CA的
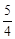倍的长为半径作圆,则该圆与x轴的位置关系是 ．（填“相离”、“相切”或“相交”）．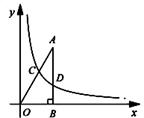
科目：czsx 来源：2010年上海市宝山区中考数学二模试卷（解析版） 题型：解答题
科目：czsx 来源：2013年浙江省鄞州八校中考模拟测试数学试卷（解析版） 题型：填空题
如图,已知点A（0,2）、B（
,2）、C(0,4),过点C向右作平行于x轴的射线,点P是射线上的动点,连结AP,以AP为边在其左侧作等边△APQ ,连结PB、BA.若四边形ABPQ为梯形,则
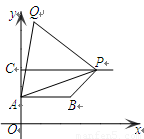
（1）当AB为梯形的底时,点P的横坐标是 ；
（2）当AB为梯形的腰时,点P的横坐标是 .
科目：czsx 来源：2010年江苏省徐州市中考数学模拟试卷（解析版） 题型：解答题
科目：czsx 来源： 题型：
为菱形,求平移后抛物线的表达式；的对称中心点M的坐标． 科目：czsx 来源：2015届山东省文登市七年级下学期期中考试数学试卷（解析版） 题型：解答题
如图已知点C为AB上一点，AC＝12cm，CB＝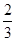
AC，D、E分别为AC、AB的中点，求DE的长。
科目：czsx 来源：2011-2012学年江苏省景德镇市九年级第二次质量检测数学卷（解析版） 题型：解答题
如图,已知点A (-2,4) 和点B (1,0)都在抛物线y=mx2+2mx+n上．
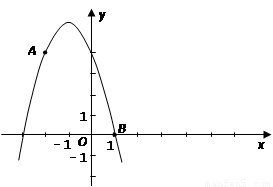
（1）求m、n值；
（2）向右平移上述抛物线,记平移后点A的对应点为A′,点B的对应点为B′,若四边形
为菱形,求平移后抛物线的表达式；
（3）试求出菱形的对称中心点M的坐标．
科目：czsx 来源：2011年初中毕业升学考试（山东莱芜卷）数学 题型：解答题
（本小题满分12分）已知反比例函数
和一次函数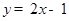
，其中一次
函数图象经过（a，b）与（a+1，b+k）两点.
(1) 求反比例函数的解析式．
(2) 如图,已知点A是第一象限内上述两个函数图象的交点,求A点坐标.
(3) 利用(2)的结果,请问:在X轴上是否存在点P，使△AOP为等腰三角形?若存在，把符合条件的P点坐标都求出来；若不存在，请说明理由．
科目：czsx 来源： 题型：解答题
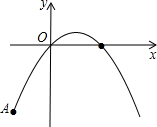如图已知点A（-2，-4），B（2，0），抛物线y=ax2+bx+c过点A、O、B三点．科目：czsx 来源：2012-2013学年山西省七年级第三次月考数学试卷（解析版） 题型：解答题
如图已知点C为AB上一点，AC＝12cm，CB＝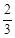
AC，D、E分别为AC、AB的中点，求DE的长。
如图已知点A、B分别在反比例函数y=
读句画图