科目:czsx
来源:
题型:
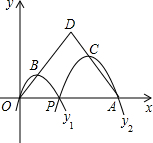
(2012•湖州)如图,已知点A(4,0),O为坐标原点,P是线段OA上任意一点(不含端点O,A),过P、O两点的二次函数y
1和过P、A两点的二次函数y
2的图象开口均向下,它们的顶点分别为B、C,射线OB与AC相交于点D.当OD=AD=3时,这两个二次函数的最大值之和等于( )
查看答案和解析>>
科目:czsx
来源:
题型:阅读理解
(2013•南京二模)阅读材料,回答问题:
如果二次函数y
1的图象的顶点在二次函数y
2的图象上,同时二次函数y
2的图象的顶点在二次函数y
1的图象上,那么我们称y
1的图象与y
2的图象相伴随.
例如:y=(x+1)
2+2图象的顶点(-1,2)在y=-(x+3)
2+6的图象上,同时y=-(x+3)
2+6图象的顶点
(-3,6)也在y=(x+1)
2+2的图象上,这时我们称这两个二次函数的图象相伴随.
(1)说明二次函数y=x
2-2x-3的图象与二次函数y=-x
2+4x-7的图象相伴随;
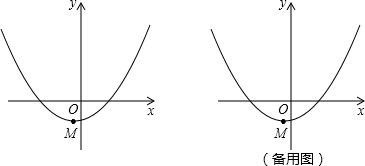
(2)如图,已知二次函数y
1=
(x+1)
2-2图象的顶点为M,点P是x轴上一个动点,将二次函数y
1的图象绕点P旋转180°得到一个新的二次函数y
2的图象,且旋转前后的两个函数图象相伴随,y
2的图象的顶点为N.
①求二次函数y
2的关系式;
②以MN为斜边作等腰直角△MNQ,问y轴上是否存在满足要求的点Q?若存在,求出Q点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
小明在复习数学知识时,针对“求一元二次方程的解”整理了以下几种方法,请你将有关内容补充完整:
例题:求一元二次方程x
2-x-1=0的两个解.
(1)解法一:选择合适的一种方法(公式法、配方法、分解因式法).
(2)解法二:利用二次函数图象与两坐标轴的交点求解.
如图,把方程x
2-x-1=0的解看成是二次函数y=
的图象与x轴交点的横坐标即x
1,x
2就是方程的解.
(3)解法三:利用两个函数图象的交点求解①把方程x
2-x-1=0的解看成是二次函数y=
的图象与一个一次函数y=
的图象交点的横坐标②画出这两个函数的图象,用x
1,x
2在x轴上标出方程的解.
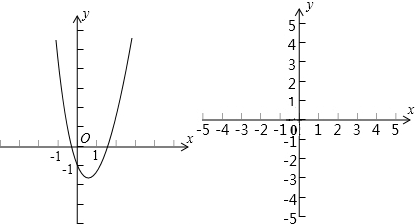
查看答案和解析>>
科目:czsx
来源:
题型:

(2013•锦州)二次函数y=
x2的图象如图,点A
0位于坐标原点,点A
1,A
2,A
3…A
n在y轴的正半轴上,点B
1,B
2,B
3…B
n在二次函数位于第一象限的图象上,点C
1,C
2,C
3…C
n在二次函数位于第二象限的图象上,四边形A
0B
1A
1C
1,四边形A
1B
2A
2C
2,四边形A
2B
3A
3C
3…四边形A
n-1B
nA
nC
n都是菱形,∠A
0B
1A
1=∠A
1B
2A
2=∠A
2B
3A
3…=∠A
n-1B
nA
n=60°,菱形A
n-1B
nA
nC
n的周长为
4n
4n
.
查看答案和解析>>
科目:czsx
来源:
题型:

如图,已知点A(12,0),O为坐标原点,P是线段OA上任意一点(不含端点O,A),过P、O两点的二次函数y
1和过P、A两点的二次函数y
2的图象开口均向下,它们的顶点分别为B、C,射线OB与AC相交于点D.当OD=AD=8时,这两个二次函数的最大值之和等于( )
查看答案和解析>>
科目:czsx
来源:
题型:

如图,已知点A(4,0),O为坐标原点,P是线段OA上任意一点(不含端点O、A),过P、O两点的二次函数y
1和过P、A两点的二次函数y
2的图象开口均向下,它们的顶点分别为B、C,射线OB与AC相交于点D,当OD=AD=3时,这两个二次函数的最大值之和等于
.
查看答案和解析>>
科目:czsx
来源:
题型:
小明在复习数学知识时,针对“求一元二次方程的解”,整理了以下的几种方法,请你按有关内容补充完整:
| 复习日记卡片 |
| 内容:一元二次方程解法归纳 时间:2007年6月×日 |
| 举例:求一元二次方程x2-x-1=0的两个解 |
方法一:选择合适的一种方法(公式法、配方法、分解因式法)求解
解方程:x2-x-1=0.
解: |
方法二:利用二次函数图象与坐标轴的交点求解如图所示,把方程x2-x-1=0的解看成是二次函数y= 的图象与x轴交点的横坐标,即x1,x2就是方程的解.
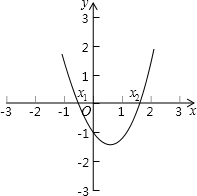 |
方法三:利用两个函数图象的交点求解
(1)把方程x2-x-1=0的解看成是一个二次函数y= 的图象与一个一次函数y= 图象交点的横坐标;
(2)画出这两个函数的图象,用x1,x2在x轴上标出方程的解.
 |
查看答案和解析>>
科目:czsx
来源:2011年江苏省徐州市中考仿真数学试卷(解析版)
题型:解答题
如图,已知二次函数y=

的图象与y轴交于点A,与x轴交于B、C两点,其对称轴与x轴交于点D,连接AC.
(1)点A的坐标为______,点C的坐标为______;
(2)线段AC上是否存在点E,使得△EDC为等腰三角形?若存在,求出所有符合条件的点E的坐标;若不存在,请说明理由;
(3)点P为x轴上方的抛物线上的一个动点,连接PA、PC,若所得△PAC的面积为S,则S取何值时,相应的点P有且只有2个?

查看答案和解析>>
科目:czsx
来源:2013年四川省乐山市沙湾区中考数学调研试卷(解析版)
题型:解答题
如图,二次函数y=
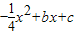
的图象过点A(4,0),B(-4,-4),与y轴交于点C.
(1)证明:∠BAO=∠CAO(其中O是原点);
(2)在抛物线的对称轴上求一点P,使|CP+BP|的值最小;
(3)若E是线段AB上的一个动点(不与A、B重合),过E作y轴的平行线,分别交此二次函数图象及x轴于F、D两点.请问是否存在这样的点E,使DE=2DF?若存在,请求出点E的坐标;若不存在,说明理由.

查看答案和解析>>
科目:czsx
来源:2010年全国中考数学试题汇编《二次函数》(07)(解析版)
题型:解答题
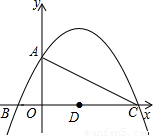
(2010•徐州)如图,已知二次函数y=

的图象与y轴交于点A,与x轴交于B、C两点,其对称轴与x轴交于点D,连接AC.
(1)点A的坐标为______,点C的坐标为______;
(2)线段AC上是否存在点E,使得△EDC为等腰三角形?若存在,求出所有符合条件的点E的坐标;若不存在,请说明理由;
(3)点P为x轴上方的抛物线上的一个动点,连接PA、PC,若所得△PAC的面积为S,则S取何值时,相应的点P有且只有2个?
查看答案和解析>>
科目:czsx
来源:第34章《二次函数》中考题集(29):34.4 二次函数的应用(解析版)
题型:解答题
如图,已知二次函数y=

的图象与y轴交于点A,与x轴交于B、C两点,其对称轴与x轴交于点D,连接AC.
(1)点A的坐标为______,点C的坐标为______;
(2)线段AC上是否存在点E,使得△EDC为等腰三角形?若存在,求出所有符合条件的点E的坐标;若不存在,请说明理由;
(3)点P为x轴上方的抛物线上的一个动点,连接PA、PC,若所得△PAC的面积为S,则S取何

值时,相应的点P有且只有2个?
查看答案和解析>>
科目:czsx
来源:第23章《二次函数与反比例函数》中考题集(26):23.5 二次函数的应用(解析版)
题型:解答题
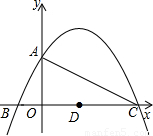
如图,已知二次函数y=
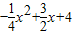
的图象与y轴交于点A,与x轴交于B、C两点,其对称轴与x轴交于点D,连接AC.
(1)点A的坐标为______,点C的坐标为______;
(2)线段AC上是否存在点E,使得△EDC为等腰三角形?若存在,求出所有符合条件的点E的坐标;若不存在,请说明理由;
(3)点P为x轴上方的抛物线上的一个动点,连接PA、PC,若所得△PAC的面积为S,则S取何值时,相应的点P有且只有2个?
查看答案和解析>>
科目:czsx
来源:2013年辽宁省锦州市中考数学试卷(解析版)
题型:填空题

二次函数y=
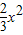
的图象如图,点A
位于坐标原点,点A
1,A
2,A
3…A
n在y轴的正半轴上,点B
1,B
2,B
3…B
n在二次函数位于第一象限的图象上,点C
1,C
2,C
3…C
n在二次函数位于第二象限的图象上,四边形A
B
1A
1C
1,四边形A
1B
2A
2C
2,四边形A
2B
3A
3C
3…四边形A
n-1B
nA
nC
n都是菱形,∠A
B
1A
1=∠A
1B
2A
1=∠A
2B
3A
3…=∠A
n-1B
nA
n=60°,菱形A
n-1B
nA
nC
n的周长为
.
查看答案和解析>>
科目:czsx
来源:2012年湖北省鄂州市三月调考九年级数学试卷(解析版)
题型:解答题
如图,已知二次函数y=

的图象与y轴交于点A,与x轴交于B、C两点,其对称轴与x轴交于点D,连接AC.
(1)点A的坐标为______,点C的坐标为______;
(2)线段AC上是否存在点E,使得△EDC为等腰三角形?若存在,求出所有符合条件的点E的坐标;若不存在,请说明理由;
(3)点P为x轴上方的抛物线上的一个动点,连接PA、PC,若所得△PAC的面积为S,则S取何值时,相应的点P有且只有2个?

查看答案和解析>>
科目:czsx
来源:河北省模拟题
题型:解答题
如图,二次函数y=

的图象与x轴的交点是A(m,0)、B(n,0),与y轴的交点是C(0, 2).
(1)求m、n的值.
(2)设P(x, y)(0< x < n)是抛物线上的动点,过点P作PQ∥y轴交直线BC于点Q.
①线段PQ的长度是否存在最大值?如果存在,最大值是多少?如果不存在,请说明理由
②是否存在这样的点P,使△OAQ为直角三角形?若存在,求出点P的坐标;若不存在,请说明理由。
查看答案和解析>>
科目:czsx
来源:第2章《二次函数》中考题集(26):2.7 最大面积是多少(解析版)
题型:解答题
如图,已知二次函数y=

的图象与y轴交于点A,与x轴交于B、C两点,其对称轴与x轴交于点D,连接AC.
(1)点A的坐标为______,点C的坐标为______;
(2)线段AC上是否存在点E,使得△EDC为等腰三角形?若存在,求出所有符合条件的点E的坐标;若不存在,请说明理由;
(3)点P为x轴上方的抛物线上的一个动点,连接PA、PC,若所得△PAC的面积为S,则S取何

值时,相应的点P有且只有2个?
查看答案和解析>>
科目:czsx
来源:2011年广西柳州市城中区中考数学二模试卷(解析版)
题型:解答题
如图,已知二次函数y=
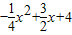
的图象与y轴交于点A,与x轴交于B、C两点,其对称轴与x轴交于点D,连接AC.
(1)点A的坐标为______,点C的坐标为______;
(2)线段AC上是否存在点E,使得△EDC为等腰三角形?若存在,求出所有符合条件的点E的坐标;若不存在,请说明理由;
(3)点P为x轴上方的抛物线上的一个动点,连接PA、PC,若所得△PAC的面积为S,则S取何值时,相应的点P有且只有2个?

查看答案和解析>>
科目:czsx
来源:第2章《二次函数》中考题集(27):2.4 二次函数的应用(解析版)
题型:解答题
如图,已知二次函数y=
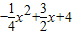
的图象与y轴交于点A,与x轴交于B、C两点,其对称轴与x轴交于点D,连接AC.
(1)点A的坐标为______,点C的坐标为______;
(2)线段AC上是否存在点E,使得△EDC为等腰三角形?若存在,求出所有符合条件的点E的坐标;若不存在,请说明理由;
(3)点P为x轴上方的抛物线上的一个动点,连接PA、PC,若所得△PAC的面积为S,则S取何值时,相应的点P有且只有2个?

查看答案和解析>>
科目:czsx
来源:
题型:解答题
 如图,二次函数y=
如图,二次函数y=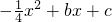 的图象过点A(4,0),B(-4,-4),与y轴交于点C.
的图象过点A(4,0),B(-4,-4),与y轴交于点C.
(1)证明:∠BAO=∠CAO(其中O是原点);
(2)在抛物线的对称轴上求一点P,使|CP+BP|的值最小;
(3)若E是线段AB上的一个动点(不与A、B重合),过E作y轴的平行线,分别交此二次函数图象及x轴于F、D两点.请问是否存在这样的点E,使DE=2DF?若存在,请求出点E的坐标;若不存在,说明理由.
查看答案和解析>>
科目:czsx
来源:2010年江苏省徐州市中考数学试卷(解析版)
题型:解答题
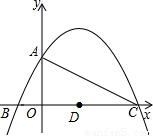
(2010•徐州)如图,已知二次函数y=

的图象与y轴交于点A,与x轴交于B、C两点,其对称轴与x轴交于点D,连接AC.
(1)点A的坐标为______,点C的坐标为______;
(2)线段AC上是否存在点E,使得△EDC为等腰三角形?若存在,求出所有符合条件的点E的坐标;若不存在,请说明理由;
(3)点P为x轴上方的抛物线上的一个动点,连接PA、PC,若所得△PAC的面积为S,则S取何值时,相应的点P有且只有2个?
查看答案和解析>>

 (2012•湖州)如图,已知点A(4,0),O为坐标原点,P是线段OA上任意一点(不含端点O,A),过P、O两点的二次函数y1和过P、A两点的二次函数y2的图象开口均向下,它们的顶点分别为B、C,射线OB与AC相交于点D.当OD=AD=3时,这两个二次函数的最大值之和等于( )
(2012•湖州)如图,已知点A(4,0),O为坐标原点,P是线段OA上任意一点(不含端点O,A),过P、O两点的二次函数y1和过P、A两点的二次函数y2的图象开口均向下,它们的顶点分别为B、C,射线OB与AC相交于点D.当OD=AD=3时,这两个二次函数的最大值之和等于( )
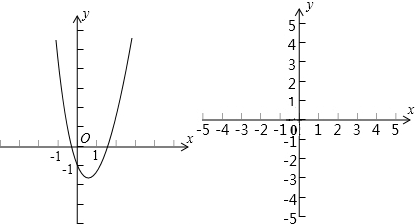
 (2013•锦州)二次函数y=
(2013•锦州)二次函数y= 如图,已知点A(12,0),O为坐标原点,P是线段OA上任意一点(不含端点O,A),过P、O两点的二次函数y1和过P、A两点的二次函数y2的图象开口均向下,它们的顶点分别为B、C,射线OB与AC相交于点D.当OD=AD=8时,这两个二次函数的最大值之和等于( )
如图,已知点A(12,0),O为坐标原点,P是线段OA上任意一点(不含端点O,A),过P、O两点的二次函数y1和过P、A两点的二次函数y2的图象开口均向下,它们的顶点分别为B、C,射线OB与AC相交于点D.当OD=AD=8时,这两个二次函数的最大值之和等于( ) 如图,已知点A(4,0),O为坐标原点,P是线段OA上任意一点(不含端点O、A),过P、O两点的二次函数y1和过P、A两点的二次函数y2的图象开口均向下,它们的顶点分别为B、C,射线OB与AC相交于点D,当OD=AD=3时,这两个二次函数的最大值之和等于
如图,已知点A(4,0),O为坐标原点,P是线段OA上任意一点(不含端点O、A),过P、O两点的二次函数y1和过P、A两点的二次函数y2的图象开口均向下,它们的顶点分别为B、C,射线OB与AC相交于点D,当OD=AD=3时,这两个二次函数的最大值之和等于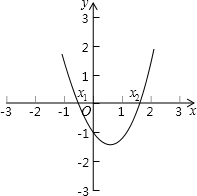
 的图象与y轴交于点A,与x轴交于B、C两点,其对称轴与x轴交于点D,连接AC.
的图象与y轴交于点A,与x轴交于B、C两点,其对称轴与x轴交于点D,连接AC.
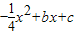 的图象过点A(4,0),B(-4,-4),与y轴交于点C.
的图象过点A(4,0),B(-4,-4),与y轴交于点C.
 的图象与y轴交于点A,与x轴交于B、C两点,其对称轴与x轴交于点D,连接AC.
的图象与y轴交于点A,与x轴交于B、C两点,其对称轴与x轴交于点D,连接AC.
 的图象与y轴交于点A,与x轴交于B、C两点,其对称轴与x轴交于点D,连接AC.
的图象与y轴交于点A,与x轴交于B、C两点,其对称轴与x轴交于点D,连接AC. 值时,相应的点P有且只有2个?
值时,相应的点P有且只有2个?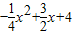 的图象与y轴交于点A,与x轴交于B、C两点,其对称轴与x轴交于点D,连接AC.
的图象与y轴交于点A,与x轴交于B、C两点,其对称轴与x轴交于点D,连接AC.
 二次函数y=
二次函数y=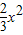 的图象如图,点A位于坐标原点,点A1,A2,A3…An在y轴的正半轴上,点B1,B2,B3…Bn在二次函数位于第一象限的图象上,点C1,C2,C3…Cn在二次函数位于第二象限的图象上,四边形AB1A1C1,四边形A1B2A2C2,四边形A2B3A3C3…四边形An-1BnAnCn都是菱形,∠AB1A1=∠A1B2A1=∠A2B3A3…=∠An-1BnAn=60°,菱形An-1BnAnCn的周长为 .
的图象如图,点A位于坐标原点,点A1,A2,A3…An在y轴的正半轴上,点B1,B2,B3…Bn在二次函数位于第一象限的图象上,点C1,C2,C3…Cn在二次函数位于第二象限的图象上,四边形AB1A1C1,四边形A1B2A2C2,四边形A2B3A3C3…四边形An-1BnAnCn都是菱形,∠AB1A1=∠A1B2A1=∠A2B3A3…=∠An-1BnAn=60°,菱形An-1BnAnCn的周长为 .  的图象与y轴交于点A,与x轴交于B、C两点,其对称轴与x轴交于点D,连接AC.
的图象与y轴交于点A,与x轴交于B、C两点,其对称轴与x轴交于点D,连接AC.
 的图象与x轴的交点是A(m,0)、B(n,0),与y轴的交点是C(0, 2).
的图象与x轴的交点是A(m,0)、B(n,0),与y轴的交点是C(0, 2).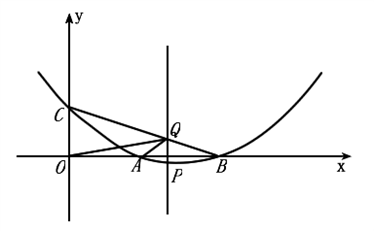
 的图象与y轴交于点A,与x轴交于B、C两点,其对称轴与x轴交于点D,连接AC.
的图象与y轴交于点A,与x轴交于B、C两点,其对称轴与x轴交于点D,连接AC. 值时,相应的点P有且只有2个?
值时,相应的点P有且只有2个?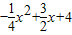 的图象与y轴交于点A,与x轴交于B、C两点,其对称轴与x轴交于点D,连接AC.
的图象与y轴交于点A,与x轴交于B、C两点,其对称轴与x轴交于点D,连接AC.
 的图象与y轴交于点A,与x轴交于B、C两点,其对称轴与x轴交于点D,连接AC.
的图象与y轴交于点A,与x轴交于B、C两点,其对称轴与x轴交于点D,连接AC.
 如图,二次函数y=
如图,二次函数y=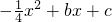 的图象过点A(4,0),B(-4,-4),与y轴交于点C.
的图象过点A(4,0),B(-4,-4),与y轴交于点C. 的图象与y轴交于点A,与x轴交于B、C两点,其对称轴与x轴交于点D,连接AC.
的图象与y轴交于点A,与x轴交于B、C两点,其对称轴与x轴交于点D,连接AC.