
科目:czsx 来源: 题型:

科目:czsx 来源:2011年初中毕业升学考试(贵州六盘水卷)数学 题型:解答题
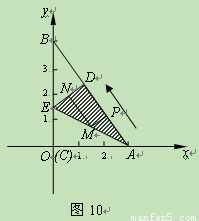
(2011贵州六盘水,25,16分)如图10所示,Rt△ABC是一张放在平面直角坐标系中的纸片,点C与原点O重合,点A在x轴的正半轴上,点B在y轴的正半轴上,已知OA=3,OB=4。将纸片的直角部分翻折,使点C落在AB边上,记为D点,AE为折痕,E在y轴上。
(1)在图10所示的直角坐标系中,求E点的坐标及AE的长。
(2)线段AD上有一动点P(不与A、D重合)自A点沿AD方向以每秒1个单位长度向D点作匀速运动,设运动时间为t秒(0<t<3),过P点作PM∥DE交AE于M点,过点M作MN∥AD交DE于N点,求四边形PMND的面积S与时间t之间的函数关系式,当t取何值时,S有最大值?最大值是多少?
(3)当t(0<t<3)为何值时,A、D、M三点构成等腰三角形?并求出点M的坐标。
科目:czsx 来源: 题型:
(2011贵州六盘水,25,16分)如图10所示,Rt△ABC是一张放在平面直角坐标系中的纸片,点C与原点O重合,点A在x轴的正半轴上,点B在y轴的正半轴上,已知OA=3,OB=4。将纸片的直角部分翻折,使点C落在AB边上,记为D点,AE为折痕,E在y轴上。
(1)在图10所示的直角坐标系中,求E点的坐标及AE的长。
(2)线段AD上有一动点P(不与A、D重合)自A点沿AD方向以每秒1个单位长度向D点作匀速运动,设运动时间为t秒(0<t<3),过P点作PM∥DE交AE于M点,过点M作MN∥AD交DE于N点,求四边形PMND的面积S与时间t之间的函数关系式,当t取何值时,S有最大值?最大值是多少?
(3)当t(0<t<3)为何值时,A、D、M三点构成等腰三角形?并求出点M的坐标。
科目:czsx 来源:2011-2012年山东省济宁地区七年级第一学期期中考试数学卷 题型:解答题
(本题满分6分)如图,在B港有甲乙两艘渔船,若甲船沿北偏东50方向以每小时8海里的速度前进,乙船沿南偏东某方向以每小时15 海里的速度前行,1小时后,甲船到M岛,乙船到P岛,两岛相距17海里,你能知道乙船沿哪个方向航行吗?

科目:czsx 来源:2011-2012年山东省济宁地区七年级第一学期期中考试数学卷 题型:解答题
(本题满分6分)如图,△ABC中,∠ABC与∠ACB的平分线相交于F,过F作DE∥BC交AB于D,交AC于E,若BD+CE=9,求线段DE的长.

科目:czsx 来源: 题型:
(本题满分9分)如图,在![]() 中,
中,![]() ,
,![]() ,把边长分别为
,把边长分别为![]() 的
的![]() 个正方形依次放入
个正方形依次放入![]() 中,请回答下列问题:
中,请回答下列问题:
(1)按要求填表
(2)第![]() 个正方形的边长
个正方形的边长![]() ;
;
(3)若![]() 是正整数,且
是正整数,且![]() ,试判断
,试判断![]() 的关系.
的关系.
科目:czsx 来源:2012届云南省西盟佤族自治县九年级上学期期末考试数学卷 题型:选择题
(本题满分8分)如图,AB是⊙O的直径,弦CD⊥AB于点E,∠CDB=30º,
⊙O的半径为 cm,求弦CD的长.
cm,求弦CD的长.
 |
科目:czsx 来源:2012届江苏省苏州市相城实验中学九年级10月月考数学卷 题型:解答题
(本题满分6分)如图,以等腰三角形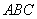 的一腰
的一腰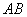 为直径的⊙O交底边
为直径的⊙O交底边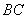 于点
于点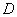 ,交
,交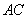 于点
于点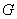 ,连结
,连结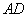 ,并过点
,并过点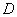 作
作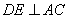 ,垂足为
,垂足为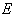 .根据以上条件写出三个正确结论(除
.根据以上条件写出三个正确结论(除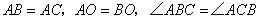 外)是:
外)是:
(1)________________;(2)________________;(3)________________.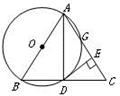
科目:czsx 来源: 题型:
 中,E,F分别为边AB,CD的中点,连接DE,BF,BD.
中,E,F分别为边AB,CD的中点,连接DE,BF,BD.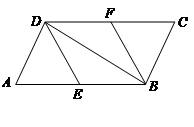
科目:czsx 来源:2011-2012年山东省东营市胜利油田九年级上学期期末考试数学卷 题型:解答题
(本题满分7分)如图,热气球的探测器显示,从热气球看一栋高楼的顶部B的仰角为45°,看这栋高楼底部C的俯角为60°,热气球与高楼的水平距离AD为50m,求这栋楼的高度.( 取1.414,
取1.414, 取1.732)
取1.732)

科目:czsx 来源:2011-2012年山东省教研片八年级上学期期中质量检查数学卷 题型:解答题
(本题满分6分)
如图所示,已知点A、B、C、D在同一条直线上,AM=CN,BM=DN,∠M=∠N,求证:AC=BD。
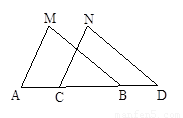
科目:czsx 来源:2011年初中毕业升学考试(贵州铜仁卷)数学 题型:解答题
(本题满分12分)如图,在边长为2的正方形ABCD中,P为AB的中点,Q为边CD上一动点,设DQ=t(0≤t≤2),线段PQ的垂直平分线分别交边AD、BC于点M、N,过Q作QE⊥AB于点E,过M作MF⊥BC于点F.
(1)当t≠1时,求证:△PEQ≌△NFM;
(2)顺次连接P、M、Q、N,设四边形PMQN的面积为S,求出S与自变量t之间的函数关系式,并求S的最小值.
 |
科目:czsx 来源: 题型:
(本题满分7分)如图,已知一次函数y=kx+b的图象与反比例函数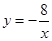
的图象交于A、B两点,且点A的横坐标和点B的纵坐标都是-2.
求:(1)一次函数的解析式;
(2)△ABC的面积.
科目:czsx 来源:2011年湖北省荆州市芦陵中学中考模拟试题(二)数学卷 题型:解答题
(本题满分7分)如图,四边形ABCD是菱形,点G是BC延长线上一点,连接AG,分别交BD、CD于点E、F,连接CE.
(1)求证:∠DAE=∠DCE;
(2)当AE=2EF时,判断FG与EF有何等量关系?并证明你的结论?
科目:czsx 来源:2010年湖北省黄冈市初一上学期期末模拟数学卷 题型:解答题
(本题满分12分)
如图,在△ABC中,AD平分∠BAC. 
(1)若AC=BC,∠B︰∠C=2︰1,试写出图中的所有等腰三角形,并给予证明.
(2)若AB BD=AC,求∠B︰∠C 的比值
BD=AC,求∠B︰∠C 的比值
科目:czsx 来源: 题型:
(本题满分13分)如图,在梯形ABCD中,AD∥BC,∠B=90°,BC=6,AD=3,∠DCB=30°.点E、F同时从B点出发,沿射线BC向右匀速移动.已知F点移动速度是E点移动速度的2倍,以EF为一边在CB的上方作等边△EFG.设E点移动距离为x(x>0).
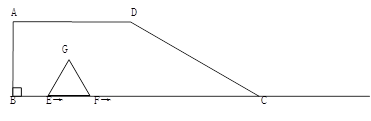
⑴△EFG的边长是____(用含有x的代数式表示),当x=2时,点G的位置在_______;
⑵若△EFG与梯形ABCD重叠部分面积是y,求
①当0<x≤2时,y与x之间的函数关系式;
②当2<x≤6时,y与x之间的函数关系式;
⑶探求⑵中得到的函数y在x取含何值时,存在最大值,并求出最大值.
科目:czsx 来源: 题型:
(本题满分12分)如图1,△ABC的边BC在直线上,AC⊥BC,且AC=BC;△EFP的边FP也在直线
上,边EF与边AC重合,且EF=FP.
1.(1)将△EFP沿直线向左平移到图2的位置时,EP交AC于点Q,连结AP,BQ.猜想并写出BQ与AP所满足的数量关系,请证明你的猜想;
2.(2)将△EFP沿直线向左平移到图3的位置时,EP的延长线交AC的延长线于点Q,连结AP,BQ.你认为(1)中所猜想的BQ与AP的数量关系还成立吗?若成立,给出证明;若不成立,请说明理由;
3.(3)若AC=BC=4,设△EFP平移的距离为x,当0≤x≤8时,△EFP与△ABC重叠部分的面积为S,请写出S与x之间的函数关系式,并求出最大值.