科目：gzsx 来源：2010-2011学年河南省长葛市高三上学期期中考试数学理卷 题型：解答题
(本小题满分12分)设函数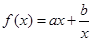
，曲线
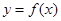在点M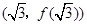
处的切线方程为
．
（Ⅰ）求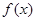
的解析式；
（Ⅱ）求函数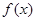的单调递减区间；
（Ⅲ）证明：曲线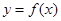上任一点处的切线与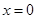直线
和直线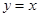
所围成的三角形面积为定值，并求此定值．
科目：gzsx 来源： 题型：
(2009山东卷理)(本小题满分12分)设函数f(x)=cos(2x+
)+sin
x.
(1) 求函数f(x)的最大值和最小正周期.
(2) 设A,B,C为
ABC的三个内角，若cosB=
，
，且C为锐角，求sinA.
科目：gzsx 来源：辽宁省沈阳二中2010-2011学年高二下学期期末考试数学（文） 题型：解答题
(本小题满分12分)若函数y＝lg(3－4x＋x2)的定义域为M.当x∈M时，求f(x)＝2x＋2－3×4x的最值及相应的x的值．
科目：gzsx 来源：2010-2011学年广东省高三下学期二轮复习数学理卷 题型：解答题
（本小题满分12分）
已知曲线
在点
处的切线斜率为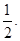
（Ⅰ）求
的极值；
（Ⅱ）设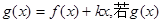
在（一∞，1）上是增函数，求实数
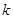的取值范围；
科目：gzsx 来源：辽宁省2012届高二下学期期末考试数学（文） 题型：解答题
(本小题满分12分)若函数y＝lg(3－4x＋x2)的定义域为M.当x∈M时，求f(x)＝2x＋2－3×4x的最值及相应的x的值．
科目：gzsx 来源：2010年河南省辉县市高一上学期第二次阶段性考试数学卷 题型：解答题
（本小题满分12分）
函数
是定义域在（－1，1）上的奇函数，且
.
（1）确定函数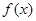
的解析式；
（2）用定义证明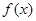在（－1，1）上是增函数；
（3）解不等式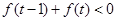
.
科目：gzsx 来源： 题型：
（本小题满分12分）
已知曲线
在点
处的切线与x轴的交点的横坐标为
（1）求数列
的通项公式；
（2）设
，数列
的前n项和为
对所有
都成立的最小正整数m的值。
科目：gzsx 来源：辽宁省沈阳二中2010-2011学年高二下学期期末考试数学（文） 题型：解答题
(本小题满分12分)设函数f（x）=
（x＞0且x≠1）.
（1）求函数f（x）的单调区间；
（2）已知2
＞xa对任意x∈（0，1）成立，求实数a的取值范围.
科目：gzsx 来源：2010-2011学年江苏省苏州市高三摸底考试数学卷 题型：解答题
(本小题满分12分)设函数
(其中
)的图象在
处的切线与直线
平行.
(1)求
的值；
(2)求函数
在区间[0,1]的最小值；
(3)若
,
,
,且
,
试根据上述(Ⅰ)、(Ⅱ)的结论证明:
.
科目：gzsx 来源：辽宁省2012届高二下学期期末考试数学（文） 题型：解答题
(本小题满分12分)设函数f（x）=
（x＞0且x≠1）.
（1）求函数f（x）的单调区间；
（2）已知2
＞xa对任意x∈（0，1）成立，求实数a的取值范围.
科目：gzsx 来源：2010-2011学年宁夏高三第一次月考文科数学卷 题型：解答题
(本小题满分12分)
设函数
，已知
是奇函数.
（Ⅰ）求
、
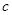的值；
（Ⅱ）求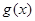
的单调区间与极值.
科目：gzsx 来源：2010-2011学年新疆农七师高级中学高三第二次模拟考试数学文卷 题型：解答题
( (本小题满分12分)
设函数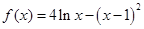
．
（Ⅰ）求函数
的单调递增区间；
（Ⅱ）若关于
的方程
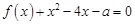在区间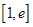
内恰有两个相异的实根，求实数
的取值范围．
科目：gzsx 来源：2010-2011年山东省莘县实验高中高二模块考试文科数学试题 题型：解答题
( 本小题满分12分)
设
函数
在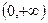
上单调递减;
曲线
与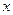
轴交于不同的两点．如果
且
为假命题，或为真命题，求a的取值范围．
科目：gzsx 来源：2010-2011学年山东省重点中学高二下学期期末考试数学（文） 题型：解答题
(本小题满分12分)
设函数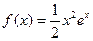
．
⑴求函数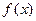
的单调区间；
⑵若当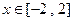
时，不等式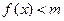
恒成立，求实数
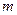的取值范围．
科目：gzsx 来源：2010-2011年山东省高二模块考试文科数学试题 题型：解答题
( 本小题满分12分)
设
函数
在
上单调递减;
曲线
与
轴交于不同的两点．如果
且
为假命题，或为真命题，求a的取值范围．
科目：gzsx 来源：2007年普通高等学校招生全国统一考试理科数学卷（陕西） 题型：解答题
(本小题满分12分)
设函数f(x)=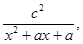
其中a为实数.
(Ⅰ)若f(x)的定义域为R,求a的取值范围;
(Ⅱ)当f(x)的定义域为R时，求f(x)的单减区间.
若对于任意
都有
成立, 求实数
的取值范围.
的定义域为集合
，不等式
的解集为集合
．
，
．
的单调区间；
对任意
成立，求实数
的取值范围