科目：gzyw 来源：高一语试卷 题型：013
阅读下文，回答下列题
我们再从技术的角度研究确定边界。定义是条约谈判者的工作。它是口头和概念方面的，它要确定或相对确定使用的地理术语和被提到的地方的名称等。但是，这与领土的实际之间有着非常明显的距离。如果事情到此①为止，那么，边界就不会有任何实际意义。定界是在大比例尺的地图上工作，今天是在航空摄影照片上工作。要为根据作为文件的地图提供一张尽可能准确详尽的边界绘图，这是地图绘制者的工作。在土地现场进行划界使地图和领土、“绘制的”和“呈现的”相吻合，[当没有可能使边界依托于起伏的地面或者地形中断时，划界可能通过一些界标、墙、篱、石头砌成的线，也就是一些简陋的建筑物或自然景物中的标记落实。]②应该恰当地指出，不管怎样，确定一条边界需要时间，可能要很长的时间。[边界上，比如在非洲，许多边界只是定了界限；划界却没有进行。]美国和加拿大的边界是在1792至1925年之间确定的。法兰西和西班牙在比利牛斯山的边界从11世纪起实际上就封锁起来了，直到19世纪后半叶才划定了界限。③[划定边界，它能获得相当可观的，有时是无法估计的资料，使国家有可能准确地了解它们的主权延伸的面积，同时消除不肯定的边界走向的冲突根源。这种资料的获得代价昂贵，因为划界工作可能延长并遇到困难，从而成为后期工作经常拖延的原因。然而，划界作为秩序稳定的因素又是不可缺少的。]很明显，这是有关陆地上边界的，而设想为海域划界就更困难了，更不必说空中的边界了。我们有理由问一下，为什么要在边界的确定上花这么大的力气呢？对这个问题回答比较简单：由于有一条边界的准确走向，边界显然会更容易和更有效地去履行它的职能。[边界或功能是由它与人和事的关系来确定的。]其机动性受到边界功能的控制、限制或者被完全排除。边界是一种真正的工具。人们把它归入由各种政治集团支配的那一类。就法律而言，人们要考虑到在确定的边界内，实际上在勘定的边界线内的领土上，一整套司法机构具有优势。在这个领土之内，一个国家可以行使它的人为法。通过对外国产品征收税来保护国内市场，为国家财政预算提供资金，起一种基本经济政策的作用，这个财政功能无疑常常是消极的。对人和物通过边界时进行检查：管制移民活动，检查资金和财产，任何管制都是执行来自经济、社会和文化政策的那些准则。我们还需要提一提，在今天仅在与常规武器发生关系时才有意义的军事功能以及体现在“墙”“铁幕”和“竹幕”等方向的意识形态功能，它把边界变为帝国的界限，它不仅区分两块领土，也区分了两种“时间节奏”、两类时空组织。[政治地理学在边界问题上曾经经历过多次分类，一些过分简单的分类把它们区别为天然边界和人为边界；另外一些分类则更精细，像博格斯和哈茨霍恩的分类。博格斯分类是地貌学的仔细描述的分类。在外貌性的类型中，边界依赖于山岭、分水线、沙漠、河流等，法兰西——西班牙边界，在某种程度上，在某些地段就符合这种类型。在阿尔卑斯山的法兰西——意大利边界也是如此，但是在那里也并不是始终都实行了自然地理原则。在墨西哥湾的埃尔帕索的美利坚——墨西哥边界与格朗德河相吻合，但余下部分却转而成为一种几何类型。几何类型的边界是根据天文学的尺度、由子午线、纬线、弧线或恒向线来决定的。足以说明这种类型边界的最古老的一个例子无疑就是对新大陆的瓜分。这就是亚历山大6世在1463年答应把位于亚速尔群岛一个岛屿以西100海里的领土交给西班牙；不久之后，鉴于葡萄牙的反应，重新进行瓜分，并根据托德西亚条约作了修改。非洲的许多边界属于几何类型，完全不符合人类、种族、语言和部族的现实。几何型边界从表面上看虽然简单，但勘定边界线时却很不方便。人类地理类型是根据某些文化、种族、语言、宗教等标准来划界的。这类边界特别依赖于民族原则。这种类型的边界，一般来说，对于这些集体有利，因为它有助于尊重他们的统一，但是，它并不如人们想像的那样常见。剩下的是多种因素结合的复杂类型。在确定边界时要把这些因素同时加以考虑。欧洲的许多边界都是这种复杂类型。沿着一条相当重要的边界可能会有几种类型，“纯粹”类型的边界毕竟很少。在这个意义上说，博格斯的分类虽然有用，却难于掌握。哈茨霍恩的遗传分类，企图在边界和人类占有之间找出一种关系。他的原则是要知道这条边界究竟是在当地居民把人类环境的主要因素安排停当之前、之中、还是之后确定下来的。运用这个原则，人们可以分辨出先成边界，如美利坚——加拿大边界，大多数欧洲边界一类的后成边界，以及以色列边界那样的强加边境。作战线和停火线往往属于强加类型，而先成边界和后成边界分别具有按其居民来说的“青年”地区和“老年”地区这个特点。这些分类不是追加的，恰恰相反，它们是必要的补充，而且它们甚至可能结合起来并作些交叉。可能有一种表达边界现象的地理历史手段。这就是说，这些分类总之是太老了，在相当大的程度上已不能适应边界的现代观念，而这些观念是今天某些人文科学所需要的④。]（《边界的构成要素》）
1．①“此”的指代对象是
[ ]
A．从技术角度研究确定边界。
B．确定使用的地理术语和被提到的地方名称。
C．领土实际之间有非常明显的距离。
D．以上三项。
2．②下面是方括号内的语句的缩写，较准确地保留句意的一句是
[ ]
A．没有可能依托或中断时，划界通过线落实。
B．划界可能通过线落实。
C．划界可能落实。
D．划界落实。
3．③从此处上溯到开头这段文字说明了以下哪一组问题？
[ ]
A．确定名称 实地测绘 现场落实
B．概念 绘图 标记
C．口头和概念 绘图 落实
D．定义 定界 划界
4．④“政治地理学在边界问题上曾经经历过多次分类”到全文结束，说明了边界的分类即种类，下面边界分类的结构示意图比较合理的一项是
[ ]
科目：gzwl 来源： 题型：阅读理解
第一部分 力＆物体的平衡
第一讲 力的处理
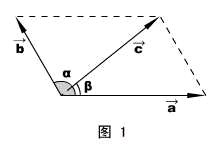
一、矢量的运算
1、加法
表达：
+ 
= 
。
名词：
为“和矢量”。
法则：平行四边形法则。如图1所示。
和矢量大小：c = 
，其中α为
和
的夹角。
和矢量方向：
在
、
之间，和
夹角β= arcsin
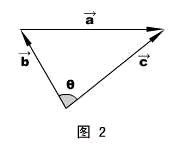
2、减法
表达：
= 
－
。
名词：
为“被减数矢量”，
为“减数矢量”，
为“差矢量”。
法则：三角形法则。如图2所示。将被减数矢量和减数矢量的起始端平移到一点，然后连接两时量末端，指向被减数时量的时量，即是差矢量。
差矢量大小：a = 
，其中θ为
和
的夹角。
差矢量的方向可以用正弦定理求得。
一条直线上的矢量运算是平行四边形和三角形法则的特例。
例题：已知质点做匀速率圆周运动，半径为R ，周期为T ，求它在
T内和在
T内的平均加速度大小。
解说：如图3所示，A到B点对应
T的过程，A到C点对应
T的过程。这三点的速度矢量分别设为
、
和
。
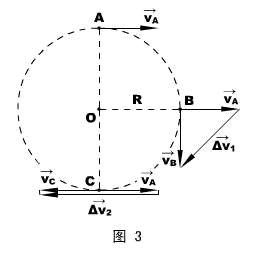
根据加速度的定义 
= 
得：
= 
，
= 
由于有两处涉及矢量减法，设两个差矢量 
= 
－
，
= 
－
，根据三角形法则，它们在图3中的大小、方向已绘出（
的“三角形”已被拉伸成一条直线）。
本题只关心各矢量的大小，显然：
= 
= 
= 
，且：
= 
= 
，
= 2
= 
所以：
= 
= 
= 
，
= 
= 
= 
。
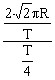（学生活动）观察与思考：这两个加速度是否相等，匀速率圆周运动是不是匀变速运动？
答：否；不是。
3、乘法
矢量的乘法有两种：叉乘和点乘，和代数的乘法有着质的不同。
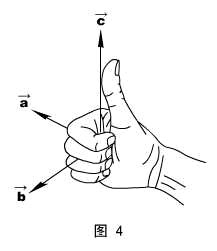
⑴ 叉乘
表达：
×
= 
名词：
称“矢量的叉积”，它是一个新的矢量。
叉积的大小：c = absinα，其中α为
和
的夹角。意义：
的大小对应由
和
作成的平行四边形的面积。
叉积的方向：垂直
和
确定的平面，并由右手螺旋定则确定方向，如图4所示。
显然，
×
≠
×
，但有：
×
= －
×
⑵ 点乘
表达：
·
= c
名词：c称“矢量的点积”，它不再是一个矢量，而是一个标量。
点积的大小：c = abcosα，其中α为
和
的夹角。
二、共点力的合成
1、平行四边形法则与矢量表达式
2、一般平行四边形的合力与分力的求法
余弦定理（或分割成RtΔ）解合力的大小
正弦定理解方向
三、力的分解
1、按效果分解
2、按需要——正交分解
第二讲 物体的平衡
一、共点力平衡
1、特征：质心无加速度。
2、条件：Σ
= 0 ，或 
= 0 ，
= 0
例题：如图5所示，长为L 、粗细不均匀的横杆被两根轻绳水平悬挂，绳子与水平方向的夹角在图上已标示，求横杆的重心位置。
解说：直接用三力共点的知识解题，几何关系比较简单。
答案：距棒的左端L/4处。
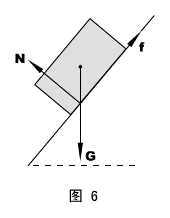
（学生活动）思考：放在斜面上的均质长方体，按实际情况分析受力，斜面的支持力会通过长方体的重心吗？
解：将各处的支持力归纳成一个N ，则长方体受三个力（G 、f 、N）必共点，由此推知，N不可能通过长方体的重心。正确受力情形如图6所示（通常的受力图是将受力物体看成一个点，这时，N就过重心了）。
答：不会。
二、转动平衡
1、特征：物体无转动加速度。
2、条件：Σ
= 0 ，或ΣM+ =ΣM-
如果物体静止，肯定会同时满足两种平衡，因此用两种思路均可解题。
3、非共点力的合成
大小和方向：遵从一条直线矢量合成法则。
作用点：先假定一个等效作用点，然后让所有的平行力对这个作用点的和力矩为零。
第三讲 习题课
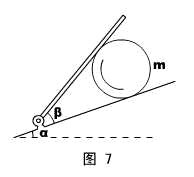
1、如图7所示，在固定的、倾角为α斜面上，有一块可以转动的夹板（β不定），夹板和斜面夹着一个质量为m的光滑均质球体，试求：β取何值时，夹板对球的弹力最小。
解说：法一，平行四边形动态处理。
对球体进行受力分析，然后对平行四边形中的矢量G和N1进行平移，使它们构成一个三角形，如图8的左图和中图所示。
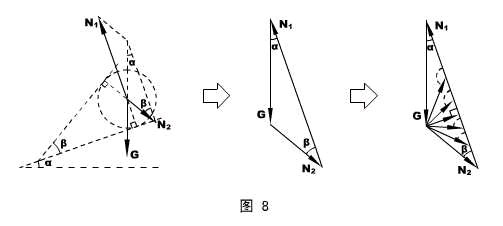
由于G的大小和方向均不变，而N1的方向不可变，当β增大导致N2的方向改变时，N2的变化和N1的方向变化如图8的右图所示。
显然，随着β增大，N1单调减小，而N2的大小先减小后增大，当N2垂直N1时，N2取极小值，且N2min = Gsinα。
法二，函数法。
看图8的中间图，对这个三角形用正弦定理，有：
= 
，即：N2 = 
，β在0到180°之间取值，N2的极值讨论是很容易的。
答案：当β= 90°时，甲板的弹力最小。
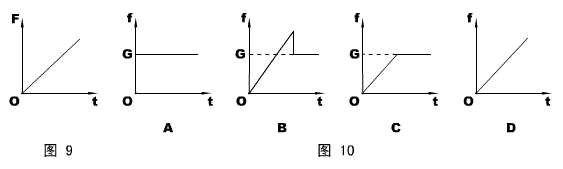
2、把一个重为G的物体用一个水平推力F压在竖直的足够高的墙壁上，F随时间t的变化规律如图9所示，则在t = 0开始物体所受的摩擦力f的变化图线是图10中的哪一个？
解说：静力学旨在解决静态问题和准静态过程的问题，但本题是一个例外。物体在竖直方向的运动先加速后减速，平衡方程不再适用。如何避开牛顿第二定律，是本题授课时的难点。
静力学的知识，本题在于区分两种摩擦的不同判据。
水平方向合力为零，得：支持力N持续增大。
物体在运动时，滑动摩擦力f = μN ，必持续增大。但物体在静止后静摩擦力f′≡ G ，与N没有关系。
对运动过程加以分析，物体必有加速和减速两个过程。据物理常识，加速时，f ＜ G ，而在减速时f ＞ G 。
答案：B 。
3、如图11所示，一个重量为G的小球套在竖直放置的、半径为R的光滑大环上，另一轻质弹簧的劲度系数为k ，自由长度为L（L＜2R），一端固定在大圆环的顶点A ，另一端与小球相连。环静止平衡时位于大环上的B点。试求弹簧与竖直方向的夹角θ。
解说：平行四边形的三个矢量总是可以平移到一个三角形中去讨论，解三角形的典型思路有三种：①分割成直角三角形（或本来就是直角三角形）；②利用正、余弦定理；③利用力学矢量三角形和某空间位置三角形相似。本题旨在贯彻第三种思路。
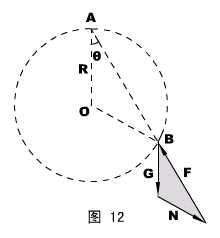
分析小球受力→矢量平移，如图12所示，其中F表示弹簧弹力，N表示大环的支持力。
（学生活动）思考：支持力N可不可以沿图12中的反方向？（正交分解看水平方向平衡——不可以。）
容易判断，图中的灰色矢量三角形和空间位置三角形ΔAOB是相似的，所以：
⑴
由胡克定律：F = k（
- R） ⑵
几何关系：
= 2Rcosθ ⑶
解以上三式即可。
答案：arccos
。
（学生活动）思考：若将弹簧换成劲度系数k′较大的弹簧，其它条件不变，则弹簧弹力怎么变？环的支持力怎么变？
答：变小；不变。
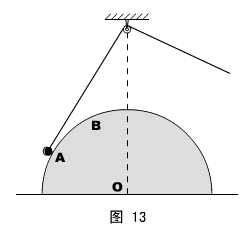
（学生活动）反馈练习：光滑半球固定在水平面上，球心O的正上方有一定滑轮，一根轻绳跨过滑轮将一小球从图13所示的A位置开始缓慢拉至B位置。试判断：在此过程中，绳子的拉力T和球面支持力N怎样变化？
解：和上题完全相同。
答：T变小，N不变。
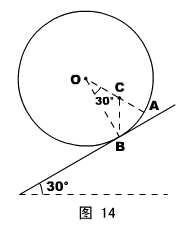
4、如图14所示，一个半径为R的非均质圆球，其重心不在球心O点，先将它置于水平地面上，平衡时球面上的A点和地面接触；再将它置于倾角为30°的粗糙斜面上，平衡时球面上的B点与斜面接触，已知A到B的圆心角也为30°。试求球体的重心C到球心O的距离。
解说：练习三力共点的应用。
根据在平面上的平衡，可知重心C在OA连线上。根据在斜面上的平衡，支持力、重力和静摩擦力共点，可以画出重心的具体位置。几何计算比较简单。
答案：
R 。
（学生活动）反馈练习：静摩擦足够，将长为a 、厚为b的砖块码在倾角为θ的斜面上，最多能码多少块？
解：三力共点知识应用。
答：
。
4、两根等长的细线，一端拴在同一悬点O上，另一端各系一个小球，两球的质量分别为m1和m2 ，已知两球间存在大小相等、方向相反的斥力而使两线张开一定角度，分别为45和30°，如图15所示。则m1 : m2为多少？
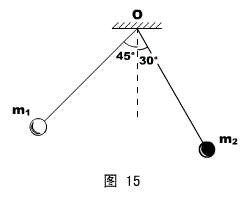
解说：本题考查正弦定理、或力矩平衡解静力学问题。
对两球进行受力分析，并进行矢量平移，如图16所示。
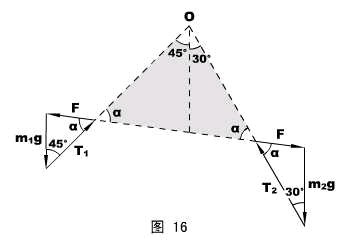
首先注意，图16中的灰色三角形是等腰三角形，两底角相等，设为α。
而且，两球相互作用的斥力方向相反，大小相等，可用同一字母表示，设为F 。
对左边的矢量三角形用正弦定理，有：
= 
①
同理，对右边的矢量三角形，有：
= 
②
解①②两式即可。
答案：1 ：
。
（学生活动）思考：解本题是否还有其它的方法？
答：有——将模型看成用轻杆连成的两小球，而将O点看成转轴，两球的重力对O的力矩必然是平衡的。这种方法更直接、简便。
应用：若原题中绳长不等，而是l1 ：l2 = 3 ：2 ，其它条件不变，m1与m2的比值又将是多少？
解：此时用共点力平衡更加复杂（多一个正弦定理方程），而用力矩平衡则几乎和“思考”完全相同。
答：2 ：3
。
5、如图17所示，一个半径为R的均质金属球上固定着一根长为L的轻质细杆，细杆的左端用铰链与墙壁相连，球下边垫上一块木板后，细杆恰好水平，而木板下面是光滑的水平面。由于金属球和木板之间有摩擦（已知摩擦因素为μ），所以要将木板从球下面向右抽出时，至少需要大小为F的水平拉力。试问：现要将木板继续向左插进一些，至少需要多大的水平推力？
解说：这是一个典型的力矩平衡的例题。
以球和杆为对象，研究其对转轴O的转动平衡，设木板拉出时给球体的摩擦力为f ，支持力为N ，重力为G ，力矩平衡方程为：
f R + N（R + L）= G（R + L） ①
球和板已相对滑动，故：f = μN ②
解①②可得：f = 
再看木板的平衡，F = f 。
同理，木板插进去时，球体和木板之间的摩擦f′= 
= F′。
答案：
。
第四讲 摩擦角及其它
一、摩擦角
1、全反力：接触面给物体的摩擦力与支持力的合力称全反力，一般用R表示，亦称接触反力。
2、摩擦角：全反力与支持力的最大夹角称摩擦角，一般用φm表示。
此时，要么物体已经滑动，必有：φm = arctgμ（μ为动摩擦因素），称动摩擦力角；要么物体达到最大运动趋势，必有：φms = arctgμs（μs为静摩擦因素），称静摩擦角。通常处理为φm = φms 。
3、引入全反力和摩擦角的意义：使分析处理物体受力时更方便、更简捷。
二、隔离法与整体法
1、隔离法：当物体对象有两个或两个以上时，有必要各个击破，逐个讲每个个体隔离开来分析处理，称隔离法。
在处理各隔离方程之间的联系时，应注意相互作用力的大小和方向关系。
2、整体法：当各个体均处于平衡状态时，我们可以不顾个体的差异而讲多个对象看成一个整体进行分析处理，称整体法。
应用整体法时应注意“系统”、“内力”和“外力”的涵义。
三、应用
1、物体放在水平面上，用与水平方向成30°的力拉物体时，物体匀速前进。若此力大小不变，改为沿水平方向拉物体，物体仍能匀速前进，求物体与水平面之间的动摩擦因素μ。
解说：这是一个能显示摩擦角解题优越性的题目。可以通过不同解法的比较让学生留下深刻印象。
法一，正交分解。（学生分析受力→列方程→得结果。）
法二，用摩擦角解题。
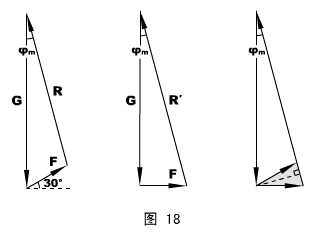
引进全反力R ，对物体两个平衡状态进行受力分析，再进行矢量平移，得到图18中的左图和中间图（注意：重力G是不变的，而全反力R的方向不变、F的大小不变），φm指摩擦角。
再将两图重叠成图18的右图。由于灰色的三角形是一个顶角为30°的等腰三角形，其顶角的角平分线必垂直底边……故有：φm = 15°。
最后，μ= tgφm 。
答案：0.268 。
（学生活动）思考：如果F的大小是可以选择的，那么能维持物体匀速前进的最小F值是多少？
解：见图18，右图中虚线的长度即Fmin ，所以，Fmin = Gsinφm 。
答：Gsin15°（其中G为物体的重量）。
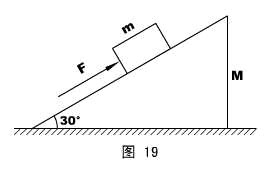
2、如图19所示，质量m = 5kg的物体置于一粗糙斜面上，并用一平行斜面的、大小F = 30N的推力推物体，使物体能够沿斜面向上匀速运动，而斜面体始终静止。已知斜面的质量M = 10kg ，倾角为30°，重力加速度g = 10m/s2 ，求地面对斜面体的摩擦力大小。
解说：
本题旨在显示整体法的解题的优越性。
法一，隔离法。简要介绍……
法二，整体法。注意，滑块和斜面随有相对运动，但从平衡的角度看，它们是完全等价的，可以看成一个整体。
做整体的受力分析时，内力不加考虑。受力分析比较简单，列水平方向平衡方程很容易解地面摩擦力。
答案：26.0N 。
（学生活动）地面给斜面体的支持力是多少？
解：略。
答：135N 。
应用：如图20所示，一上表面粗糙的斜面体上放在光滑的水平地面上，斜面的倾角为θ。另一质量为m的滑块恰好能沿斜面匀速下滑。若用一推力F作用在滑块上，使之能沿斜面匀速上滑，且要求斜面体静止不动，就必须施加一个大小为P = 4mgsinθcosθ的水平推力作用于斜面体。使满足题意的这个F的大小和方向。
解说：这是一道难度较大的静力学题，可以动用一切可能的工具解题。
法一：隔离法。
由第一个物理情景易得，斜面于滑块的摩擦因素μ= tgθ
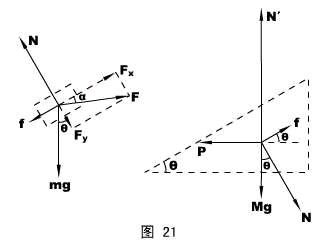
对第二个物理情景，分别隔离滑块和斜面体分析受力，并将F沿斜面、垂直斜面分解成Fx和Fy ，滑块与斜面之间的两对相互作用力只用两个字母表示（N表示正压力和弹力，f表示摩擦力），如图21所示。
对滑块，我们可以考查沿斜面方向和垂直斜面方向的平衡——
Fx = f + mgsinθ
Fy + mgcosθ= N
且 f = μN = Ntgθ
综合以上三式得到：
Fx = Fytgθ+ 2mgsinθ ①
对斜面体，只看水平方向平衡就行了——
P = fcosθ+ Nsinθ
即：4mgsinθcosθ=μNcosθ+ Nsinθ
代入μ值，化简得：Fy = mgcosθ ②
②代入①可得：Fx = 3mgsinθ
最后由F =
解F的大小，由tgα= 
解F的方向（设α为F和斜面的夹角）。
答案：大小为F = mg
，方向和斜面夹角α= arctg(
)指向斜面内部。
法二：引入摩擦角和整体法观念。
仍然沿用“法一”中关于F的方向设置（见图21中的α角）。
先看整体的水平方向平衡，有：Fcos(θ- α) = P ⑴
再隔离滑块，分析受力时引进全反力R和摩擦角φ，由于简化后只有三个力（R、mg和F），可以将矢量平移后构成一个三角形，如图22所示。
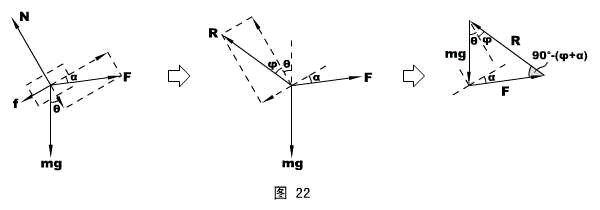
在图22右边的矢量三角形中，有：
= 
= 
⑵
注意：φ= arctgμ= arctg(tgθ) = θ ⑶
解⑴⑵⑶式可得F和α的值。
