
科目:czsx 来源:2013-2014学年北京市密云九年级上学期期末考试数学试卷(解析版) 题型:解答题
已知:如图,Rt△ABC中,CD是斜边AB上的高.求证:AC2=AD·AB

科目:czsx 来源:模拟题 题型:解答题
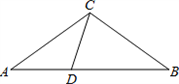
科目:czsx 来源:2008年北京市宣武区中考数学二模试卷(解析版) 题型:解答题
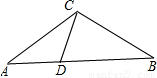
科目:czsx 来源: 题型:解答题
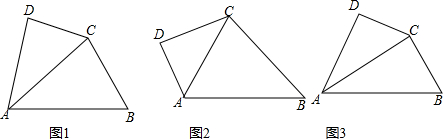
科目:czsx 来源: 题型:
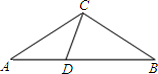 已知:如图,在△ABC中,D为AB边上一点,∠A=36°,AC=BC,AC2=AB•AD.
已知:如图,在△ABC中,D为AB边上一点,∠A=36°,AC=BC,AC2=AB•AD.科目:czsx 来源: 题型:解答题
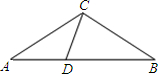 已知:如图,在△ABC中,D为AB边上一点,∠A=36°,AC=BC,AC2=AB•AD.
已知:如图,在△ABC中,D为AB边上一点,∠A=36°,AC=BC,AC2=AB•AD.科目:czsx 来源:2011年上海市黄浦区光明初中九年级复习数学试卷(解析版) 题型:解答题
 AB.
AB.
科目:czsx 来源:2008年上海市闸北区中考数学一模试卷(解析版) 题型:解答题
