3.(1)自主阅读:如图1,AD∥BC,连接AB、AC、BD、CD,则S
△ABC=S
△BCD.
证明:分别过点A和D,作AF⊥BC,DE⊥BC,由AD∥BC,可得AF=DE.
又因为S
△ABC=$\frac{1}{2}×BC×AF$,S
△BCD=$\frac{1}{2}×BC×DE$
所以S
△ABC=S
△BCD由此我们可以得到以下的结论:像图1这样,同底等高的三角形面积相等.
(2)结论应用:如果一条直线(线段)把一个平面图形的面积分成相等的两部分,我们把这条直线(线段)称为这个平面图形的一条面积等分线(段).如三角形的一条中线就是三角形的一条面积等分线段;平行四边形的一条对角线就是平行四边形的一条面积等分线段.
小明通过研究,发现过四边形的某一顶点的直线可以将该四边形平分为面积相等的两部分.
他画出了如下示意图(如图2),得到了符合要求的直线AF.
小明的作图步骤如下:
第一步:连结AC;
第二步:过点B作BE∥AC交DC的延长线于点E;
第三步:取ED中点F,作直线AF;
则直线AF即为所求.
请你帮小明写出该作法的验证过程:
(3)类比发现:请参考小明思考问题的方法,解决问题:
如图3,五边形ABOCD,各顶点坐标为:A(3,4),B(0,2),O(0,0),C(4,0),D(4,2).请你构造一条经过顶点A的直线,将五边形ABOCD分为面积相等的两部分,并求出该直线对应的函数表达式.
(4)提出问题:
结合下面所给的情景,请自主创设一个问题并给以解释:
如图4,C是线段AB上任意一点,分别以AC、BC为边在线段AB同侧构造等边三角形△ACD和等边三角形△CBE,若△CBE的面积是1cm
2.
【问题】求△EBD的面积.


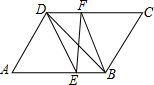 如图,在平行四边形ABCD中,DE,BF分别是∠ADC,∠ABC的角平分线,分别交AB,CD于点E,F.
如图,在平行四边形ABCD中,DE,BF分别是∠ADC,∠ABC的角平分线,分别交AB,CD于点E,F.

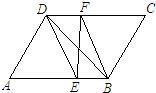 17、如图,在平行四边形ABCD中,DE,BF分别是∠ADC,∠ABC的角平分线,分别交AB,CD于点E,F.
17、如图,在平行四边形ABCD中,DE,BF分别是∠ADC,∠ABC的角平分线,分别交AB,CD于点E,F.