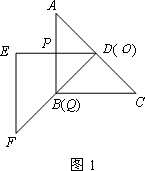如图.将两块直角三角板的直角顶点C叠放在一起答案解析
科目:czsx
来源:
题型:
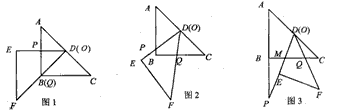
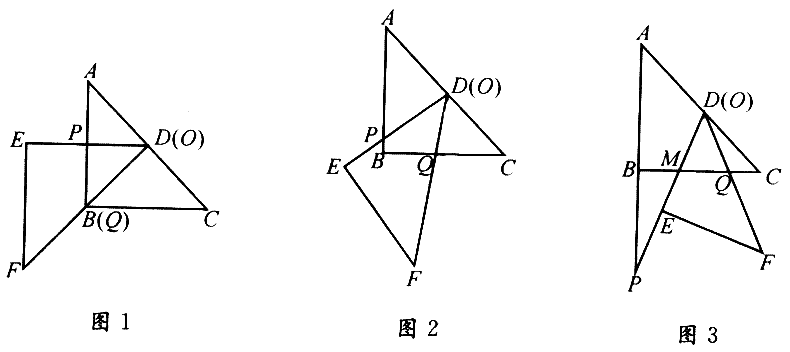
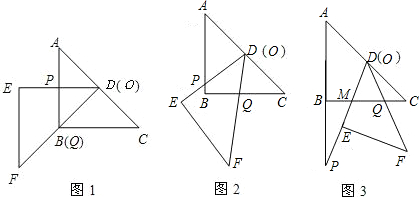
把两块全等的直角三角形ABC和DEF叠放在一起,使三角板DEF的锐角顶点D与三角板ABC的斜边中点O重合,其中∠ABC=∠DEF=90°,∠C=∠F=45°,AB=DE=4,把三角板ABC固定不动,让三角板DEF绕点O旋转,设射线DE与射线AB相交于点P,射线DF与线段BC相交于点Q.
(1)如图1,当射线DF经过点B,即点Q与点B重合时,易证△APD∽△CDQ.此时,AP•CQ=
;
(2)将三角板DEF由图1所示的位置绕点O沿逆时针方向旋转,设旋转角为α.其中0°<α<90°,问AP•CQ的值是否改变?说明你的理由;
(3)在(2)的条件下,设CQ=x,两块三角板重叠面积为y,求y与x的函数关系式.(图2,图3供解题用)
查看答案和解析>>
科目:czsx
来源:
题型:
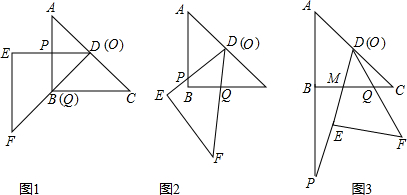
把两块全等的直角三角形ABC和DEF叠放在一起,使三角板DEF的锐角顶点D与三角板ABC的斜边中点O重合,其中∠ABC=∠DEF=90°,∠C=∠F=45°,AB=DE=4,把三角板ABC固定不动,让三角板DEF绕点O旋转,设射线DE与射线AB相交于点P,射线DF与线段BC相交于点Q.
(1)如图1,当射线DF经过点B,即点Q与点B重合时,易证△APD∽△CDQ.此时,AP•CQ
=8
=8
.
(2)将三角板DEF由图1所示的位置绕点O沿逆时针方向旋转,设旋转角为α.其中0°<α<90°,问AP•CQ的值是否改变?说明你的理由.
(3)在(2)的条件下,设CQ=x,两块三角板重叠面积为y,求y与x的函数关系式.(图2,图3供解题用)
查看答案和解析>>
科目:czsx
来源:
题型:
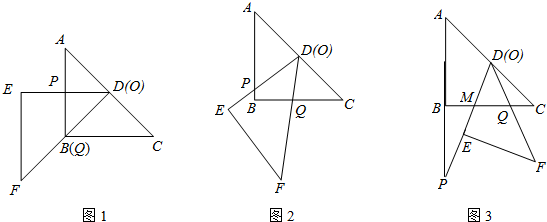
把两块全等的直角三角形ABC和DEF叠放在一起,使三角板DEF的锐角顶点D与三角板ABC的斜边中点O重合,其中∠ABC=∠DEF=90°,∠C=∠F=45°,AB=DE=4,把三角板ABC固定不动,让三角板DEF绕点O旋转,设射线DE与射线AB相交于点P,射线DF与线段BC相交于点Q.
(1)如图,当射线DF经过点B,即点Q与点B重合时,易证△APD∽△CDQ.此时,AP•CQ=
8
8
.
(2)将三角板DEF由图所示的位置绕点O沿逆时针方向旋转,设旋转角为α.其中0°<α<90°,问AP•CQ的值是否改变?说明你的理由.
(3)在(2)的条件下,设2<x<4,两块三角板重叠面积为y,求y与x的函数关系式.
(图2,图3供解题用)
查看答案和解析>>
科目:czsx
来源:
题型:
把两块全等的直角三角形ABC和DEF叠放在一起,使三角板DEF的锐角顶点D与三角板ABC的斜边中点O重合,其中∠ABC=∠DEF=90°,∠C=∠F=45°,AB=DE=4,把三角板ABC固定不动,让三角板DEF绕点O旋转,设射线DE与射线AB相交于点P,射线DF与线段BC相交于点Q.
(1)如图1,当射线DF经过点B,即点Q与点B重合时,易证△APD∽△CDQ.此时AP•CQ的值为
8
8
.将三角板DEF由图1所示的位置绕点O沿逆时针方向旋转,设旋转角为α.其中0°<α<90°,则AP•CQ的值是否会改变?
答:
不会
不会
.(填“会”或“不会”)此时AP•CQ的值为
8
8
.(不必说明理由)
(2)在(1)的条件下,设CQ=x,两块三角板重叠面积为y,求y与x的函数关系式.(图2、图3供解题用)
(3)在(1)的条件下,PQ能否与AC平行?若能,求出y的值;若不能,试说明理由.

查看答案和解析>>
科目:czsx
来源:2006年山东省常德市初中毕业生学业考试数学试卷
题型:044
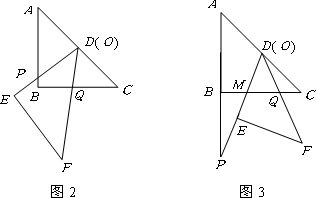
把两块全等的直角三角形ABC和DEF叠放在一起,使三角板DEF的锐角顶点D与三角板ABC的斜边中点O重合,其中∠ABC=∠DEF=90°,∠C=∠F=45°,AB=DE=4,把三角板ABC固定不动,让三角板DEF绕点O旋转,设射线DE与射线AB相交于点P,射线DF与线段BC相交于点Q.
(1)如图1,当射线DF经过点B,即点Q与点B重合时,易证△APD∽△CDQ.此时,AP·CQ=_________.
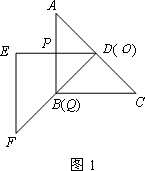
(2)将三角板DEF由图1所示的位置绕点O沿逆时针方向旋转,设旋转角为α.其中0°<α<90°,问AP·CQ的值是否改变?说明你的理由.
(3)在(2)的条件下,设CQ=x,两块三角板重叠面积为y,求y与x的函数关系式.(图2,图3供解题用)
查看答案和解析>>
科目:czsx
来源:2006年湖南省常德市初中毕业生学业考试数学试卷
题型:059
把两块全等的直角三角形ABC和DEF叠放在一起,使三角板DEF的锐角顶点D与三角板ABC的斜边中点O重合,其中∠ABC=∠DEF=90°,∠C=∠F=45°,AB=DE=4,把三角板ABC固定不动,让三角板DEF绕点O旋转,设射线DE与射线AB相交于点P,射线DF与线段BC相交于点Q.
(1)如下图,当射线DF经过点B,即点Q与点B重合时,易证△APD∽△CDQ.此时,AP·CQ=_________.

(2)将三角板DEF由上图所示的位置绕点O沿逆时针方向旋转,设旋转角为α.其中0°<α<90°,问AP·CQ的值是否改变?说明你的理由.
(3)在(2)的条件下,设CQ=x,两块三角板重叠面积为y,求y与x的函数关系式.(图1,图2供解题用)

查看答案和解析>>
科目:czsx
来源:
题型:解答题
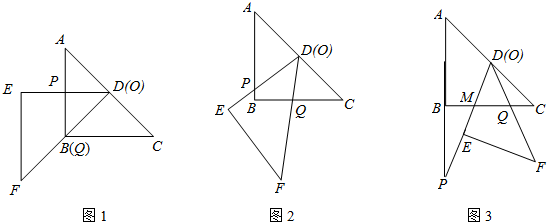
把两块全等的直角三角形ABC和DEF叠放在一起,使三角板DEF的锐角顶点D与三角板ABC的斜边中点O重合,其中∠ABC=∠DEF=90°,∠C=∠F=45°,AB=DE=4,把三角板ABC固定不动,让三角板DEF绕点O旋转,设射线DE与射线AB相交于点P,射线DF与线段BC相交于点Q.
(1)如图,当射线DF经过点B,即点Q与点B重合时,易证△APD∽△CDQ.此时,AP•CQ=______.
(2)将三角板DEF由图所示的位置绕点O沿逆时针方向旋转,设旋转角为α.其中0°<α<90°,问AP•CQ的值是否改变?说明你的理由.
(3)在(2)的条件下,设2<x<4,两块三角板重叠面积为y,求y与x的函数关系式.
(图2,图3供解题用)
查看答案和解析>>
科目:czsx
来源:
题型:解答题
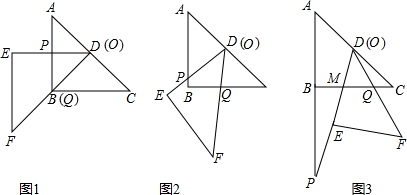
把两块全等的直角三角形ABC和DEF叠放在一起,使三角板DEF的锐角顶点D与三角板ABC的斜边中点O重合,其中∠ABC=∠DEF=90°,∠C=∠F=45°,AB=DE=4,把三角板ABC固定不动,让三角板DEF绕点O旋转,设射线DE与射线AB相交于点P,射线DF与线段BC相交于点Q.
(1)如图1,当射线DF经过点B,即点Q与点B重合时,易证△APD∽△CDQ.此时AP•CQ的值为______.将三角板DEF由图1所示的位置绕点O沿逆时针方向旋转,设旋转角为α.其中0°<α<90°,则AP•CQ的值是否会改变?
答:______.(填“会”或“不会”)此时AP•CQ的值为______.(不必说明理由)
(2)在(1)的条件下,设CQ=x,两块三角板重叠面积为y,求y与x的函数关系式.(图2、图3供解题用)
(3)在(1)的条件下,PQ能否与AC平行?若能,求出y的值;若不能,试说明理由.
查看答案和解析>>
科目:czsx
来源:江苏期末题
题型:解答题
把两块全等的直角三角形ABC和DEF叠放在一起,使三角板DEF的锐角顶点D与三角扳ABC的斜边中点O重合,其中∠ABC=∠DEF=90°,∠C=∠F=45°,AB=DE=4,把三角板ABC固定不动,让三角扳DEF绕点O旋转,设射线DE与射线AB相交于点P,射线DF与线段BC相交于点Q。
(1)如图1,当射线DF经过点B,即点Q与点B重合时,易证△APD~△CDQ。此时,AP·CQ=______。
(2)将三角板DEF由图1所示的位置绕点O沿逆时针方向旋转,设旋转角为a.其中 0°<a<90°,问AP·CQ的值是否改变?说明你的理由。
(3)在(2)的条件下,设CQ=x,两块三角板重叠面积为y,求y与x的函数关系式。(图2,图3供解题用)
查看答案和解析>>
科目:czsx
来源:重庆市模拟题
题型:解答题
把两块全等的直角三角形ABC和DEF 叠放在一起,使三角板DEF的锐角顶点D与三角板ABC的斜边中点O 重合,其中∠ABC=∠DEF=90。,∠C=∠F=45。,AB=DE=4把三角板ABC固定不动,让三角板DEF绕点O旋转,设射线DE与射线AB相交于点P,射线DF与线段BC相交于点Q。
(1)如图1,当射线DF经过点B,即点Q与点B重合时,易证△APD∽△CDQ,此时AP﹒CQ的值为( )。将三角板DEF由图1所示的位置绕点O沿逆时针方向旋转,设旋转角为α。 其中0。<α<90。 ,则 AP﹒CQ的值是否会改变?答:( )(填“会”或“不会”)此时AP﹒CQ的值为( )(不必说明理由)
(2)在(1)的条件下,设CQ=x,两块三角板重叠面积为y,求y与x的函数关系式.(图2、图3供解题用)
(3)在(1)的条件下,PQ能否与AC平行?若能,求出y的值;若不能,试说明理由。
查看答案和解析>>
科目:czsx
来源:第27章《相似》中考题集(31):27.2 相似三角形(解析版)
题型:解答题
把两块全等的直角三角形ABC和DEF叠放在一起,使三角板DEF的锐角顶点D与三角板ABC的斜边中点O重合,其中∠ABC=∠DEF=90°,∠C=∠F=45°,AB=DE=4,把三角板ABC固定不动,让三角板DEF绕点O旋转,设射线DE与射线AB相交于点P,射线DF与线段BC相交于点Q.
(1)如图1,当射线DF经过点B,即点Q与点B重合时,易证△APD∽△CDQ.此时,AP•CQ=______;
(2)将三角板DEF由图1所示的位置绕点O沿逆时针方向旋转,设旋转角为α.其中0°<α<90°,问AP•CQ的值是否改变?说明你的理由;
(3)在(2)的条件下,设CQ=x,两块三角板重叠面积为y,求y与x的函数关系式.(图2,图3供解题用)

查看答案和解析>>
科目:czsx
来源:2009-2010学年湖南省怀化三中九年级(上)期末数学试卷(解析版)
题型:解答题
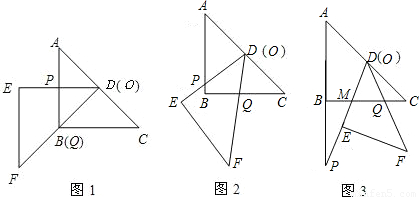
把两块全等的直角三角形ABC和DEF叠放在一起,使三角板DEF的锐角顶点D与三角板ABC的斜边中点O重合,其中∠ABC=∠DEF=90°,∠C=∠F=45°,AB=DE=4,把三角板ABC固定不动,让三角板DEF绕点O旋转,设射线DE与射线AB相交于点P,射线DF与线段BC相交于点Q.
(1)如图1,当射线DF经过点B,即点Q与点B重合时,易证△APD∽△CDQ.此时,AP•CQ=______;
(2)将三角板DEF由图1所示的位置绕点O沿逆时针方向旋转,设旋转角为α.其中0°<α<90°,问AP•CQ的值是否改变?说明你的理由;
(3)在(2)的条件下,设CQ=x,两块三角板重叠面积为y,求y与x的函数关系式.(图2,图3供解题用)
查看答案和解析>>
科目:czsx
来源:第19章《相似形》常考题集(14):19.6 相似三角形的性质(解析版)
题型:解答题
把两块全等的直角三角形ABC和DEF叠放在一起,使三角板DEF的锐角顶点D与三角板ABC的斜边中点O重合,其中∠ABC=∠DEF=90°,∠C=∠F=45°,AB=DE=4,把三角板ABC固定不动,让三角板DEF绕点O旋转,设射线DE与射线AB相交于点P,射线DF与线段BC相交于点Q.
(1)如图1,当射线DF经过点B,即点Q与点B重合时,易证△APD∽△CDQ.此时,AP•CQ=______;
(2)将三角板DEF由图1所示的位置绕点O沿逆时针方向旋转,设旋转角为α.其中0°<α<90°,问AP•CQ的值是否改变?说明你的理由;
(3)在(2)的条件下,设CQ=x,两块三角板重叠面积为y,求y与x的函数关系式.(图2,图3供解题用)

查看答案和解析>>
科目:czsx
来源:第19章《相似形》中考题集(18):19.6 相似三角形的性质(解析版)
题型:解答题
把两块全等的直角三角形ABC和DEF叠放在一起,使三角板DEF的锐角顶点D与三角板ABC的斜边中点O重合,其中∠ABC=∠DEF=90°,∠C=∠F=45°,AB=DE=4,把三角板ABC固定不动,让三角板DEF绕点O旋转,设射线DE与射线AB相交于点P,射线DF与线段BC相交于点Q.
(1)如图1,当射线DF经过点B,即点Q与点B重合时,易证△APD∽△CDQ.此时,AP•CQ=______;
(2)将三角板DEF由图1所示的位置绕点O沿逆时针方向旋转,设旋转角为α.其中0°<α<90°,问AP•CQ的值是否改变?说明你的理由;
(3)在(2)的条件下,设CQ=x,两块三角板重叠面积为y,求y与x的函数关系式.(图2,图3供解题用)

查看答案和解析>>
科目:czsx
来源:第29章《相似形》中考题集(22):29.5 相似三角形的性质(解析版)
题型:解答题
把两块全等的直角三角形ABC和DEF叠放在一起,使三角板DEF的锐角顶点D与三角板ABC的斜边中点O重合,其中∠ABC=∠DEF=90°,∠C=∠F=45°,AB=DE=4,把三角板ABC固定不动,让三角板DEF绕点O旋转,设射线DE与射线AB相交于点P,射线DF与线段BC相交于点Q.
(1)如图1,当射线DF经过点B,即点Q与点B重合时,易证△APD∽△CDQ.此时,AP•CQ=______;
(2)将三角板DEF由图1所示的位置绕点O沿逆时针方向旋转,设旋转角为α.其中0°<α<90°,问AP•CQ的值是否改变?说明你的理由;
(3)在(2)的条件下,设CQ=x,两块三角板重叠面积为y,求y与x的函数关系式.(图2,图3供解题用)

查看答案和解析>>
科目:czsx
来源:第29章《相似形》常考题集(13):29.5 相似三角形的性质(解析版)
题型:解答题
把两块全等的直角三角形ABC和DEF叠放在一起,使三角板DEF的锐角顶点D与三角板ABC的斜边中点O重合,其中∠ABC=∠DEF=90°,∠C=∠F=45°,AB=DE=4,把三角板ABC固定不动,让三角板DEF绕点O旋转,设射线DE与射线AB相交于点P,射线DF与线段BC相交于点Q.
(1)如图1,当射线DF经过点B,即点Q与点B重合时,易证△APD∽△CDQ.此时,AP•CQ=______;
(2)将三角板DEF由图1所示的位置绕点O沿逆时针方向旋转,设旋转角为α.其中0°<α<90°,问AP•CQ的值是否改变?说明你的理由;
(3)在(2)的条件下,设CQ=x,两块三角板重叠面积为y,求y与x的函数关系式.(图2,图3供解题用)

查看答案和解析>>
科目:czsx
来源:第3章《图形的相似》常考题集(15):3.3 相似三角形的性质和判定(解析版)
题型:解答题
把两块全等的直角三角形ABC和DEF叠放在一起,使三角板DEF的锐角顶点D与三角板ABC的斜边中点O重合,其中∠ABC=∠DEF=90°,∠C=∠F=45°,AB=DE=4,把三角板ABC固定不动,让三角板DEF绕点O旋转,设射线DE与射线AB相交于点P,射线DF与线段BC相交于点Q.
(1)如图1,当射线DF经过点B,即点Q与点B重合时,易证△APD∽△CDQ.此时,AP•CQ=______;
(2)将三角板DEF由图1所示的位置绕点O沿逆时针方向旋转,设旋转角为α.其中0°<α<90°,问AP•CQ的值是否改变?说明你的理由;
(3)在(2)的条件下,设CQ=x,两块三角板重叠面积为y,求y与x的函数关系式.(图2,图3供解题用)

查看答案和解析>>
科目:czsx
来源:第3章《图形的相似》中考题集(21):3.3 相似三角形的性质和判定(解析版)
题型:解答题
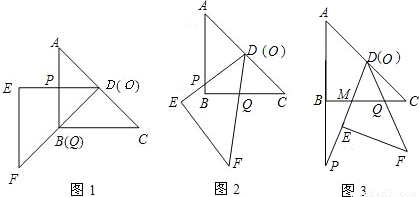
把两块全等的直角三角形ABC和DEF叠放在一起,使三角板DEF的锐角顶点D与三角板ABC的斜边中点O重合,其中∠ABC=∠DEF=90°,∠C=∠F=45°,AB=DE=4,把三角板ABC固定不动,让三角板DEF绕点O旋转,设射线DE与射线AB相交于点P,射线DF与线段BC相交于点Q.
(1)如图1,当射线DF经过点B,即点Q与点B重合时,易证△APD∽△CDQ.此时,AP•CQ=______;
(2)将三角板DEF由图1所示的位置绕点O沿逆时针方向旋转,设旋转角为α.其中0°<α<90°,问AP•CQ的值是否改变?说明你的理由;
(3)在(2)的条件下,设CQ=x,两块三角板重叠面积为y,求y与x的函数关系式.(图2,图3供解题用)
查看答案和解析>>
科目:czsx
来源:第24章《图形的相似》中考题集(20):24.3 相似三角形(解析版)
题型:解答题
把两块全等的直角三角形ABC和DEF叠放在一起,使三角板DEF的锐角顶点D与三角板ABC的斜边中点O重合,其中∠ABC=∠DEF=90°,∠C=∠F=45°,AB=DE=4,把三角板ABC固定不动,让三角板DEF绕点O旋转,设射线DE与射线AB相交于点P,射线DF与线段BC相交于点Q.
(1)如图1,当射线DF经过点B,即点Q与点B重合时,易证△APD∽△CDQ.此时,AP•CQ=______;
(2)将三角板DEF由图1所示的位置绕点O沿逆时针方向旋转,设旋转角为α.其中0°<α<90°,问AP•CQ的值是否改变?说明你的理由;
(3)在(2)的条件下,设CQ=x,两块三角板重叠面积为y,求y与x的函数关系式.(图2,图3供解题用)

查看答案和解析>>
科目:czsx
来源:第24章《图形的相似》常考题集(15):24.3 相似三角形(解析版)
题型:解答题
把两块全等的直角三角形ABC和DEF叠放在一起,使三角板DEF的锐角顶点D与三角板ABC的斜边中点O重合,其中∠ABC=∠DEF=90°,∠C=∠F=45°,AB=DE=4,把三角板ABC固定不动,让三角板DEF绕点O旋转,设射线DE与射线AB相交于点P,射线DF与线段BC相交于点Q.
(1)如图1,当射线DF经过点B,即点Q与点B重合时,易证△APD∽△CDQ.此时,AP•CQ=______;
(2)将三角板DEF由图1所示的位置绕点O沿逆时针方向旋转,设旋转角为α.其中0°<α<90°,问AP•CQ的值是否改变?说明你的理由;
(3)在(2)的条件下,设CQ=x,两块三角板重叠面积为y,求y与x的函数关系式.(图2,图3供解题用)

查看答案和解析>>