科目:czsx 来源: 题型:
 |
| MN |
 |
| MQ |
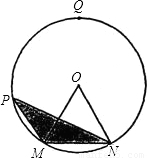
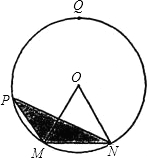 除外)上运动,设点P到弦MN的距离为x,△OMN的面积是S.
除外)上运动,设点P到弦MN的距离为x,△OMN的面积是S.科目:czsx 来源: 题型:
 ,
,科目:czsx 来源: 题型:
 点.动点Q从点P出发,沿射线PC方向以2cm/s的速度运动,以P为圆心,PQ长为半径作圆.设点Q运动的时间为t s.
点.动点Q从点P出发,沿射线PC方向以2cm/s的速度运动,以P为圆心,PQ长为半径作圆.设点Q运动的时间为t s.科目:czsx 来源: 题型:
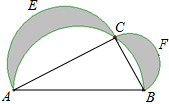 如图,在以AB为直径的半圆上取一点C,分别以AC、BC为直径在△ABC外作半圆AEC和BFC.当C点在什么位置上时,图中两个弯月形AEC和BFC的面积之和最大?
如图,在以AB为直径的半圆上取一点C,分别以AC、BC为直径在△ABC外作半圆AEC和BFC.当C点在什么位置上时,图中两个弯月形AEC和BFC的面积之和最大?科目:czsx 来源:新课标3维同步训练与评价数学 九年级(下) 题型:044
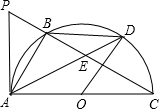
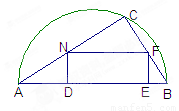
如图,在直径为AB的圆内,划出一块三角形区域使三角形的一边为AB,顶点C在半圆上,其他两边分别为6和8,现在建造一个内接内△ABC的矩形水池DEFN,其中DE在AB上,如图的设计方案是AC=8,BC=6.
?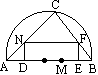
(1)求△ABC中AB边上的高h;
(2)设DN=x,当x为何值时,水池DEFN的面积最大?
(3)实施施工时,发现在AB边上距B点1.85m处的M处有一棵大树,这棵大树是否位于最大矩形水池的边上?如果在,为保护大树,请设计出另外的方案,使内接于满足条件的三角形中欲建的最大矩形水池能避开这棵大树.
科目:czsx 来源: 题型:
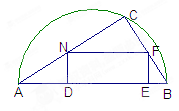
如图,在直径为AB的一块半圆形土地上,画出一块三角形区域,使三角形的一边为AB,顶点C在半圆上,其它两边长分别为6cm和8cm,现要建造一个内接于△ABC的矩形水池DEFN,其中DE在AB上,如图所示的设计方案是使AC=8cm,BC=6cm。
(1)求△ABC中AB边上的高h;
(2)设DN=x,当x取何值时,水池DEFN的面积最大?
(3)实际施工时,发现在AB上距B点1.85m处有一棵大树,则这棵大树是否位于最大矩形的边上?如果在,为了保护大树,请你设计出另外的方案,使内接于满足条件的三角形中建最大矩形水池能避开大树。
科目:czsx 来源: 题型:
科目:czsx 来源:2012届江苏省沭阳银河学校九年级下学期质量检测数学卷 题型:解答题
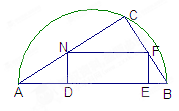
如图,在直径为AB的一块半圆形土地上,画出一块三角形区域,使三角形的一边为AB,顶点C在半圆上,其它两边长分别为6cm和8cm,现要建造一个内接于△ABC的矩形水池DEFN,其中DE在AB上,如图所示的设计方案是使AC=8cm,BC=6cm。
(1)求△ABC中AB边上的高h;
(2)设DN=x,当x取何值时,水池DEFN的面积最大?
(3)实际施工时,发现在AB上距B点1.85m处有一棵大树,则这棵大树是否位于最大矩形的边上?如果在,为了保护大树,请你设计出另外的方案,使内接于满足条件的三角形中建最大矩形水池能避开大树。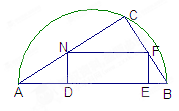
科目:czsx 来源:2011-2012学年江苏省九年级下学期质量检测数学卷 题型:解答题
如图,在直径为AB的一块半圆形土地上,画出一块三角形区域,使三角形的一边为AB,顶点C在半圆上,其它两边长分别为6cm和8cm,现要建造一个内接于△ABC的矩形水池DEFN,其中DE在AB上,如图所示的设计方案是使AC=8cm,BC=6cm。
(1)求△ABC中AB边上的高h;
(2)设DN=x,当x取何值时,水池DEFN的面积最大?
(3)实际施工时,发现在AB上距B点1.85m处有一棵大树,则这棵大树是否位于最大矩形的边上?如果在,为了保护大树,请你设计出另外的方案,使内接于满足条件的三角形中建最大矩形水池能避开大树。
科目:czsx 来源:2011-2012年天津市南开区九年级第一学期期中考试数学卷 题型:选择题
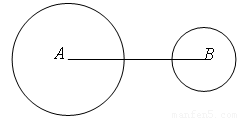
如图, 的半径分别为
的半径分别为 ,且
,且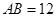 ,若做一
,若做一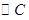 使得三圆的圆心在同一直线上,且
使得三圆的圆心在同一直线上,且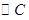 与
与 外切,
外切,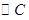 与
与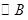 相交于两点,则
相交于两点,则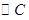 的半径可能是()
的半径可能是()
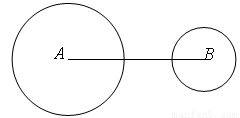
(A)3 (B)4 (C)5 (D)6
科目:czsx 来源:2012届天津市南开区九年级上学期期中检测数学试卷 题型:选择题
如图,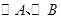 的半径分别为
的半径分别为 ,且
,且 ,若做一
,若做一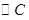 使得三圆的圆心在同一直线上,且
使得三圆的圆心在同一直线上,且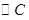 与
与 外切,
外切,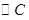 与
与 相交于两点,则
相交于两点,则 的半径可能是()
的半径可能是()
(A)3 (B)4 (C)5 (D)6
科目:czsx 来源: 题型:解答题
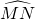 的中点,圆心角∠MON=60°,点P在
的中点,圆心角∠MON=60°,点P在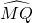 (M点
(M点 除外)上运动,设点P到弦MN的距离为x,△OMN的面积是S.
除外)上运动,设点P到弦MN的距离为x,△OMN的面积是S.科目:czsx 来源: 题型:解答题
 ,
,科目:czsx 来源: 题型:解答题
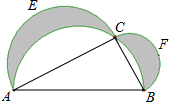 如图,在以AB为直径的半圆上取一点C,分别以AC、BC为直径在△ABC外作半圆AEC和BFC.当C点在什么位置上时,图中两个弯月形AEC和BFC的面积之和最大?
如图,在以AB为直径的半圆上取一点C,分别以AC、BC为直径在△ABC外作半圆AEC和BFC.当C点在什么位置上时,图中两个弯月形AEC和BFC的面积之和最大?科目:czsx 来源:第3章《圆》中考题集(19):3.1 圆(解析版) 题型:解答题
 的中点,圆心角∠MON=60°,点P在
的中点,圆心角∠MON=60°,点P在 (M点除外)上运动,设点P到弦MN的距离为x,△OMN的面积是S.
(M点除外)上运动,设点P到弦MN的距离为x,△OMN的面积是S.
科目:czsx 来源:第28章《圆》中考题集(19):28.1 圆的认识(解析版) 题型:解答题
 的中点,圆心角∠MON=60°,点P在
的中点,圆心角∠MON=60°,点P在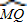 (M点除外)上运动,设点P到弦MN的距离为x,△OMN的面积是S.
(M点除外)上运动,设点P到弦MN的距离为x,△OMN的面积是S.
科目:czsx 来源:第3章《圆》中考题集(08):3.2 圆的对称性(解析版) 题型:解答题
 的中点,圆心角∠MON=60°,点P在
的中点,圆心角∠MON=60°,点P在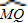 (M点除外)上运动,设点P到弦MN的距离为x,△OMN的面积是S.
(M点除外)上运动,设点P到弦MN的距离为x,△OMN的面积是S.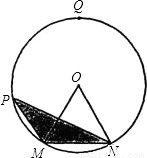
科目:czsx 来源:第22章《圆(上)》中考题集(11):22.3 圆的对称性(解析版) 题型:解答题
 的中点,圆心角∠MON=60°,点P在
的中点,圆心角∠MON=60°,点P在 (M点除外)上运动,设点P到弦MN的距离为x,△OMN的面积是S.
(M点除外)上运动,设点P到弦MN的距离为x,△OMN的面积是S.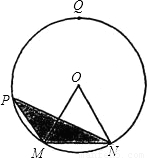
科目:czsx 来源:第27章《圆(一)》中考题集(06):27.1 圆的基本概念和性质(解析版) 题型:解答题
 的中点,圆心角∠MON=60°,点P在
的中点,圆心角∠MON=60°,点P在 (M点除外)上运动,设点P到弦MN的距离为x,△OMN的面积是S.
(M点除外)上运动,设点P到弦MN的距离为x,△OMN的面积是S.
科目:czsx 来源:第5章《中心对称图形(二)》中考题集(07):5.2 圆的对称性(解析版) 题型:解答题
 的中点,圆心角∠MON=60°,点P在
的中点,圆心角∠MON=60°,点P在 (M点除外)上运动,设点P到弦MN的距离为x,△OMN的面积是S.
(M点除外)上运动,设点P到弦MN的距离为x,△OMN的面积是S.