
科目:czsx 来源: 题型:
 如图,已知直线AB经过点C(1,2),与x轴、y轴分别交于A点、B点,CD⊥x轴于D,CE⊥y轴于E,CF与x轴交于F.
如图,已知直线AB经过点C(1,2),与x轴、y轴分别交于A点、B点,CD⊥x轴于D,CE⊥y轴于E,CF与x轴交于F.科目:czsx 来源: 题型:解答题
 如图,已知直线AB经过点C(1,2),与x轴、y轴分别交于A点、B点,CD⊥x轴于D,CE⊥y轴于E,CF与x轴交于F.
如图,已知直线AB经过点C(1,2),与x轴、y轴分别交于A点、B点,CD⊥x轴于D,CE⊥y轴于E,CF与x轴交于F.科目:czsx 来源:北京期末题 题型:解答题
 时,求直线AB的解析式;
时,求直线AB的解析式; ,当直线AB绕点C旋转到使FC⊥AB时,求BC的长;
,当直线AB绕点C旋转到使FC⊥AB时,求BC的长; (F、O、G的对应点分别为
(F、O、G的对应点分别为 ),把
),把 沿x轴正方向平移到使得点
沿x轴正方向平移到使得点 与点A重合,设在平移过程中
与点A重合,设在平移过程中 与四边形CDOE重叠的面积为y,
与四边形CDOE重叠的面积为y, 的长为x,求y与x的函数关系式及自变量x的取值范围。
的长为x,求y与x的函数关系式及自变量x的取值范围。
科目:czsx 来源:2005-2006学年北京市海淀区上地实验中学九年级(上)期末数学试卷(解析版) 题型:解答题

科目:czsx 来源:2005-2006学年北京市海淀区九年级(上)期末数学试卷(解析版) 题型:解答题

科目:czsx 来源: 题型:
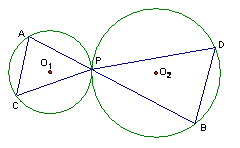
已知如图:⊙O1与⊙O2外切于点P, 直线AB经过点P交⊙O1于A,交⊙O2于B,点C、D分别为⊙O1、⊙O2上的点,且∠ACP=65°,则∠BDP= 。
科目:czsx 来源: 题型:
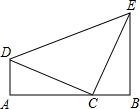 为A、B,试说明AC=BE的理由.
为A、B,试说明AC=BE的理由.
|
科目:czsx 来源: 题型:填空题
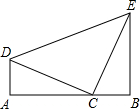 为A、B,试说明AC=BE的理由.
为A、B,试说明AC=BE的理由.
科目:czsx 来源: 题型:
 已知:如图,在△CDE中,∠DCE=90°,CD=CE,直线AB经过点C,且点D、E在直线AB的同侧,在直线AB上点C的左、右两侧分别取点A、B,使得∠DAC=∠EBC=∠DCE.
已知:如图,在△CDE中,∠DCE=90°,CD=CE,直线AB经过点C,且点D、E在直线AB的同侧,在直线AB上点C的左、右两侧分别取点A、B,使得∠DAC=∠EBC=∠DCE.科目:czsx 来源: 题型:解答题
 合),过点P分别向x轴、y轴作垂线,垂足分别为C、D.设OC=x,四边形OCPD的面积为S.
合),过点P分别向x轴、y轴作垂线,垂足分别为C、D.设OC=x,四边形OCPD的面积为S. 时,S有最大值
时,S有最大值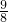 ,求直线AB的解析式;
,求直线AB的解析式;科目:czsx 来源:2012年北京市顺义区中考数学二模试卷(解析版) 题型:解答题
 时,S有最大值
时,S有最大值 ,求直线AB的解析式;
,求直线AB的解析式;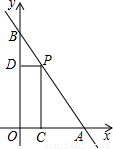
科目:czsx 来源:2016年初中毕业升学考试(湖北襄阳卷)数学(解析版) 题型:解答题
如图,直线AB经过⊙O上的点C,直线AO与⊙O交于点E和点D,OB与OD交于点F,连接DF,DC.已知OA=OB,CA=CB,DE=10,DF=6.

(1)求证:①直线AB是⊙O的切线;②∠FDC=∠EDC;
(2)求CD的长.