
科目:czsx 来源:101网校同步练习 初二数学 人教版(新课标2004年初审) 人教版(新课标2004年初审) 题型:013
如图所示,在△ABC中,∠C=90°,点O为△ABC的三条角平分线的交点,OD⊥BC,OE⊥AC,OF⊥AB,点D、E、F分别是垂足,且AB=10,BC=8,CA=6,则点O到三边AB、AC、BC的距离分别是

A.2,2,2
B.3,3,3
C.4,3,2
D.2,3,5
科目:czsx 来源: 题型:
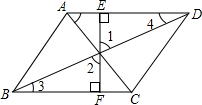 下面是小明作业中对一道题的解答以及老师的批阅
下面是小明作业中对一道题的解答以及老师的批阅科目:czsx 来源: 题型:解答题
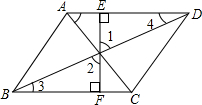 下面是小明作业中对一道题的解答以及老师的批阅
下面是小明作业中对一道题的解答以及老师的批阅科目:czsx 来源: 题型:解答题
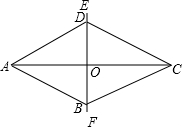 12m和16m,小明设计了下列方案,如图所示.
12m和16m,小明设计了下列方案,如图所示.科目:czsx 来源:不详 题型:解答题

科目:czsx 来源:同步题 题型:解答题

科目:czsx 来源: 题型:
 51、园林工人打算在人民公园里设计一个菱形的花坛,要求使菱形两条对角线的长分别为12m和16m,小明设计了下列方案,如图所示.
51、园林工人打算在人民公园里设计一个菱形的花坛,要求使菱形两条对角线的长分别为12m和16m,小明设计了下列方案,如图所示.