已知a为函数f（x）=x3–12x的极小值点，则a=

（A）–4 （B）–2 （C）4 （D）2

已知函数f(x)＝ax³＋bx²＋cx在x＝±1处取得极值，且在x＝0处的切线的斜率为－3.

(1)求f(x)的解析式；

(2)若过点A(2，m)可作曲线y＝f(x)的三条切线，求实数m的取值范围．

【解析】本试题主要考查了导数在研究函数中的运用。第一问，利用函数f(x)＝ax³＋bx²＋cx在x＝±1处取得极值，且在x＝0处的切线的斜率为－3，得到c＝－3　∴a＝1, f(x)＝x³－3x

(2)中设切点为(x₀，x₀³－3x₀)，因为过点A(2，m)，所以∴m－(x₀³－3x₀)＝(3x₀²－3)(2－x₀)分离参数∴m＝－2x₀³＋6x₀²－6

然后利用g(x)＝－2x³＋6x²－6函数求导数，判定单调性，从而得到要是有三解，则需要满足－6<m<2

解：(1)f′(x)＝3ax²＋2bx＋c

依题意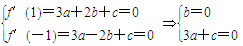

又f′(0)＝－3

∴c＝－3　∴a＝1　∴f(x)＝x³－3x

(2)设切点为(x₀，x₀³－3x₀)，

∵f′(x)＝3x²－3，∴f′(x₀)＝3x₀²－3

∴切线方程为y－(x₀³－3x₀)＝(3x₀²－3)(x－x₀)

又切线过点A(2，m)

∴m－(x₀³－3x₀)＝(3x₀²－3)(2－x₀)

∴m＝－2x₀³＋6x₀²－6

令g(x)＝－2x³＋6x²－6

则g′(x)＝－6x²＋12x＝－6x(x－2)

由g′(x)＝0得x＝0或x＝2

∴g(x)在(－∞，0)单调递减，(0,2)单调递增，(2，＋∞)单调递减．

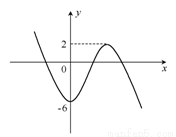
∴g(x)_极小值＝g(0)＝－6，g(x)_极大值＝g(2)＝2

画出草图知，当－6<m<2时，m＝－2x³＋6x²－6有三解，

所以m的取值范围是(－6,2)．

设函数f（x）=x³-12x，则下列结论正确的是

1. A.
   函数f（x）在（-∞，-1）上单调递增
2. B.
   函数f（x）的极小值是-12
3. C.
   函数f（x）的图象与直线y=10只有一个公共点
4. D.
   函数f（x）的图象在点（-2，f（-2））处的切线方程为y=16